[译]Rich feature hierarchies for accurate object detection and semantic segmentation
R-CNN(Regions with CNN features, 具有CNN特征的区域)是早期最先在目标检测领域中使用卷积神经网络的模型之一,其结合了图像处理、机器学习和深度学习,在当时达到了非常好的结果
原文地址:Rich feature hierarchies for accurate object detection and semantic segmentation
Abstract
摘要
Object detection performance, as measured on the canonical PASCAL VOC dataset, has plateaued in the last few years. The best-performing methods are complex ensemble systems that typically combine multiple low-level image features with high-level context. In this paper, we propose a simple and scalable detection algorithm that improves mean average precision (mAP) by more than 30% relative to the previous best result on VOC 2012—achieving a mAP of 53.3%. Our approach combines two key insights: (1) one can apply high-capacity convolutional neural networks (CNNs) to bottom-up region proposals in order to localize and segment objects and (2) when labeled training data is scarce, supervised pre-training for an auxiliary task, followed by domain-specific fine-tuning, yields a significant performance boost. Since we combine region proposals with CNNs, we call our method R-CNN: Regions with CNN features. We also compare R-CNN to OverFeat, a recently proposed sliding-window detector based on a similar CNN architecture. We find that R-CNN outperforms OverFeat by a large margin on the 200-class ILSVRC2013 detection dataset. Source code for the complete system is available at http://www.cs.berkeley.edu/˜rbg/rcnn.
在典型的PASCAL-VOC数据集上测得的目标检测性能在过去几年中趋于平稳。表现最好的方法是复杂的集成系统,通常将多个低级图像特征与高级上下文结合起来。在本文中,我们提出了一种简单且可扩展的检测算法,与之前VOC 2012的最佳结果相比,平均精度(mAP)提高了30%以上,mAP达到了53.3%。我们的方法结合了两个关键的见解:(1)可以将高容量卷积神经网络(CNNs)应用到自下而上的区域建议中,以便定位和分割对象;(2)当标记的训练数据稀少时,监督辅助任务的预训练,然后进行特定领域的微调,带来显著的性能提升。由于我们将区域建议与CNN结合起来,我们称之为R-CNN方法:具有CNN特征的区域。我们还将R-CNN与OverFeat进行了比较,OverFeat是最近提出的一种基于类似CNN架构的滑动窗口检测器。我们发现,在200类ILSVRC2013检测数据集上,R-CNN的性能大大优于OverFeat。完整系统的源代码位于https://github.com/rbgirshick/rcnn(Caffe+Matlib版本)
Introduction
引言
Features matter. The last decade of progress on various visual recognition tasks has been based considerably on the use of SIFT [29] and HOG [7]. But if we look at performance on the canonical visual recognition task, PASCAL VOC object detection [15], it is generally acknowledged that progress has been slow during 2010-2012, with small gains obtained by building ensemble systems and employing minor variants of successful methods.
特征很重要。在过去的十年中,各种视觉识别任务的进展很大程度上是基于SIFT[29]和HOG[7]的使用。但是,如果我们看看标准视觉识别任务PASCAL VOC目标检测的性能[15],人们普遍认为,2010-2012年期间进展缓慢,通过构建集成系统和采用已成功方法的微小变体获得的收益很小
SIFT and HOG are blockwise orientation histograms, a representation we could associate roughly with complex cells in V1, the first cortical area in the primate visual pathway. But we also know that recognition occurs several stages downstream, which suggests that there might be hierarchical, multi-stage processes for computing features that are even more informative for visual recognition.
SIFT和HOG是块方向的直方图,我们可以粗略地将其与灵长类视觉通路的第一个皮层V1中的复杂细胞联系起来。但我们也知道,识别发生在下游的几个阶段,这意味着可能有层次化的、多阶段的过程来计算特征,这些过程对于视觉识别的信息量更大
Fukushima’s "neocognitron" [19], a biologically-inspired hierarchical and shift-invariant model for pattern recognition, was an early attempt at just such a process. The neocognitron, however, lacked a supervised training algorithm. Building on Rumelhart et al. [33], LeCun et al. [26] showed that stochastic gradient descent via backpropagation was effective for training convolutional neural networks (CNNs), a class of models that extend the neocognitron.
Fukushima的“neocognitron”[19]是一种基于生物启发的层次和平移不变的模式识别模型,是对这一过程的早期尝试。然而,neocognitron缺乏一种有监督的训练算法。建立在Rumelhart等人[33]的基础上,LeCun等人[26]的结果表明通过反向传播的随机梯度下降对于训练卷积神经网络(CNNs)是有效的
CNNs saw heavy use in the 1990s (e.g., [27]), but then fell out of fashion with the rise of support vector machines. In 2012, Krizhevsky et al. [25] rekindled interest in CNNs by showing substantially higher image classification accuracy on the ImageNet Large Scale Visual Recognition Challenge (ILSVRC) [9, 10]. Their success resulted from training a large CNN on 1.2 million labeled images, together with a few twists on LeCun’s CNN (e.g.,
rectifying non-linearities and “dropout” regularization).
CNNs在20世纪90年代得到了广泛的应用(如[27]),但随后随着支持向量机的兴起而过时。2012年,Krizhevsky等人[25]通过在ImageNet大规模视觉识别挑战(ILSVRC)上显示更高的图像分类精度,重新燃起了人们对CNN的兴趣[9,10]。他们的成功来自于在120万张标签图片上训练一个大型CNN,以及在LeCun的CNN上的一些调整(例如使用
The significance of the ImageNet result was vigorously debated during the ILSVRC 2012 workshop. The central issue can be distilled to the following: To what extent do the CNN classification results on ImageNet generalize to object detection results on the PASCAL VOC Challenge?
ImageNet结果的重要性在ILSVRC 2012研讨会期间受到了激烈的争论。核心问题可以归结为以下几个方面:ImageNet上的CNN分类结果可以在多大程度上泛化到PASCAL VOC挑战下的目标检测结果?
We answer this question by bridging the gap between image classification and object detection. This paper is the first to show that a CNN can lead to dramatically higher object detection performance on PASCAL VOC as compared to systems based on simpler HOG-like features. To achieve this result, we focused on two problems: localizing objects with a deep network and training a high-capacity model with only a small quantity of annotated detection data.
我们通过缩小图像分类和目标检测之间的差距来回答这个问题。本文首次表明,与基于简单HOG-like特征的系统相比,CNN可以显著提高PASCAL-VOC上的目标检测性能。为了达到这一目的,我们重点研究了两个问题:利用深度网络定位目标和利用少量带标注的检测数据训练高容量模型
Unlike image classification, detection requires localizing (likely many) objects within an image. One approach frames localization as a regression problem. However, work from Szegedy et al. [38], concurrent with our own, indicates that this strategy may not fare well in practice (they report a mAP of 30.5% on VOC 2007 compared to the 58.5% achieved by our method). An alternative is to build a sliding-window detector. CNNs have been used in this way for at least two decades, typically on constrained object categories, such as faces [32, 40] and pedestrians [35]. In order to maintain high spatial resolution, these CNNs typically only have two convolutional and pooling layers. We also considered adopting a sliding-window approach. However, units high up in our network, which has five convolutional layers, have very large receptive fields (195 × 195 pixels) and strides (32×32 pixels) in the input image, which makes precise localization within the sliding-window paradigm an open technical challenge.
与图像分类不同,检测需要在图像中定位(可能是许多)对象。一种方法是将定位作为一个回归问题。然而,Szegedy等人的工作[38]与我们的一致,表明这一策略在实践中可能效果不佳(他们报告的VOC 2007年的mAP为30.5%,而我们的方法实现的mAP为58.5%)。另一种方法是建立一个滑动窗口检测器。为了保持较高的空间分辨率,这些CNN通常只有两个卷积层和池化层。我们也考虑采用滑动窗口方法。然而,在我们的网络中,具有五个卷积层的单元在输入图像中具有非常大的感受野(195×195像素)和步长(32×32像素),这使得在滑动窗口模式中的精确定位成为一个公开的技术挑战
Instead, we solve the CNN localization problem by operating within the “recognition using regions” paradigm [21], which has been successful for both object detection [39] and semantic segmentation [5]. At test time, our method generates around 2000 category-independent region proposals for the input image, extracts a fixed-length feature vector from each proposal using a CNN, and then classifies each region with category-specific linear SVMs. We use a simple technique (affine image warping) to compute a fixed-size CNN input from each region proposal, regardless of the region’s shape. Figure 1 presents an overview of our method and highlights some of our results. Since our system combines region proposals with CNNs, we dub the method R-CNN: Regions with CNN features.
相反,我们通过在“使用区域的识别”范例[21]内操作来解决CNN定位问题,该范例在目标检测[39]和语义分割[5]方面都取得了成功。在测试时,我们的方法为输入图像生成大约2000个类别无关的区域建议,使用CNN从每个建议中提取一个固定长度的特征向量,然后使用类别特定的线性支持向量机对每个区域进行分类。我们使用一种简单的技术(仿射图像扭曲)来计算来自每个区域建议的固定大小的CNN输入,而不管该区域的形状如何。由于我们的系统将区域建议与CNNs结合起来,因此我们将R-CNN方法称为具有CNN特征的区域
In this updated version of this paper, we provide a head-to-head comparison of R-CNN and the recently proposed OverFeat [34] detection system by running R-CNN on the 200-class ILSVRC2013 detection dataset. OverFeat uses a sliding-window CNN for detection and until now was the best performing method on ILSVRC2013 detection. We show that R-CNN significantly outperforms OverFeat, with a mAP of 31.4% versus 24.3%.
在本文的更新版本中,我们通过在200类ILSVRC2013检测数据集上运行R-CNN,对R-CNN和最近提出的OverFeat[34]检测系统进行了比较。OverFeat使用滑动窗口CNN进行检测,迄今为止是ILSVRC2013检测中性能最好的方法。我们显示R-CNN的表现明显优于OverFeat,mAP为31.4%对24.3%
A second challenge faced in detection is that labeled data is scarce and the amount currently available is insufficient for training a large CNN. The conventional solution to this problem is to use unsupervised pre-training, followed by supervised fine-tuning (e.g., [35]). The second principle contribution of this paper is to show that supervised pre-training on a large auxiliary dataset (ILSVRC), followed by domainspecific fine-tuning on a small dataset (PASCAL), is an effective paradigm for learning high-capacity CNNs when data is scarce. In our experiments, fine-tuning for detection improves mAP performance by 8 percentage points. After fine-tuning, our system achieves a mAP of 54% on VOC 2010 compared to 33% for the highly-tuned, HOG-based deformable part model (DPM) [17, 20]. We also point readers to contemporaneous work by Donahue et al. [12], who show that Krizhevsky’s CNN can be used (without finetuning) as a blackbox feature extractor, yielding excellent performance on several recognition tasks including scene classification, fine-grained sub-categorization, and domain adaptation.
在检测中面临的第二个挑战是,标记数据是稀缺的,目前可用的数量不足以训练一个大型CNN。这个问题的传统解决方案是使用无监督的预训练,然后是有监督的微调(例如,[35])。本文的第二个主要贡献是,在一个大的辅助数据集(ILSVRC)上进行监督预训练,然后在特定的小数据集(PASCAL)上进行特定领域的微调,是在数据稀少的情况下学习高容量CNN的有效范例。在我们的实验中,对检测进行微调可以将mAP性能提高8个百分点。经过微调后,我们的系统在VOC 2010上实现了54% mAP,相比之下,高度调整后的基于HOG的可变形零件模型(DPM)仅实现了33% mAP[17,20]。我们还将读者介绍同期Donahue等人[12]的作品,他们发现Krizhevsky的CNN可以(无需微调)用作黑盒特征提取器,在包括场景分类、细粒度子分类和域自适应在内的多个识别任务中产生优异的性能
Our system is also quite efficient. The only class-specific computations are a reasonably small matrix-vector product and greedy non-maximum suppression. This computational property follows from features that are shared across all categories and that are also two orders of magnitude lower-dimensional than previously used region features (cf. [39]).
我们的系统也很有效率。唯一的特定类的计算是一个合理的小矩阵向量积和贪婪非最大抑制。这种计算特性来自于所有类别共享的特征,并且这些特征的维数比以前使用的区域特征低两个数量级(参见[39])
Understanding the failure modes of our approach is also critical for improving it, and so we report results from the detection analysis tool of Hoiem et al. [23]. As an immediate consequence of this analysis, we demonstrate that a simple bounding-box regression method significantly reduces mislocalizations, which are the dominant error mode.
了解该方法的失效模式对于改进该方法也至关重要,因此我们报告了Hoiem等人[23]的检测分析工具的结果。作为这一分析的直接结果,我们证明了一种简单的边界盒回归方法可以显著减少主要误差模式的错误定位
Before developing technical details, we note that because R-CNN operates on regions it is natural to extend it to the task of semantic segmentation. With minor modifications, we also achieve competitive results on the PASCAL VOC segmentation task, with an average segmentation accuracy of 47.9% on the VOC 2011 test set.
我们注意到由于R-CNN对区域进行操作,因此将其扩展到语义分割任务是很自然的。经过少量修改,我们在PASCAL VOC分割任务上也取得了有竞争力的结果,VOC 2011测试集的平均分割精度为47.9%
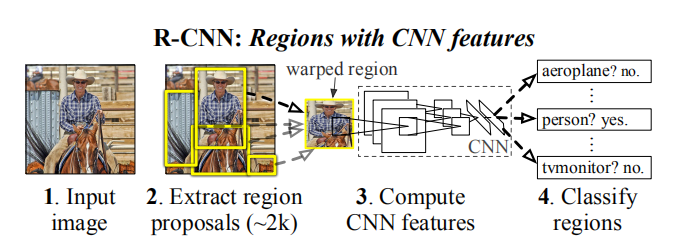
Figure 1: Object detection system overview. Our system (1) takes an input image, (2) extracts around 2000 bottom-up region proposals, (3) computes features for each proposal using a large convolutional neural network (CNN), and then (4) classifies each region using class-specific linear SVMs. R-CNN achieves a mean average precision (mAP) of 53.7% on PASCAL VOC 2010. For comparison, [39] reports 35.1% mAP using the same region proposals, but with a spatial pyramid and bag-of-visual-words approach. The popular deformable part models perform at 33.4%. On the 200-class ILSVRC2013 detection dataset, R-CNN’s mAP is 31.4%, a large improvement over OverFeat [34], which had the previous best result at 24.3%.
图1:目标检测系统概述。我们的系统(1)获取输入图像,(2)提取大约2000个自下而上的区域建议,(3)使用大型卷积神经网络(CNN)计算每个建议的特征,然后(4)使用类特定的线性SVM对每个区域进行分类。R-CNN在PASCAL VOC 2010上达到了53.7%的平均精度(mAP)。相比之下,论文[39]在使用相同的区域建议,但使用空间金字塔和视觉词袋方法下得到了35.1 mAP。流行的可变形零件模型的性能为33.4%。在200类ILSVRC2013检测数据集上,R-CNN的mAP为31.4%,比OverFeat[34]有很大的改进,OverFeat[34]之前的最佳结果为24.3%
Object detection with R-CNN
使用R-CNN的目标检测
Our object detection system consists of three modules. The first generates category-independent region proposals. These proposals define the set of candidate detections available to our detector. The second module is a large convolutional neural network that extracts a fixed-length feature vector from each region. The third module is a set of classspecific linear SVMs. In this section, we present our design decisions for each module, describe their test-time usage, detail how their parameters are learned, and show detection results on PASCAL VOC 2010-12 and on ILSVRC2013.
我们的目标检测系统由三个模块组成。首先生成类别独立的区域建议。这些建议定义了可供我们的检测器使用的候选检测集。第二个模块是一个大型卷积神经网络,它从每个区域提取一个固定长度的特征向量。第三个模块是一组类特定的线性支持向量机。在本节中,我们将介绍每个模块的设计决策,描述它们的测试时间使用,详细说明如何学习它们的参数,并在PASCAL VOC 2010-12和ILSVRC2013上显示检测结果
Module design
模块设计
Region proposals. A variety of recent papers offer methods for generating category-independent region proposals. Examples include: objectness [1], selective search [39], category-independent object proposals [14], constrained parametric min-cuts (CPMC) [5], multi-scale combinatorial grouping [3], and Cires¸an et al. [6], who detect mitotic cells by applying a CNN to regularly-spaced square crops, which are a special case of region proposals. While R-CNN is agnostic to the particular region proposal method, we use selective search to enable a controlled comparison with prior detection work (e.g., [39, 41]).
区域建议。最近的许多论文提供了生成类别独立区域建议的方法。示例包括:对象性[1]、选择性搜索[39]、与类别无关的目标建议[14]、约束参数最小割集(CPMC)[5]、多尺度组合分组[3]和Cires¸an等人[6]通过将CNN应用于规则间隔的方形作物来检测有丝分裂细胞(这是区域建议的一个特例)。虽然R-CNN不固定于特定的区域建议方法,但我们使用选择性搜索来保证能够和先前检测工作(例如,[39,41])进行比较
Feature extraction. We extract a 4096-dimensional feature vector from each region proposal using the Caffe [24] implementation of the CNN described by Krizhevsky et al. [25]. Features are computed by forward propagating a mean-subtracted 227 × 227 RGB image through five convolutional layers and two fully connected layers. We refer readers to [24, 25] for more network architecture details.
特征提取。我们使用Krizhevsky等人[25]描述的CNN的Caffe[24]实现从每个区域建议中提取4096维特征向量。特征通过将227×227 RGB图像输入五个卷积层和两个完全连接层来计算。我们请读者参考[24,25]了解更多的网络架构细节
In order to compute features for a region proposal, we must first convert the image data in that region into a form that is compatible with the CNN (its architecture requires inputs of a fixed 227 × 227 pixel size). Of the many possible transformations of our arbitrary-shaped regions, we opt for the simplest. Regardless of the size or aspect ratio of the candidate region, we warp all pixels in a tight bounding box around it to the required size. Prior to warping, we dilate the tight bounding box so that at the warped size there are exactly p pixels of warped image context around the original box (we use p = 16). Figure 2 shows a random sampling of warped training regions. Alternatives to warping are discussed in Appendix A.
为了计算区域建议的特征,我们必须首先将该区域中的图像数据转换为与CNN兼容的形式(其架构要求输入固定的227×227像素大小)。在任意形状区域的许多可能变换中,我们选择最简单的。无论候选区域的大小或宽高比如何,我们都会将其周围紧边界框中的所有像素扭曲为所需的大小。在扭曲之前,我们会展开紧边界框,以便在扭曲大小下,原始框周围正好有p个扭曲图像上下文像素(我们使用p=16)。图2显示了扭曲训练区域的随机抽样。附录A中讨论了扭曲的替代方案

Figure 2: Warped training samples from VOC 2007 train.
图2:来自VOC 2007训练集的扭曲训练样本
Test-time detection
At test time, we run selective search on the test image to extract around 2000 region proposals (we use selective search’s “fast mode” in all experiments). We warp each proposal and forward propagate it through the CNN in order to compute features. Then, for each class, we score each extracted feature vector using the SVM trained for that class. Given all scored regions in an image, we apply a greedy non-maximum suppression (for each class independently) that rejects a region if it has an intersection-over-union (IoU) overlap with a higher scoring selected region larger than a learned threshold.
在测试时,我们对测试图像运行选择性搜索以提取大约2000个区域建议(我们在所有实验中使用选择性搜索的“快速模式”)。我们扭曲每一个建议并通过CNN计算特征。然后,对于每一类,我们使用为该类训练的支持向量机对提取的特征向量进行评分。给定图像中的所有得分区域,我们应用一个贪婪非最大抑制(对于每一个独立的类),如果它与得分较高的选择区域的并集重叠上的交集比学习到的阈值高,则拒绝该区域
Run-time analysis. Two properties make detection efficient. First, all CNN parameters are shared across all categories. Second, the feature vectors computed by the CNN are low-dimensional when compared to other common approaches, such as spatial pyramids with bag-of-visual-word encodings. The features used in the UVA detection system [39], for example, are two orders of magnitude larger than ours (360k vs. 4k-dimensional).
运行时分析。两个特性使检测更有效。首先,所有CNN参数在所有类别中共享。其次,与其他常用方法相比(例如带有视觉文字编码包的空间金字塔),CNN计算出的特征向量是低维的。例如在UVA检测系统中使用的特征[39]比我们的大两个数量级(360k vs. 4k维)
The result of such sharing is that the time spent computing region proposals and features (13s/image on a GPU or 53s/image on a CPU) is amortized over all classes. The only class-specific computations are dot products between features and SVM weights and non-maximum suppression. In practice, all dot products for an image are batched into a single matrix-matrix product. The feature matrix is typically 2000×4096 and the SVM weight matrix is 4096×N, where N is the number of classes.
这种共享的结果是,计算区域建议和特征(GPU上的13s/图像或CPU上的53s/图像)所花费的时间在所有类中分摊。唯一的类具体计算是特征和SVM权重和非最大抑制之间的点积。实际上,图像的所有点积都被批处理成一个矩阵积。特征矩阵一般为2000×4096,支持向量机权重矩阵为4096×N,其中N为类数
This analysis shows that R-CNN can scale to thousands of object classes without resorting to approximate techniques, such as hashing. Even if there were 100k classes, the resulting matrix multiplication takes only 10 seconds on a modern multi-core CPU. This efficiency is not merely the result of using region proposals and shared features. The UVA system, due to its high-dimensional features, would be two orders of magnitude slower while requiring 134GB of memory just to store 100k linear predictors, compared to just 1.5GB for our lower-dimensional features.
该分析表明,R-CNN可以扩展到数千个对象类,而不诉诸近似技术,例如散列。即使有10万个类,在现代多核CPU上,矩阵乘法也只需要10秒。这种效率不仅仅是使用区域建议和共享特征的结果。由于其高维特性,UVA系统的速度将慢两个数量级,同时需要134GB的内存来存储100k个线性预测值,而我们的低维特征只需要1.5GB
It is also interesting to contrast R-CNN with the recent work from Dean et al. on scalable detection using DPMs and hashing [8]. They report a mAP of around 16% on VOC 2007 at a run-time of 5 minutes per image when introducing 10k distractor classes. With our approach, 10k detectors can run in about a minute on a CPU, and because no approximations are made mAP would remain at 59% (Section 3.2).
将R-CNN与Dean等人最近的研究进行对比也很有趣。关于使用DPMs和散列的可伸缩检测[8]。在测试10k个不同类别时,他们在VOC 2007上有大约16% mAP,每张图片的运行时间为5分钟。用我们的方法,10k检测器可以在CPU上运行大约一分钟,并且因为没有近似,mAP将保持在59%(第3.2节)
Training
训练
Supervised pre-training. We discriminatively pre-trained the CNN on a large auxiliary dataset (ILSVRC2012 classification) using image-level annotations only (bounding-box labels are not available for this data). Pre-training was performed using the open source Caffe CNN library [24]. In brief, our CNN nearly matches the performance of Krizhevsky et al. [25], obtaining a top-1 error rate 2.2 percentage points higher on the ILSVRC2012 classification validation set. This discrepancy is due to simplifications in the training process.
监督预训练。我们预先在一个大的辅助数据集(ILVRC2012分类)训练CNN模型,仅使用图像级别注释(边界框标签不可用于此数据)。使用开源Caffe CNN库进行了预训练[24]。简而言之,我们的CNN几乎与Krizhevsky等人[25]的表现相吻合。在ILSVRC2012分类验证集上获得top-1错误率2.2个百分点。这种差异是由于训练过程中的简化造成的
Domain-specific fine-tuning. To adapt our CNN to the new task (detection) and the new domain (warped proposal windows), we continue stochastic gradient descent (SGD) training of the CNN parameters using only warped region proposals. Aside from replacing the CNN’s ImageNet-specific 1000-way classification layer with a randomly initialized (N + 1)-way classification layer (where N is the number of object classes, plus 1 for background), the CNN architecture is unchanged. For VOC, N = 20 and for ILSVRC2013, N = 200. We treat all region proposals with ≥ 0.5 IoU overlap with a ground-truth box as positives for that box’s class and the rest as negatives. We start SGD at a learning rate of 0.001 (1/10th of the initial pre-training rate), which allows fine-tuning to make progress while not clobbering the initialization. In each SGD iteration, we uniformly sample 32 positive windows (over all classes) and 96 background windows to construct a mini-batch of size 128. We bias the sampling towards positive windows because they are extremely rare compared to background.
领域特定微调。为了使我们的CNN适应新任务(检测)和新领域(扭曲建议窗口),仅使用扭曲区域建议图片来继续通过随机梯度下降(SGD)训练CNN参数。除了用一个随机初始化的(N+1)大小的分类层(其中N是对象类的数量,加上1作为背景)替换CNN的ImageNet特定的1000方式分类层之外,CNN的架构没有改变。对于VOC,N=20;对于ILSVRC2013,N=200。我们将所有与先验框的IoU重叠度大于等于0.5的区域提案视为类的正样本,其余的则视为负样本。我们以0.001的学习率(初始预训练率的1/10)开始SGD,这允许微调在不破坏初始化的情况下取得进展。在每次SGD迭代中,我们都会统一采样32个正窗口(在所有类上)和96个背景窗口,以构造大小为128的小批量
Object category classifiers. Consider training a binary classifier to detect cars. It’s clear that an image region tightly enclosing a car should be a positive example. Similarly, it’s clear that a background region, which has nothing to do with cars, should be a negative example. Less clear is how to label a region that partially overlaps a car. We resolve this issue with an IoU overlap threshold, below which regions are defined as negatives. The overlap threshold, 0.3, was selected by a grid search over {0, 0.1, . . . , 0.5} on a validation set. We found that selecting this threshold carefully is important. Setting it to 0.5, as in [39], decreased mAP by 5 points. Similarly, setting it to 0 decreased mAP by 4 points. Positive examples are defined simply to be the ground-truth bounding boxes for each class.
对象类别分类器。考虑训练一个二值分类器来检测汽车。很明显,紧紧包围汽车的图像区域应该是一个正样本。同样很明显,与汽车无关的背景区域应该是一个负样本。不太清楚的是如何标记与汽车部分重叠的区域。我们用IoU重叠阈值来解决这个问题,低于这个阈值的区域被定义为负样本。重叠阈值0.3是通过在验证集上网格搜索{0, 0.1, . . . , 0.5}选定的。我们发现仔细选择这个阈值很重要。设置为0.5,如[39]所示,mAP减少了5个点。类似地,将其设置为0会使mAP减少4个点。正样本被定义为每个类的先验边界框
Once features are extracted and training labels are applied, we optimize one linear SVM per class. Since the training data is too large to fit in memory, we adopt the standard hard negative mining method [17, 37]. Hard negative mining converges quickly and in practice mAP stops increasing after only a single pass over all images.
一旦特征被提取和训练标签被应用,我们可以逐类优化线性支持向量机。由于训练数据太大,无法存储,我们采用标准负样本挖掘方法[17,37]。负样本挖掘收敛很快,在实际应用中,只需一次遍历所有图像,mAP就会停止增长
In Appendix B we discuss why the positive and negative examples are defined differently in fine-tuning versus SVM training. We also discuss the trade-offs involved in training detection SVMs rather than simply using the outputs from the final softmax layer of the fine-tuned CNN.
在附录B中,我们讨论了为什么在微调和支持向量机训练中,正负样本的定义不同。我们还讨论了训练检测支持向量机所涉及的权衡,而不是简单地使用微调CNN的最终softmax层的输出
Results on PASCAL VOC 2010-12
PASCAL VOC 2010-12上的结果
Following the PASCAL VOC best practices [15], we validated all design decisions and hyperparameters on the VOC 2007 dataset (Section 3.2). For final results on the VOC 2010-12 datasets, we fine-tuned the CNN on VOC 2012 train and optimized our detection SVMs on VOC 2012 trainval. We submitted test results to the evaluation server only once for each of the two major algorithm variants (with and without bounding-box regression).
遵循PASCAL VOC最佳实践[15],我们验证了VOC 2007数据集上的所有设计决策和超参数(第3.2节)。对于VOC 2010-12数据集的最终结果,我们在VOC 2012训练验证集上对CNN进行了微调,并在VOC 2012训练验证集上优化了SVM检测器。对于两个主要的算法变体,我们只向评估服务器提交一次测试结果(有和没有边界框回归)
Table 1 shows complete results on VOC 2010. We compare our method against four strong baselines, including SegDPM [18], which combines DPM detectors with the output of a semantic segmentation system [4] and uses additional inter-detector context and image-classifier rescoring. The most germane comparison is to the UVA system from Uijlings et al. [39], since our systems use the same region proposal algorithm. To classify regions, their method builds a four-level spatial pyramid and populates it with densely sampled SIFT, Extended OpponentSIFT, and RGBSIFT descriptors, each vector quantized with 4000-word codebooks. Classification is performed with a histogram intersection kernel SVM. Compared to their multi-feature, non-linear kernel SVM approach, we achieve a large improvement in mAP, from 35.1% to 53.7% mAP, while also being much faster (Section 2.2). Our method achieves similar performance (53.3% mAP) on VOC 2011/12 test.
表1显示了VOC 2010的完整结果。我们将我们的方法与四个强基准进行比较,包括SegDPM[18],它将DPM检测器与语义分割系统的输出相结合[4],并使用额外的检测器间上下文和图像分类器重分类。与Uijlings等人[39]的UVA系统进行了最密切的比较,因为我们的系统使用相同的区域建议算法。为了对区域进行分类,他们的方法构建了一个四层空间金字塔,并用密集采样的SIFT、扩展的OpponentSIFT和RGBSIFT描述符对其进行填充,每个向量用4000字码本进行量化。利用直方图交集核SVM进行分类。与它们的多特征、非线性核支持向量机方法相比,我们在mAP上取得了很大的改进,从35.1%提高到53.7%,同时也快得多(第2.2节)。我们的方法在VOC 2011/12测试中达到了类似的性能(53.3%mAP)

Table 1: Detection average precision (%) on VOC 2010 test. R-CNN is most directly comparable to UVA and Regionlets since all methods use selective search region proposals. Bounding-box regression (BB) is described in Section C. At publication time, SegDPM was the top-performer on the PASCAL VOC leaderboard. †DPM and SegDPM use context rescoring not used by the other methods.
表1:VOC 2010试验的检测平均精度百分比。R-CNN最直接地可与UVA和Regionlets进行比较,因为这些方法都使用选择性搜索区域建议。边界框回归(BB)在C节中描述。在出版的时候,SegDPM是PASCAL VOC排行榜上的佼佼者。†DPM和SegDPM使用其他方法未使用的上下文重新排序
Results on ILSVRC2013 detection
在ILSVRC2013检测上的结果
We ran R-CNN on the 200-class ILSVRC2013 detection dataset using the same system hyperparameters that we used for PASCAL VOC. We followed the same protocol of submitting test results to the ILSVRC2013 evaluation server only twice, once with and once without bounding-box regression.
我们在200类ILSVRC2013检测数据集上运行R-CNN,使用与PASCAL VOC相同的系统超参数。我们遵循相同的协议,只向ILSVRC2013评估服务器提交两次测试结果,一次使用边界框回归,一次不使用边界框回归
Figure 3 compares R-CNN to the entries in the ILSVRC 2013 competition and to the post-competition OverFeat result [34]. R-CNN achieves a mAP of 31.4%, which is significantly ahead of the second-best result of 24.3% from OverFeat. To give a sense of the AP distribution over classes, box plots are also presented and a table of perclass APs follows at the end of the paper in Table 8. Most of the competing submissions (OverFeat, NEC-MU, UvA-Euvision, Toronto A, and UIUC-IFP) used convolutional neural networks, indicating that there is significant nuance in how CNNs can be applied to object detection, leading to greatly varying outcomes.
图3将R-CNN与ILSVRC 2013比赛的参赛作品以及赛后的OverFeat成绩进行了比较[34]。R-CNN获得了31.4%的mAP,明显领先于OverFeat的24.3%的第二好成绩。为了了解AP在类上的分布,本文还提供了方框图,并在表8中的文章末尾给出了一个perclass AP表。大多数竞争对手(OverFeat、NEC-MU、UvA-Euvision、Toronto A和UIUC-IFP)都使用了卷积神经网络,这表明CNNs如何应用于目标检测存在显著的细微差别,这会导致结果差异很大
In Section 4, we give an overview of the ILSVRC2013 detection dataset and provide details about choices that we made when running R-CNN on it.
在第4节中,我们概述了ILSVRC2013检测数据集,并提供了有关在其上运行R-CNN时所做选择的详细信息
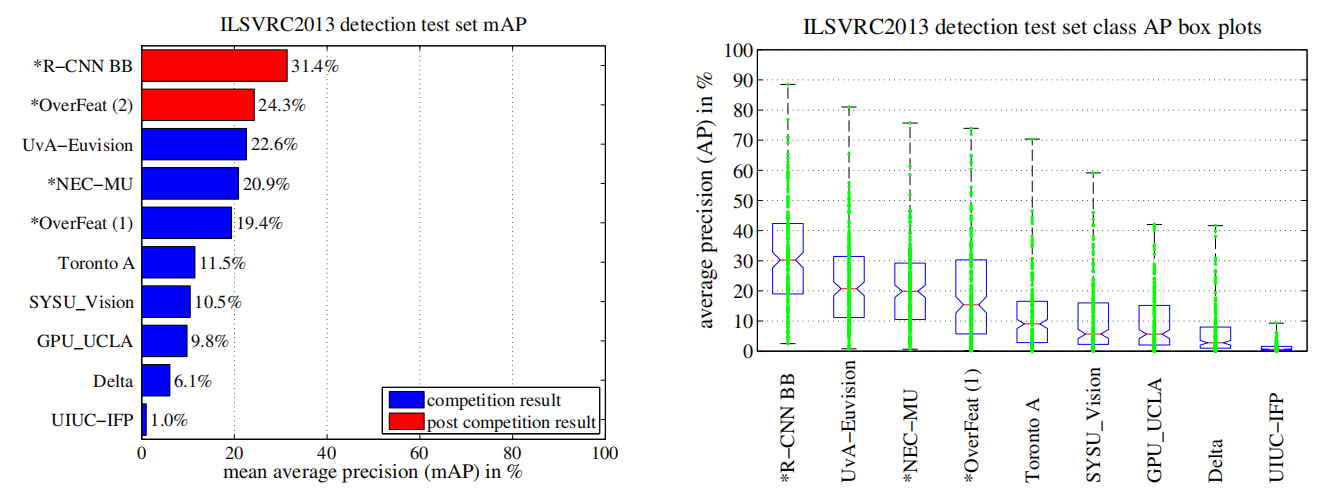
Figure 3: (Left) Mean average precision on the ILSVRC2013 detection test set. Methods preceeded by * use outside training data (images and labels from the ILSVRC classification dataset in all cases). (Right) Box plots for the 200 average precision values per method. A box plot for the post-competition OverFeat result is not shown because per-class APs are not yet available (per-class APs for R-CNN are in Table 8 and also included in the tech report source uploaded to arXiv.org; see R-CNN-ILSVRC2013-APs.txt). The red line marks the median AP, the box bottom and top are the 25th and 75th percentiles. The whiskers extend to the min and max AP of each method. Each AP is plotted as a green dot over the whiskers (best viewed digitally with zoom).
图3:(左)ILSVRC2013检测测试集的平均精度。有*前缀的方法使用外部训练数据(图像和标签来自ILSVRC分类数据集)。(右)每个方法200个平均精度值的方框图。未显示赛后OverFeat成绩的方框图,因为每类AP尚不可用(R-CNN的每类AP见表8,也包括在上传至arXiv.org的技术报告源中;见R-CNN-ILSVRC2013-APs.txt)。红线标记中间AP,方框底部和顶部是25%和75%。晶须延伸至每种方法的最小和最大AP。每个AP都被标绘为胡须上的绿点(最好用数码变焦观看)
Visualization, ablation, and modes of error
可视化、消融和误差模式
Visualizing learned features
可视化学习到的特征
First-layer filters can be visualized directly and are easy to understand [25]. They capture oriented edges and opponent colors. Understanding the subsequent layers is more challenging. Zeiler and Fergus present a visually attractive deconvolutional approach in [42]. We propose a simple (and complementary) non-parametric method that directly shows what the network learned.
第一层滤波器可以直接可视化,并且易于理解[25]。它们捕捉定向的边缘和相对颜色。理解随后的层更具挑战性。Zeiler和Fergus在[42]中提出了一种具有视觉吸引力的反卷积方法。我们提出一个简单的(互补的)非参数方法,直接显示网络所学的内容
The idea is to single out a particular unit (feature) in the network and use it as if it were an object detector in its own right. That is, we compute the unit’s activations on a large set of held-out region proposals (about 10 million), sort the proposals from highest to lowest activation, perform nonmaximum suppression, and then display the top-scoring regions. Our method lets the selected unit “speak for itself” by showing exactly which inputs it fires on. We avoid averaging in order to see different visual modes and gain insight into the invariances computed by the unit.
其思想是在网络中挑出一个特定的单元(特征),并将其作为一个对象检测器来使用。也就是说,我们在一组大的held-out区域建议(大约1000万)上计算单元的激活,将建议从最高到最低的排序,执行非最大抑制,然后显示最高得分区域。我们的方法通过精确显示所选单元触发的输入,让所选单元“为自己说话”。我们避免了平均化以便能够观察不同的视觉模式,并深入了解由单位计算的不变性
We visualize units from layer
, which is the max-pooled output of the network’s fifth and final convolutional layer. The feature map is 6 ×6×256 = 9216-dimensional. Ignoring boundary effects, each unit has a receptive field of 195×195 pixels in the original 227×227 pixel input. A central unit has a nearly global view, while one near the edge has a smaller, clipped support.
我们将第5个池化层中的单元可视化,这是网络第五层也是最后一层卷积的最大池输出。第5个pool的特征图为6×6×256=9216维。忽略边界效应,每个
Each row in Figure 4 displays the top 16 activations for a
unit from a CNN that we fine-tuned on VOC 2007 trainval. Six of the 256 functionally unique units are visualized (Appendix D includes more). These units were selected to show a representative sample of what the network learns. In the second row, we see a unit that fires on dog faces and dot arrays. The unit corresponding to the third row is a red blob detector. There are also detectors for human faces and more abstract patterns such as text and triangular structures with windows. The network appears to learn a representation that combines a small number of class-tuned features together with a distributed representation of shape, texture, color, and material properties. The subsequent fully connected layer fc6 has the ability to model a large set of compositions of these rich features.
图4中的每一行显示了一个CNN的
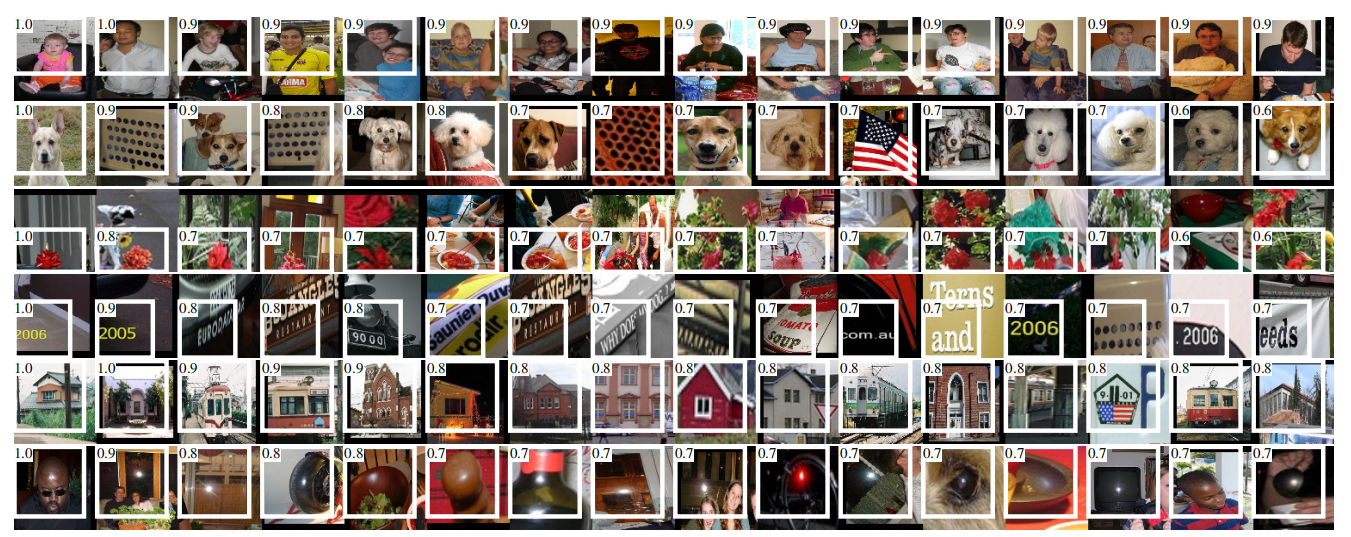
Figure 4: Top regions for six
units. Receptive fields and activation values are drawn in white. Some units are aligned to concepts, such as people (row 1) or text (4). Other units capture texture and material properties, such as dot arrays (2) and specular reflections (6).
图4:6个
Ablation studies
消融研究
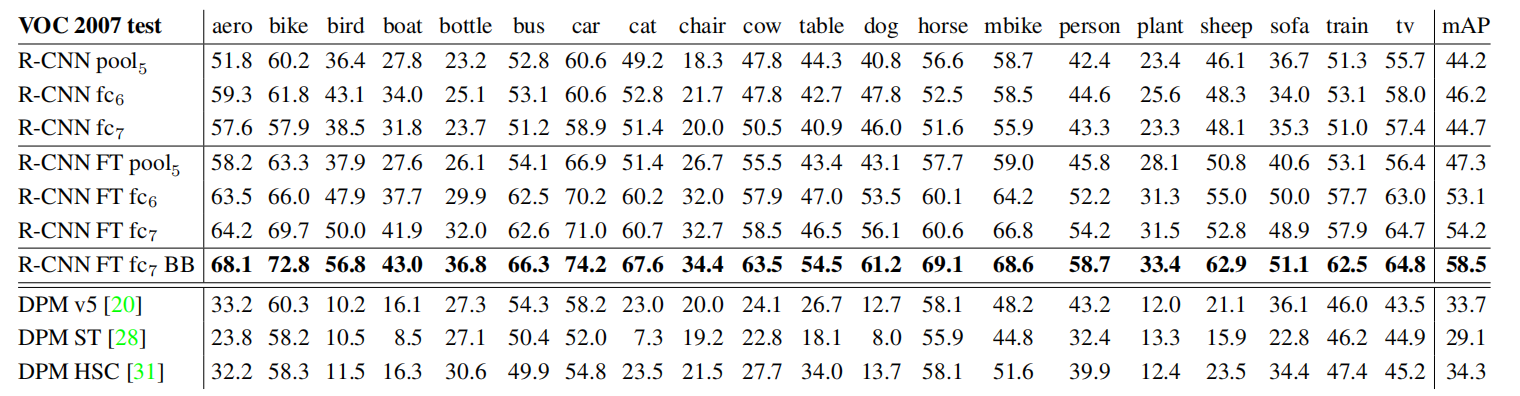
Table 2: Detection average precision (%) on VOC 2007 test. Rows 1-3 show R-CNN performance without fine-tuning. Rows 4-6 show results for the CNN pre-trained on ILSVRC 2012 and then fine-tuned (FT) on VOC 2007 trainval. Row 7 includes a simple bounding-box regression (BB) stage that reduces localization errors (Section C). Rows 8-10 present DPM methods as a strong baseline. The first uses only HOG, while the next two use different feature learning approaches to augment or replace HOG.
表2:在VOC 2007测试集上的检测平均精度。行1-3显示了没有微调的R-CNN性能。行4-6显示了在ILSVRC 2012上预训练,然后在VOC 2007上微调(FT)的结果。第7行包含了一个简单的边界框回归(BB),这样能够减少定位误差(参考附录C)。第8-10行使用DPM方法作为基准线。第一个仅使用HOG特征,另外两个使用不同的特征学习方法来扩充或者替换HOG
Performance layer-by-layer, without fine-tuning. To understand which layers are critical for detection performance, we analyzed results on the VOC 2007 dataset for each of the CNN’s last three layers. Layer
was briefly described in Section 3.1. The final two layers are summarized below.
逐层性能,无需微调。为了了解哪些层对检测性能至关重要,我们分析了CNN最后三层中每个层在VOC 2007数据集中的结果。第3.1节简要介绍了池化层5。最后两层总结如下
Layer
is fully connected to . To compute features, it multiplies a 4096×9216 weight matrix by the feature map (reshaped as a 9216-dimensional vector) and then adds a vector of biases. This intermediate vector is component-wise half-wave rectified (x ← max(0, x)).
We start by looking at results from the CNN without fine-tuning on PASCAL, i.e. all CNN parameters were pre-trained on ILSVRC 2012 only. Analyzing performance layer-by-layer (Table 2 rows 1-3) reveals that features from fc7 generalize worse than features from fc6. This means that 29%, or about 16.8 million, of the CNN’s parameters can be removed without degrading mAP. More surprising is that removing both fc7 and fc6 produces quite good results even though pool5 features are computed using only 6% of the CNN’s parameters. Much of the CNN’s representational power comes from its convolutional layers, rather than from the much larger densely connected layers. This finding suggests potential utility in computing a dense feature map, in the sense of HOG, of an arbitrary-sized image by using only the convolutional layers of the CNN. This representation would enable experimentation with sliding-window detectors, including DPM, on top of pool5 features.
现在开始在PASCAL数据集上研究没有微调的CNN的实现结果,比如所有CNN参数仅在ILSVRC 2012上进行过预训练。逐层分析性能(表2 1-3行)发现fc7层的特征泛化效果低于fc6。这意味着在没有降低mAP的情况下减少了29%,大约1680万个CNN参数。更惊讶的是,同时移除fc7和fc6也能够得到很好的结果,即使pool5的特征仅占所有CNN参数的6%。更多的CNN表示能力来自于卷积层而不是更大的全连接层。这一发现表明,仅使用CNN的卷积层,就HOG的意义而言,在计算任意大小图像的稠密特征图方面具有潜在的实用性。这也让我们能够在pool5特征的基础上,对滑动窗口检测器(包括DPM)进行实验
Performance layer-by-layer, with fine-tuning. We now look at results from our CNN after having fine-tuned its parameters on VOC 2007 trainval. The improvement is striking (Table 2 rows 4-6): fine-tuning increases mAP by 8.0 percentage points to 54.2%. The boost from fine-tuning is much larger for fc6 and fc7 than for pool5 , which suggests that the pool5 features learned from ImageNet are general and that most of the improvement is gained from learning domain-specific non-linear classifiers on top of them.
经过微调后的性能优化。在利用VOC 2007训练验证集对CNN进行微调后,我们现在来看看结果。改进是惊人的(表2第4-6行):微调将mAP提高了8.0个百分点,达到54.2%。微调对fc6和fc7的提升要比pool5大得多,这表明从ImageNet学习到的pool5特性是通用的,而且大部分改进都是通过在它们上面学习领域特定的非线性分类器获得的
The first DPM feature learning method, DPM ST [28], augments HOG features with histograms of "sketch token" probabilities. Intuitively, a sketch token is a tight distribution of contours passing through the center of an image patch. Sketch token probabilities are computed at each pixel by a random forest that was trained to classify 35×35 pixel patches into one of 150 sketch tokens or background.
第一种DPM特征学习方法DPM ST[28]使用“草图标记”概率直方图来增强HOG特征。直观地说,草图标记是通过图像块中心的轮廓的紧密分布。草图标记概率由一个随机森林在每个像素处计算,该森林被训练为将35×35个像素块分类为150个草图标记或背景中的一个
The second method, DPM HSC [31], replaces HOG with histograms of sparse codes (HSC). To compute an HSC, sparse code activations are solved for at each pixel using a learned dictionary of 100 7 × 7 pixel (grayscale) atoms. The resulting activations are rectified in three ways (full and both half-waves), spatially pooled, unit
normalized, and then power transformed ( ).
第二种方法DPM-HSC[31]用稀疏码直方图(HSC)代替HOG。为了计算HSC,使用100个7×7像素(灰度)原子的学习字典来求解每个像素处的稀疏代码激活。由此产生的激活以三种方式(全波和半波)校正,空间合并,单位
All R-CNN variants strongly outperform the three DPM baselines (Table 2 rows 8-10), including the two that use feature learning. Compared to the latest version of DPM, which uses only HOG features, our mAP is more than 20 percentage points higher: 54.2% vs. 33.7%—a 61% relative improvement. The combination of HOG and sketch tokens yields 2.5 mAP points over HOG alone, while HSC improves over HOG by 4 mAP points (when compared internally to their private DPM baselines—both use nonpublic implementations of DPM that underperform the open source version [20]). These methods achieve mAPs of 29.1% and 34.3%, respectively.
所有R-CNN变体都强于三个DPM基线(表2第8-10行),包括使用功能学习的两个基线。与只使用HOG特性的DPM的最新版本相比,我们的mAP高出了20个百分点:54.2%对33.7%,相对提高了61%。HOG和sketch令牌的组合仅比HOG提高了2.5个mAP,而HSC比HOG提高了4个mAP(与它们的私有DPM基线相比,它们都使用了性能低于开源版本[20]的DPM的非公开实现)。这些方法分别得到29.1%和34.3%的图mAP
Network architectures
网络架构
Most results in this paper use the network architecture from Krizhevsky et al. [25]. However, we have found that the choice of architecture has a large effect on R-CNN detection performance. In Table 3 we show results on VOC 2007 test using the 16-layer deep network recently proposed by Simonyan and Zisserman [43]. This network was one of the top performers in the recent ILSVRC 2014 classification challenge. The network has a homogeneous structure consisting of 13 layers of 3 × 3 convolution kernels, with five max pooling layers interspersed, and topped with three fully-connected layers. We refer to this network as “O-Net” for OxfordNet and the baseline as "T-Net" for TorontoNet.
本文中的大多数结果使用了Krizhevsky等人[25]的网络结构。然而,我们发现结构的选择对R-CNN的检测性能有很大的影响。在表3中,我们展示了使用Simonyan和Zisserman最近提出的16层深度网络进行的VOC 2007测试的结果[43]。该网络是最近ILSVRC 2014分类挑战赛中表现最好的网络之一。该网络结构由13层3×3卷积核组成,中间穿插5个最大池化层,顶部为3个完全连通层。我们把这个网络称为OxfordNet的“O-Net”,把TorontoNet的基线称为“T-Net”

Table 3: Detection average precision (%) on VOC 2007 test for two different CNN architectures. The first two rows are results from Table 2 using Krizhevsky et al.’s architecture (T-Net). Rows three and four use the recently proposed 16-layer architecture from Simonyan and Zisserman (O-Net) [43].
表3:使用两种不同的CNN架构在VOC 2007上的检测平均精度(%)。前两行是表2使用Krizhevsky等人的架构(T-Net)得出的结果。第3行和第4行使用了Simonyan和Zisserman(O-Net)最近提出的16层体系结构[43]
To use O-Net in R-CNN, we downloaded the publicly available pre-trained network weights for the VGG ILSVRC 16 layers model from the Caffe Model Zoo. We then fine-tuned the network using the same protocol as we used for T-Net. The only difference was to use smaller minibatches (24 examples) as required in order to fit within GPU memory. The results in Table 3 show that R-CNN with O-Net substantially outperforms R-CNN with T-Net, increasing mAP from 58.5% to 66.0%. However there is a considerable drawback in terms of compute time, with the forward pass of O-Net taking roughly 7 times longer than T-Net.
为了在R-CNN中使用O-Net,我们从Caffe model Zoo下载了VGG ILSVRC 16层模型的公共预训练网络权重。然后,我们使用与T-Net相同的协议对网络进行微调。唯一的区别是根据需要使用更小的小批量(24个示例),以便适合GPU内存。表3的结果表明,使用O-Net的R-CNN明显优于使用T-Net的R-CNN,mAP从58.5%增加到66.0%。然而,在计算时间方面有一个相当大的缺点,即O-Net的前向通过时间大约是T-Net的7倍
Detection error analysis
检测误差分析
We applied the excellent detection analysis tool from Hoiem et al. [23] in order to reveal our method’s error modes, understand how fine-tuning changes them, and to see how our error types compare with DPM. A full summary of the analysis tool is beyond the scope of this paper and we encourage readers to consult [23] to understand some finer details (such as "normalized AP"). Since the analysis is best absorbed in the context of the associated plots, we present the discussion within the captions of Figure 5 and Figure 6.
我们使用了Hoiem等人[23]优秀的检测分析工具。为了揭示我们方法的错误模式,理解微调如何更改它们,并查看我们的错误类型与DPM的比较。对分析工具的全面总结超出了本文的范围,我们鼓励读者参考[23]以了解一些更详细的信息(例如“规范化AP”)。由于分析最好是在相关图的上下文中进行,因此我们在图5和图6的标题中进行讨论
Qualitative results
定性结果
Qualitative detection results on ILSVRC2013 are presented in Figure 8 and Figure 9 at the end of the paper. Each image was sampled randomly from the val2 set and all detections from all detectors with a precision greater than 0.5 are shown. Note that these are not curated and give a realistic impression of the detectors in action. More qualitative results are presented in Figure 10 and Figure 11, but these have been curated. We selected each image because it contained interesting, surprising, or amusing results. Here, also, all detections at precision greater than 0.5 are shown.
ILSVRC2013的定性检测结果如文末图8和图9所示。每个图像从val2集合中随机采样,显示所有检测器精度大于0.5的所有检测结果。请注意,这些没有经过挑选。更多的定性结果如图10和图11所示,但这些结果已得到处理。我们选择每个图像是因为它包含有趣、令人惊讶或有趣的结果。这里还显示了精度大于0.5的所有检测
The ILSVRC2013 detection dataset
ILSVRC2013检测数据集
In Section 2 we presented results on the ILSVRC2013 detection dataset. This dataset is less homogeneous than PASCAL VOC, requiring choices about how to use it. Since these decisions are non-trivial, we cover them in this section.
在第2节中,我们介绍了ILSVRC2013检测数据集的结果。这个数据集不如PASCAL VOC同质,需要选择如何使用它。由于这些决定是有意义的,我们将在本节介绍它们
Dataset overview
数据集概述
The ILSVRC2013 detection dataset is split into three sets: train (395,918), val (20,121), and test (40,152), where the number of images in each set is in parentheses. The val and test splits are drawn from the same image distribution. These images are scene-like and similar in complexity (number of objects, amount of clutter, pose variability, etc.) to PASCAL VOC images. The val and test splits are exhaustively annotated, meaning that in each image all instances from all 200 classes are labeled with bounding boxes. The train set, in contrast, is drawn from the ILSVRC2013 classification image distribution. These images have more variable complexity with a skew towards images of a single centered object. Unlike val and test, the train images (due to their large number) are not exhaustively annotated. In any given train image, instances from the 200 classes may or may not be labeled. In addition to these image sets, each class has an extra set of negative images. Negative images are manually checked to validate that they do not contain any instances of their associated class. The negative image sets were not used in this work. More information on how ILSVRC was collected and annotated can be found in [11, 36].
ILSVRC2013检测数据集分为三组:train(395918)、val(20121)和test(40152),每组中的图像数在括号中。val和test分割是从相同的图像分布中提取的。这些图像在PASCAL VOC图像中是复杂的(对象数量、杂波、姿态变化等)。val和test split是完全注释的,这意味着在每个图像中,所有200个类的所有实例都用边界框标记。相反,训练集是从ILSVRC2013分类图像分布中提取的。 这些图像具有更多的可变复杂度,歪斜朝向单个中心对象的图像。与val和test不同,训练图像(由于其数量庞大)没有完全注释。在任何给定的训练图像中,来自200个类的实例可以被标记,也可以不被标记。除了这些图像集之外,每个类还有一组额外的负样本图像。手动检查负样本图像,以验证它们不包含其关联类的任何实例。这项工作没有使用负样本图像集。关于ILSVRC是如何收集和注释的更多信息可以在[11,36]中找到
The nature of these splits presents a number of choices for training R-CNN. The train images cannot be used for hard negative mining, because annotations are not exhaustive. Where should negative examples come from? Also, the train images have different statistics than val and test. Should the train images be used at all, and if so, to what extent? While we have not thoroughly evaluated a large number of choices, we present what seemed like the most obvious path based on previous experience.
这些分离的性质为训练R-CNN提供了许多选择。训练图像不能用于hard negative mining,因为标注不完全。负样本应该从哪里来另外,训练图像与val和test有不同的统计特性。训练图像应该被使用吗?如果是的话,使用到什么程度?虽然我们没有对大量的选择进行彻底的评估,但根据以往的经验,我们提出了似乎是最明显的途径
Our general strategy is to rely heavily on the val set and use some of the train images as an auxiliary source of positive examples. To use val for both training and validation, we split it into roughly equally sized "val1" and "val2" sets. Since some classes have very few examples in val (the smallest has only 31 and half have fewer than 110), it is important to produce an approximately class-balanced partition. To do this, a large number of candidate splits were generated and the one with the smallest maximum relative class imbalance was selected.2 Each candidate split was generated by clustering val images using their class counts as features, followed by a randomized local search that may improve the split balance. The particular split used here has a maximum relative imbalance of about 11% and a median relative imbalance of 4%. The val1/val2 split and code used to produce them will be publicly available to allow other researchers to compare their methods on the val splits used in this report.
我们的总体策略是严重依赖于验证集,并使用一些训练图像作为正样本的辅助来源。为了使用val进行训练和验证,我们将其分成大小大致相同的“val1”和“val2”集。由于一些类在var中的例子很少(最小的只有31,有一半类小于110),因此产生一个近似的类平衡分区是很重要的。为此,生成了大量的候选分割,并选择了最小的相对最大类失衡的2个候选分割,通过使用类计数作为特征来聚类val图像生成每个候选分割,然后通过随机化局部搜索来改善分割平衡。这里使用的特定分割具有最大相对不平衡约11%和中值相对不平衡4%。val1/val2拆分和用于生成它们的代码将公开,以便其他研究人员可以比较他们在本报告中使用的val拆分方法
Region Proposals
区域建议
We followed the same region proposal approach that was used for detection on PASCAL. Selective search [39] was run in “fast mode” on each image in val1, val2, and test (but not on images in train). One minor modification was required to deal with the fact that selective search is not scale invariant and so the number of regions produced depends on the image resolution. ILSVRC image sizes range from very small to a few that are several mega-pixels, and so we resized each image to a fixed width (500 pixels) before running selective search. On val, selective search resulted in an average of 2403 region proposals per image with a 91.6% recall of all ground-truth bounding boxes (at 0.5 IoU threshold). This recall is notably lower than in PASCAL, where it is approximately 98%, indicating significant room for improvement in the region proposal stage.
我们遵循了用于PASCAL检测的相同区域建议方法。选择性搜索[39]在val1、val2和test中的每个图像上以“快速模式”运行(但不在训练中的图像上)。为了解决选择性搜索不具有尺度不变性的问题,需要做一个小的修改,因此产生的区域数取决于图像的分辨率。ILSVRC图像的大小从很小到几兆像素不等,因此在运行选择性搜索之前,我们将每个图像的大小调整为固定宽度(500像素)。 在val上,选择性搜索平均每幅图像产生2403个区域建议,91.6%的ground-truth边界框召回率(IoU阈值为0.5)。这一召回率明显低于PASCAL,约为98%,表明在区域建议阶段有很大的改进空间
... ... ... ...
Conclusion
In recent years, object detection performance had stagnated. The best performing systems were complex ensembles combining multiple low-level image features with high-level context from object detectors and scene classifiers. This paper presents a simple and scalable object detection algorithm that gives a 30% relative improvement over the best previous results on PASCAL VOC 2012.
近年来,目标检测性能停滞不前。性能最好的系统是将多个低级图像特征与来自目标检测器和场景分类器的高级上下文结合起来的复杂集合。本文提出了一种简单且可扩展的目标检测算法,与PASCAL VOC 2012上的最佳结果相比,相对提高了30%
We achieved this performance through two insights. The first is to apply high-capacity convolutional neural networks to bottom-up region proposals in order to localize and segment objects. The second is a paradigm for training large CNNs when labeled training data is scarce. We show that it is highly effective to pre-train the network - with supervision - for a auxiliary task with abundant data (image classification) and then to fine-tune the network for the target task where data is scarce (detection). We conjecture that the “supervised pre-training/domain-specific fine tuning” paradigm will be highly effective for a variety of data-scarce vision problems.
我们通过两个观点实现了这一性能。首先,将大容量卷积神经网络应用于自下而上的区域建议,以便对对象进行定位和分割。第二种是在标记训练数据稀少的情况下训练大型CNN的范例。我们表明在数据稀缺的情况下,通过预训练网络,然后微调网络的目标任务是很有效的。我们推测“有监督的预训练/领域特定精细调整”范式对于各种数据稀缺的视觉问题将是非常有效的
We conclude by noting that it is significant that we achieved these results by using a combination of classical tools from computer vision and deep learning (bottom-up region proposals and convolutional neural networks). Rather than opposing lines of scientific inquiry, the two are natural and inevitable partners.
最后,我们注意到,通过使用计算机视觉和深度学习(自下而上的区域建议和卷积神经网络)的经典工具的组合来实现这些结果是非常重要的。这两者不是科学探究的界限,而是自然和不可避免的合作伙伴
Appendix
附录
Object proposal transformations
目标建议转换

Figure 7: Different object proposal transformations. (A) the original object proposal at its actual scale relative to the transformed CNN inputs; (B) tightest square with context; (C) tightest square without context; (D) warp. Within each column and example proposal, the top row corresponds to p = 0 pixels of context padding while the bottom row has p = 16 pixels of context padding.
图7:不同的目标建议转换。(A)相对于转换后的CNN输入,其实际规模的原始目标建议;(B)结合背景的最紧正方形;(C)不结合背景的最紧正方形;(D)扭曲。在每列和示例建议中,第一行对应于p=0像素的上下文填充,而第二行对应于p=16像素的上下文填充
The convolutional neural network used in this work requires a fixed-size input of 227 × 227 pixels. For detection, we consider object proposals that are arbitrary image rectangles. We evaluated two approaches for transforming object proposals into valid CNN inputs.
本文所使用的卷积神经网络需要227×227像素的固定大小输入。对于检测,我们考虑的对象建议是任意图像矩形。我们评估了将目标建议转换为有效CNN输入的两种方法
The first method ("tightest square with context") encloses each object proposal inside the tightest square and then scales (isotropically) the image contained in that square to the CNN input size. Figure 7 column (B) shows this transformation. A variant on this method ("tightest square without context") excludes the image content that surrounds the original object proposal. Figure 7 column (C) shows this transformation. The second method ("warp") anisotropically scales each object proposal to the CNN input size. Figure 7 column (D) shows the warp transformation.
第一种方法(“带上下文的最紧密的正方形”)将每个对象建议包含在最紧密的正方形中,然后(各向同性地)将该正方形中包含的图像缩放到CNN输入大小。 图7(B)列显示了这种转换。此方法的变体(“没有上下文的最紧正方形”)排除围绕原始对象方案的图像内容。图7(C)列显示了这种转换。第二种方法(“warp”)各向异性地将每个对象方案缩放到CNN输入大小。图7(D)列显示了扭曲变换
For each of these transformations, we also consider including additional image context around the original object proposal. The amount of context padding (p) is defined as a border size around the original object proposal in the transformed input coordinate frame. Figure 7 shows p = 0 pixels in the top row of each example and p = 16 pixels in the bottom row. In all methods, if the source rectangle extends beyond the image, the missing data is replaced with the image mean (which is then subtracted before inputing the image into the CNN). A pilot set of experiments showed that warping with context padding (p = 16 pixels) outperformed the alternatives by a large margin (3-5 mAP points). Obviously more alternatives are possible, including using replication instead of mean padding. Exhaustive evaluation of these alternatives is left as future work.
对于这些转换中的每一个,我们还考虑在原始对象方案周围包含额外的图像上下文。上下文填充量(p)定义为转换后的输入坐标框中原始对象建议周围的边框大小。图7显示了每个示例的顶行中的p=0像素和底行中的p=16像素。在所有方法中,如果源矩形超出图像,则用图像平均值替换丢失的数据(然后在将图像输入CNN之前减去图像平均值)。一组试验表明,使用上下文填充(p=16像素)进行扭曲比使用其他方法(3-5个mAP)的效果好得多。显然还有更多的选择,包括使用复制而不是平均填充。对这些备选方案的详尽评估将留待以后的工作
Positive vs. negative examples and softmax
正样本 vs. 负样本 和softmax
Two design choices warrant further discussion. The first is: Why are positive and negative examples defined differently for fine-tuning the CNN versus training the object detection SVMs? To review the definitions briefly, for fine-tuning we map each object proposal to the ground-truth instance with which it has maximum IoU overlap (if any) and label it as a positive for the matched ground-truth class if the IoU is at least 0.5. All other proposals are labeled "background" (i.e., negative examples for all classes). For training SVMs, in contrast, we take only the ground-truth boxes as positive examples for their respective classes and label proposals with less than 0.3 IoU overlap with all instances of a class as a negative for that class. Proposals that fall into the grey zone (more than 0.3 IoU overlap, but are not ground truth) are ignored.
有两种设计选择值得进一步讨论。第一个问题是:为什么对于微调CNN和训练目标检测支持向量机,正负样本的定义不同?为了简要地回顾这些定义,为了微调,我们将每个目标建议映射到其具有最大IOU重叠(如果有的话)的ground-truth实例,并且如果IoU至少为0.5,才将其标记为匹配的ground-truth类的正样本。所有其他建议都标为“背景”(即所有类别的负样本)。相比之下,对于SVM的培训,我们仅将ground-truth框作为其各自类的正样本,并将IoU重叠小于0.3的建议与类的所有实例标记为该类的负样本。属于灰色地带的提案(IoU重叠超过0.3,但不是ground-truth)被忽略
Our hypothesis is that this difference in how positives and negatives are defined is not fundamentally important and arises from the fact that fine-tuning data is limited. Our current scheme introduces many "jittered" examples (those proposals with overlap between 0.5 and 1, but not ground truth), which expands the number of positive examples by approximately 30x. We conjecture that this large set is needed when fine-tuning the entire network to avoid overfitting. However, we also note that using these jittered examples is likely suboptimal because the network is not being fine-tuned for precise localization.
我们的假设是,正样本和负样本的定义方式上的这种差异并不是根本上重要的,而是因为微调数据是有限的。我们目前的方案引入了许多“抖动”的例子(那些重叠在0.5和1之间的建议,但不是ground truth),它将正面例子的数量扩大了大约30x。我们推测在对整个网络进行微调以避免过度拟合时,需要这个大集合。然而,我们也注意到,使用这些不稳定的例子可能是次优的,因为网络并没有为精确的定位进行微调
This leads to the second issue: Why, after fine-tuning, train SVMs at all? It would be cleaner to simply apply the last layer of the fine-tuned network, which is a 21-way softmax regression classifier, as the object detector. We tried this and found that performance on VOC 2007 dropped from 54.2% to 50.9% mAP. This performance drop likely arises from a combination of several factors including that the definition of positive examples used in fine-tuning does not emphasize precise localization and the softmax classifier was trained on randomly sampled negative examples rather than on the subset of “hard negatives” used for SVM training.
这就引出了第二个问题:在微调之后,为什么还要训练SVM?简单地将微调网络的最后一层(21类Softmax回归分类器)用作目标检测器会更干净。我们尝试了一下,发现VOC 2007的性能从54.2%下降到了50.9%。这种性能下降可能是多种因素共同作用的结果,包括微调中使用的正样本的定义不强调精确定位,并且softmax分类器是在随机抽样的负样本上训练的,而不是在用于支持向量机训练的“hard positives”子集上训练的
This result shows that it’s possible to obtain close to the same level of performance without training SVMs after fine-tuning. We conjecture that with some additional tweaks to fine-tuning the remaining performance gap may be closed. If true, this would simplify and speed up R-CNN training with no loss in detection performance.
结果表明,经过微调后,无需对支持向量机进行训练,就可以获得接近相同水平的性能。我们推测,通过一些额外的微调,可以缩小剩余的性能差距。如果是真的,这将简化和加速R-CNN训练,而不会损失检测性能
Bounding-box regression
边界框回归
We use a simple bounding-box regression stage to improve localization performance. After scoring each selective search proposal with a class-specific detection SVM, we predict a new bounding box for the detection using a class-specific bounding-box regressor. This is similar in spirit to the bounding-box regression used in deformable part models [17]. The primary difference between the two approaches is that here we regress from features computed by the CNN, rather than from geometric features computed on the inferred DPM part locations.
我们使用一个简单的边界框回归阶段来提高定位性能。在用类特定的检测支持向量机对每个选择性搜索方案进行评分后,我们使用类特定的边界框回归器预测新的检测边界框。这在定义上类似于可变形零件模型中使用的边界框回归[17]。这两种方法的主要区别在于,这里我们从CNN计算的特征回归,而不是从根据推断的DPM零件位置计算的几何特征回归
The input to our training algorithm is a set of N training pairs
, where specifies the pixel coordinates of the center of proposal ’s bounding box together with ’s width and height in pixels. Hence forth, we drop the superscript i unless it is needed. Each ground-truth bounding box G is specified in the same way: . Our goal is to learn a transformation that maps a proposed box P to a ground-truth box G.
我们训练算法的输入是N个训练对
We parameterize the transformation in terms of four functions
. The first two specify a scale-invariant translation of the center of P’s bounding box, while the second two specify log-space translations of the width and height of P’s bounding box. After learning these functions, we can transform an input proposal P into a predicted ground-truth box by applying the transformation
我们将转换参数化为四个函数
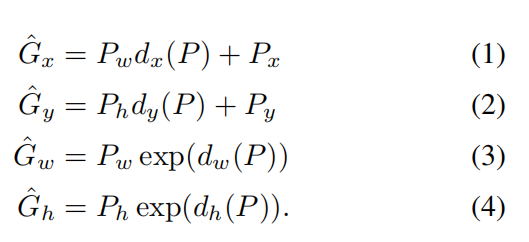
Each function
(where $$ is one of x, y, h, w) is modeled as a linear function of the pool5 features of proposal P, denoted by . (The dependence of on the image data is implicitly assumed.) Thus we have , where is a vector of learnable model parameters. We learn by optimizing the regularized least squares objective (ridge regression):
每个函数
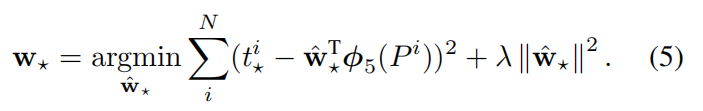
The regression targets
训练对(p,G)的回归目标
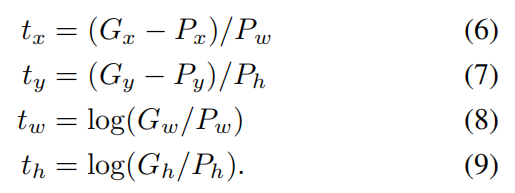
As a standard regularized least squares problem, this can be solved efficiently in closed form.
作为一个标准的正则化最小二乘问题,它可以有效地用封闭形式求解
We found two subtle issues while implementing bounding-box regression. The first is that regularization is important: we set λ = 1000 based on a validation set. The second issue is that care must be taken when selecting which training pairs (P, G) to use. Intuitively, if P is far from all ground-truth boxes, then the task of transforming P to a ground-truth box G does not make sense. Using examples like P would lead to a hopeless learning problem. Therefore, we only learn from a proposal P if it is nearby at least one ground-truth box. We implement "nearness" by assigning P to the ground-truth box G with which it has maximum IoU overlap (in case it overlaps more than one) if and only if the overlap is greater than a threshold (which we set to 0.6 using a validation set). All unassigned proposals are discarded. We do this once for each object class in order to learn a set of class-specific bounding-box regressors.
在实现边界框回归时,我们发现了两个微妙的问题。首先,正则化很重要:我们基于验证集设置λ=1000。第二个问题是,在选择要使用的训练对(P,G)时必须小心。直观地说,如果P远离所有的真样本框,那么将P转换为真真值框G的任务就没有意义。使用像P这样的例子会导致一个无望的学习问题。因此,我们只能从一个方案P中学习,如果它至少在一个真样本框附近。我们实现“接近”通过分配P到真样本框G,当它和仅当重叠大于阈值(使用验证集设置为0.6)时,它具有最大的IoU重叠(某些情况下它重叠不止一个)。所有未分配的建议都将被丢弃。我们对每个对象类执行一次此操作,以便学习一组特定于类的边界框回归器
Gitalk 加载中 ...