[LR Scheduler]余弦退火
余弦退火(Cosine Annealing)方法来自于论文SGDR: STOCHASTIC GRADIENT DESCENT WITH WARM RESTARTS
摘要
Restart techniques are common in gradient-free optimization to deal with multimodal functions. Partial warm restarts are also gaining popularity in gradientbased optimization to improve the rate of convergence in accelerated gradient schemes to deal with ill-conditioned functions. In this paper, we propose a simple warm restart technique for stochastic gradient descent to improve its anytime performance when training deep neural networks. We empirically study its performance on the CIFAR-10 and CIFAR-100 datasets, where we demonstrate new state-of-the-art results at 3.14% and 16.21%, respectively. We also demonstrate its advantages on a dataset of EEG recordings and on a downsampled version of the ImageNet dataset. Our source code is available at https://github.com/loshchil/SGDR
重启技术在处理多峰函数的无梯度优化中很常见。局部热重启在基于梯度的优化中也越来越受欢迎,以提高加速梯度方案处理病态函数的收敛速度。在本文中,我们提出了一种简单的随机梯度下降热重启技术,以提高其在训练深度神经网络时的实时性。我们对其在CIFAR-10和CIFAR-100数据集上的性能进行了训练研究,分别得到了3.14%和16.21%的最好结果。我们还展示了它在EEG记录数据集和下采样版本的ImageNet数据集上的优势。代码实现地址:https://github.com/loshchil/SGDR
PyTorch实现
PyTorch提供了两个版本的余弦退火:
CosineAnnealingLR
定义
class torch.optim.lr_scheduler.CosineAnnealingLR(optimizer, T_max, eta_min=0, last_epoch=-1)
optimizer:优化器T_max:最大迭代次数eta_min:最小学习率。默认为0last_epoch:最新一轮。默认为-1
其实现公式如下:
\[ \eta _{t} = \eta_{min} + \frac {1}{2} (\eta_{max} - \eta_{min}) (1 + \cos (\frac {T_{cur}}{T_{max}}\pi)) \]
- \(\eta_{t}\):学习率
- \(\eta_{max}\):最大学习率
- \(\eta_{min}\):最小学习率。可设置
- \(T_{cur}\):当前迭代次数
- \(T_{max}\):最大迭代次数
实现
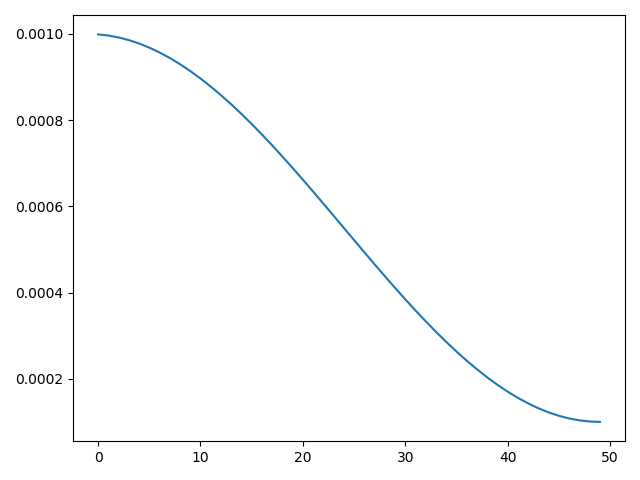
该函数仅实现了一个周期的余弦退火,可用于平缓的下降学习率
1 | import torch.optim as optim |
CosineAnnealingWarmRestarts
定义
class torch.optim.lr_scheduler.CosineAnnealingWarmRestarts(optimizer, T_0, T_mult=1, eta_min=0, last_epoch=-1)
optimizer:优化器T_0:重启后的迭代次数T_mult:每次重启后增加迭代次数的乘法因子。默认为1eta_min:最小学习率。默认为0last_epoch:最新一轮。默认为-1
其实现公式如下:
\[ \eta _{t} = \eta_{min} + \frac {1}{2} (\eta_{max} - \eta_{min}) (1 + \cos (\frac {T_{cur}}{T_{i}}\pi)) \]
- \(\eta_{t}\):学习率
- \(\eta_{max}\):最大学习率
- \(\eta_{min}\):最小学习率。可设置
- \(T_{cur}\):重启后的迭代次数
- \(T_{i}\):第\(i\)论的迭代次数
当\(T_{cur}=T_{i}\)时,设置\(\eta_{t}=\eta_{min}\);每次重启后当\(T_{cur}=0\)时,设置\(\eta_{t}=\eta_{max}\)
实现
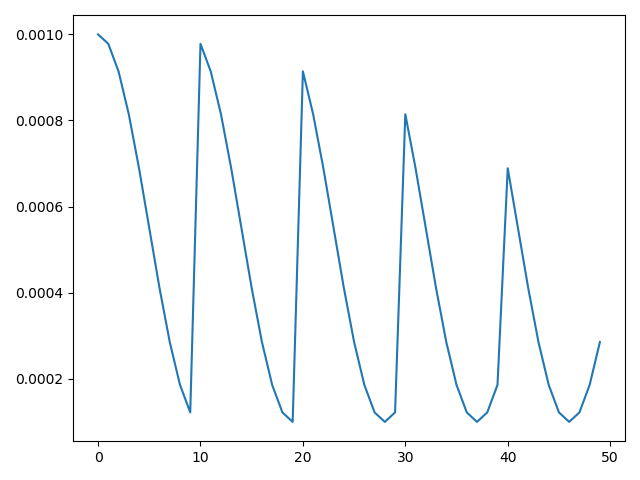
CosineAnnealingWarmRestarts实现了多周期的余弦退火
1 | import torch.optim as optim |
余弦退火+模型集成
余弦退火方法的目的在于逃离当前局部最优点,寻找新的局部最优点。在每个周期计算完成后,保存不同局部最优点的模型参数。参考使用余弦退火逃离局部最优点——快照集成(Snapshot Ensembles)在Keras上的应用,因为不同局部最优点的模型存到较大的多样性,所以集合之后效果会更好