如何找到最优权重衰减值

发表于 2020-05-03 更新于 2021-04-14 分类于深度学习/deeplearning 阅读次数：

本文字数： 35k 阅读时长 ≈ 1:04

论文A DISCIPLINED APPROACH TO NEURAL NETWORK HYPER-PARAMETERS: PART 1 – LEARNING RATE, BATCH SIZE, MOMENTUM, AND WEIGHT DECAY给出了关于学习率、批量大小、动量和权重衰减的训练方法。下面学习如何找到最优权重衰减值

摘要

Although deep learning has produced dazzling successes for applications of image, speech, and video processing in the past few years, most trainings are with suboptimal hyper-parameters, requiring unnecessarily long training times. Setting the hyper-parameters remains a black art that requires years of experience to acquire. This report proposes several efficient ways to set the hyper-parameters that significantly reduce training time and improves performance. Specifically, this report shows how to examine the training validation/test loss function for subtle clues of underfitting and overfitting and suggests guidelines for moving toward the optimal balance point. Then it discusses how to increase/decrease the learning rate/momentum to speed up training. Our experiments show that it is crucial to balance every manner of regularization for each dataset and architecture. Weight decay is used as a sample regularizer to show how its optimal value is tightly coupled with the learning rates and momentum. Files to help replicate the results reported here are available at https://github.com/lnsmith54/hyperParam1.

尽管在过去几年中，深度学习在图像、语音和视频处理的应用方面取得了令人眼花缭乱的成功，但大多数训练都采用了次优的超参数，造成了不必要的长时间训练。设置超参数仍然是一种需要多年经验才能获得的黑色艺术。本报告提出了几个设置超参数的有效方法，可显著减少训练时间并提高性能。具体而言，本报告展示了如何检查训练验证/测试损失函数，以寻找拟合不足和拟合过度的细微线索，并提出了走向最佳平衡点的指导方针。然后讨论如何增加/减少学习速度/动量以加速训练。我们的实验表明，平衡每个数据集和架构的每种正则化方式是至关重要的。权重衰减被用作样本正则化器，以显示其最优值如何与学习率和动量紧密耦合。相关实验参数保存在https://github.com/lnsmith54/hyperParam1

4.4 WEIGHT DECAY

Weight decay is one form of regularization and it plays an important role in training so its value needs to be set properly. The important point made above applies; that is, practitioners must balance the various forms of regularization to obtain good performance. The interested reader can see Kukacka et al. (2017) for a review of regularization methods.

权重衰减是正则化的一种形式，它在训练中起着重要的作用，因此需要适当地设置其值。上述要点适用；也就是说，实现者必须平衡各种形式的正则化以获得良好的性能。感兴趣的读者可以查看Kukacka等人(2017)对于正则化方法的评估

Our experiments show that weight decay is not like learning rates or momentum and the best value should remain constant through the training (i.e., cyclical weight decay is not useful). This appears to be generally so for regularization but was not tested for all regularization methods (a more complete study of regularization is planned for Part 2 of this report). Since the network’s performance is dependent on a proper weight decay value, a grid search is worthwhile and differences are visible early in the training. That is, the validation loss early in the training is sufficient for determining a good value. As shown below, a reasonable procedure is to make combined CLR and CM runs at a few values of the weight decay in order to simultaneously determine the best learning rates, momentum and weight decay.

我们的实验表明，权重衰减不像学习率或动量，最佳值应该在整个训练过程中保持不变(即周期性权重衰减没有用)。对于正则化来说，这似乎是普遍的，但是并没有对所有正则化方法进行测试(计划在本报告的第二部分对正则化进行更全面的研究)。由于网络的性能取决于适当的权重衰减值，因此网格搜索是值得的，并且在训练的早期就可以看到差异。也就是说，训练早期的验证损失足以确定一个好的值。如下图所示，一个合理的步骤是组合CLR（循环学习率）和CM（循环动量），和权重衰减的几个候选一起运行，以便同时确定最佳学习速率、动量和权重衰减

If you have no idea of a reasonable value for weight decay, test \(10^{−3}, 10^{−4} , 10^{−5}\) , and 0. Smaller datasets and architectures seem to require larger values for weight decay while larger datasets and deeper architectures seem to require smaller values. Our hypothesis is that complex data provides its own regularization and other regularization should be reduced.

默认测试4个候选值：\(10^{−3}, 10^{−4} , 10^{−5}\) 和0。 较小的数据集和架构似乎需要较大的权重衰减值，而较大的数据集和较深的架构似乎需要较小的值。我们的假设是，复杂数据提供了自己的正则化，其他正则化应该减少

On the other hand, if your experience indicates that a weight decay value of \(10^{−4}\) should be about right, these initial runs might be at \(3×10^{−5} , 10^{−4} , 3×10^{−4}\) . The reasoning behind choosing \(3\) rather than \(5\) is that a magnitude is needed for weight decay so this report suggests bisection of the exponent rather than bisecting the value (i.e., between \(10^{−4}\) and \(10^{−3}\) one bisects as \(10^{−3.5} = 3.16 × 10^{−4})\). Afterwards, make a follow up run that bisects the exponent of the best two of these or if none seem best, extrapolate towards an improved value.

另一方面，如果经验表明\(10^{−4}\)的权重衰减值应该是正确的，那么下一步的初始测试可能在\(3×10^{−4}、10^{−4}、3×10^{−5}\)中进行。选择\(3\)而不是\(5\)的原因是权重衰减需要一个量级，因此本报告建议将指数一分为二，而不是将数值一分为二（即在\(10^{−4}\)和\(10^{−3}\)之间，将指数一分为二得到\(10^{−3.5} = 3.16 × 10^{−4})\)）。然后进行一次后续运行，将其中最好的两个指数一分为二，或者如果没有最好的，则推断出一个改进的值

Remark 6. Since the amount of regularization must be balanced for each dataset and architecture, the value of weight decay is a key knob to turn for tuning regularization against the regularization from an increasing learning rate. While other forms of regularization are generally fixed (i.e., dropout ratio, stochastic depth), one can easily change the weight decay value when experimenting with maximum learning rate and stepsize values.

备注6。由于正则化的大小必须针对每个数据集和架构进行平衡，权重衰减的值是一个关键，用于根据不断增加的学习率来调整正则化。虽然其他形式的正则化通常是固定的(比如随机失活、随机深度)，但是当实验最大学习率和步长值时，可以很容易地改变权重衰减值

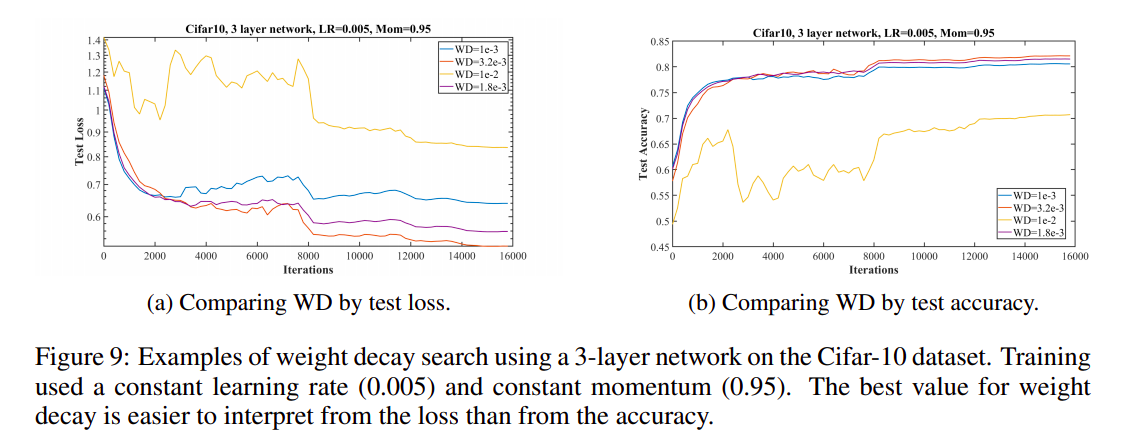
Figure 9a shows the validation loss of a grid search for a 3-layer network on Cifar-10 data, after assuming a learning rate of 0.005 and momentum of 0.95. Here it would be reasonable to run values of \(1×10^{−2} , 3.2×10^{−3} , 10^{−3}\) , which are shown in the Figure. Clearly the yellow curve implies that \(1 × 10^{−2}\) is too large and the blue curve implies that \(10^{−3}\) is too small (notice the overfitting). After running these three, a value of \(3.2 × 10^{−3}\) seems right but one can also make a run with a weight decay value of \(10^{−2.75} = 1.8 × 10^{−3}\) , which is the purple curve. This confirms that \(3.2 × 10^{−3}\) is a good choice. Figure 9b shows the accuracy results from trainings at all four of these values and it is clear that the validation loss is predictive of the best final accuracy.

图9a显示在假设学习率为0.005，动量为0.95，在Cifar-10数据上对3层网络进行网格搜索的有效性损失。在这里，运行如图所示的\(1×10^{−2}、3.2×10^{−3}、10^{−3}\)的值是合理的。显然，黄色曲线意味着\(1× 10^{−2}\)太大，蓝色曲线意味着\(10^{−3}\)太小（注意过拟合）。运行这三个之后，\(3.2× 10^{−3}\)似乎是正确的，但是也可以运行\(10^{−2.75} = 1.8 × 10^{−3}\)的权重衰减值，这是紫色曲线。这证实了\(3.2× 10^{−3}\)是一个不错的选择。图9b显示了所有四个值的训练精度结果，很明显通过损失值能够预测相应的精度

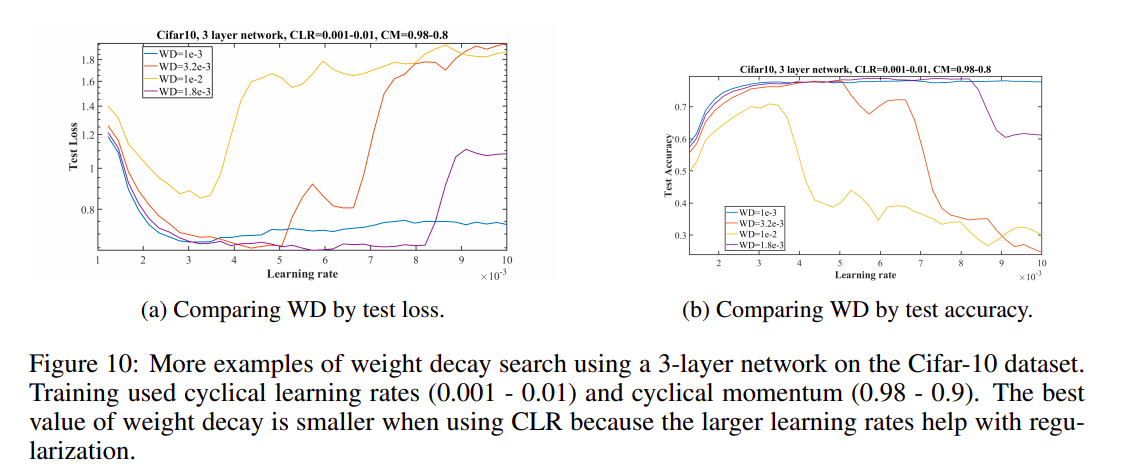
A reasonable question is can the value for the weight decay, learning rate and momentum all be determined simultaneously? Figure 10a shows the runs of a learning rate range test (LR = 0.001 - 0.01) along with a decreasing momentum (= 0.98 - 0.8) at weight decay values of \(10^{−2} , 3.2 × 10^{−3} , 10^{−3}\) . As before, a value of \(3.2 × 10^{−3}\) seems best. However, a test of weight decay at \(1.8 × 10^{−3}\) shows it is better because it remains stable for larger learning rates and even attains a slightly lower validation loss. This is confirmed in Figure 10b which shows a slightly improved accuracy at learning rates above 0.005.

一个合理的问题是权重衰减值、学习率和动量都可以同时确定吗？图10a显示了在不同的学习率(LR = 0.001 - 0.01 )，以及递减的动量(= 0.98 - 0.8)下执行\(10^{-2}, 3.2×10^{−3}, 10^{−3}\)的权重衰减测试。和以前一样，\(3.2× 10^{−3}\)的实现似乎是最好的。然而，对\(1.8× 10^{−3}\)大小的权重衰减测试表明，它在较大的学习率下保持稳定，甚至获得了略低的验证损失。这在图10b中得到证实

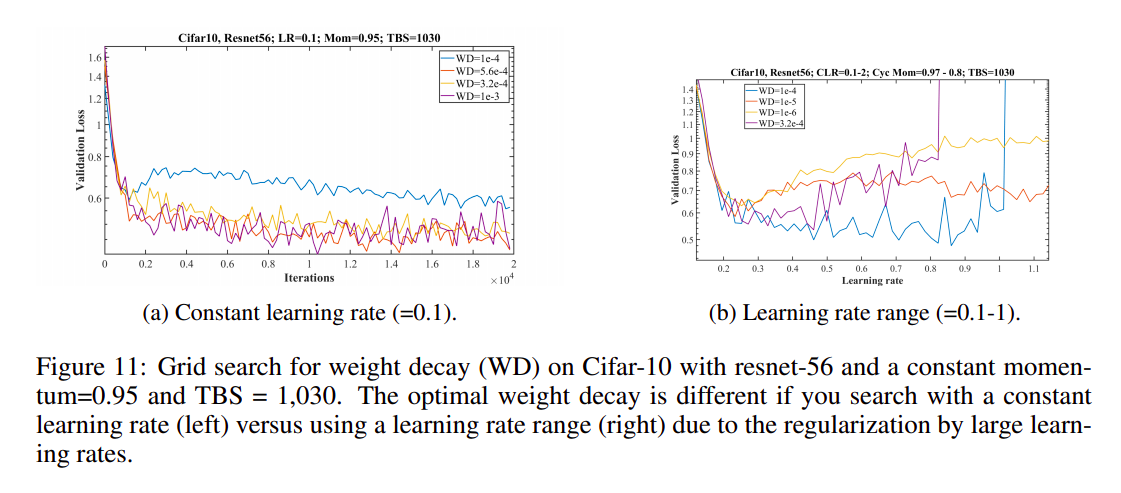
The optimal weight decay is different if you search with a constant learning rate versus using a learning rate range. This aligns with our intuition because the larger learning rates provide regularization so a smaller weight decay value is optimal. Figure 11a shows the results of a weight decay search with a constant learning rate of 0.1. In this case a weight decay of \(10^{−4}\) exhibits overfitting and a larger weight decay of \(10^{−3}\) is better. Also shown are the similar results at weight decays of \(3.2 × 10^{−4}\) and \(5.6 × 10^{−4}\) to illustrate that a single significant figure accuracy for weight decay is all that is necessary. On the other hand, Figure 11b illustrates the results of a weight decay search using a learning rate range test from 0.1 to 1.0. This search indicates a smaller weight decay value of \(10^{−4}\) is best and larger learning rates in the range of 0.5 to 0.8 should be used.

如果你用一个恒定的学习率搜索和用一个学习率范围搜索，最佳的权重衰减是不同的。这与我们的直觉一致，因为更高的学习率提供了正则化，所以更小的权重衰减值是最佳的。图11a显示了恒定学习率为0.1的权重衰减搜索结果。在这种情况下，\(10^{−4}\)的权重衰减表现出过拟合，\(10^{−3}\)的权重衰减看起来更好。图中还显示了权重衰减为\(3.2 × 10^{−4}\)和\(5.6 × 10^{−4}\)时的类似结果，说明固定有效精度的权重衰减是必要的。另一方面，图11b显示了使用从0.1到1.0的学习率范围测试的权重衰减搜索的结果。该搜索表明更小的\(10^{−4}\)权重衰减值是最好的，并且应该使用0.5到0.8范围内的较大学习率

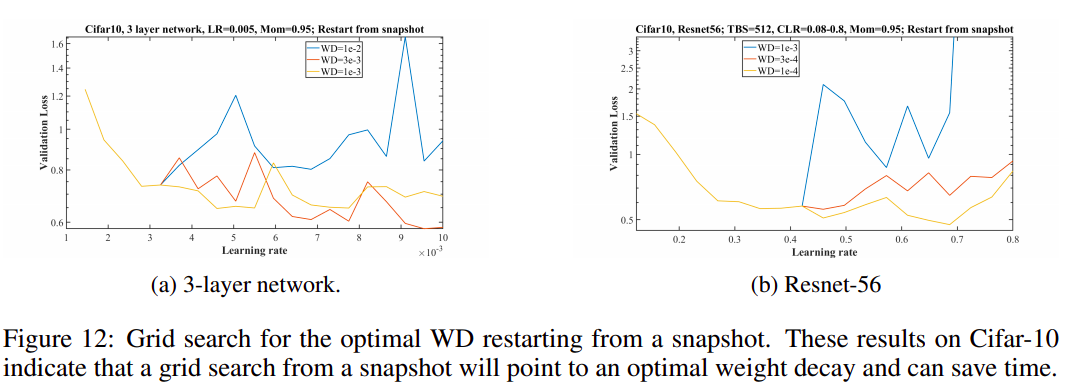
Another option as a grid search for weight decay is to make a single run at a middle value for weight decay and save a snapshot after the loss plateaus. Use this snapshot to restart runs, each with a different value of WD. This can save time in searching for the best weight decay. Figure 12a shows an example on Cifar-10 with a 3-layer network (this is for illustration only as this architecture runs very quickly). Here the initial run was with a sub-optimal value of weight decay of \(10^{−3}\) . From the restart point, three continuation runs were made with weight decay values of \(10^{−3} , 3 × 10^{−3}\), and \(10^{−2}\). This Figure shows that \(3 × 10^{−3}\) is best.

还有一个权重衰减网格搜索的设置是在权重衰减的中间值运行一次，并在损失稳定后保存一个快照。使用此快照重新启动运行，每个运行都具有不同的WD(weight decay)值。这可以节省寻找最佳权重衰减的时间。图12a显示了具有3层网络的Cifar-10示例（这只是为了说明，因为该架构运行非常快)。在这里，最初的运行是使用次优值，\(10^{−3}\)大小权重衰减。从重启点开始，用\(10^{−3}、3 × 10^{−3}\)和\(10^{−2}\)的权重衰减值进行了三次连续运行，这个数字表明\(3× 10^{−3}\)是最好的

Figure 12b illustrates a weight decay grid search from a snapshot for resnet-56 while performing a LR range test. This Figure shows the first half of the range test with a value of weight decay of \(10^{−4}\) . Then three continuations are run with weight decay values of \(10^{−3}, 3 × 10^{−4}\), and \(10^{−4}\) . It is clear that a weight decay value of \(10^{−4}\) is best and information about the learning rate range is simultaneously available.

图12b显示了在执行LR范围测试时从resnet-56的快照中进行的权重衰减网格搜索。该图显示了权重衰减值为\(10^{−4}\)的范围试验的前半部分。然后用\(10^{−3}、3 × 10^{−4}\)和\(10^{−4}\)的权重衰减值进行测试。很明显，\(10^{−4}\)的权重衰减值是最佳的，并且关于学习率范围的信息是可用的

实现流程

根据论文描述，以及参考All the other parameters matter。寻找最优权重衰减值的实现流程如下：

找到最优学习率
固定学习率，测试0/1e-3/1e-4/1e-5大小的权重衰减
比如找到了1e-4，再进一步测试3e-5/1e-4/3e-4大小的权重衰减
得到最佳权重衰减值

PyTorch实现

首先参考[LR Scheduler]如何找到最优学习率找到最优学习率，然后进一步测试权重衰减值。完整代码参考：find_wd.py

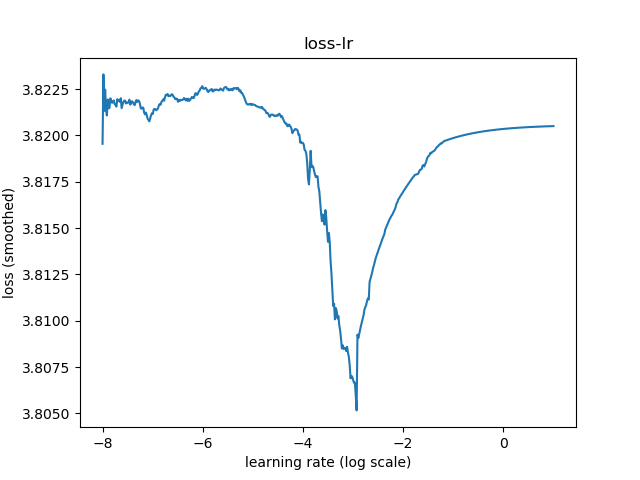
训练参数

模型：SqueezeNet
数据集：CIFAR100
损失函数：标签平滑正则化
优化器：Adam
批量大小：96
学习率：最小学习率1e-8，最高学习率10

最优学习率

执行py/lr/find_lr.py：

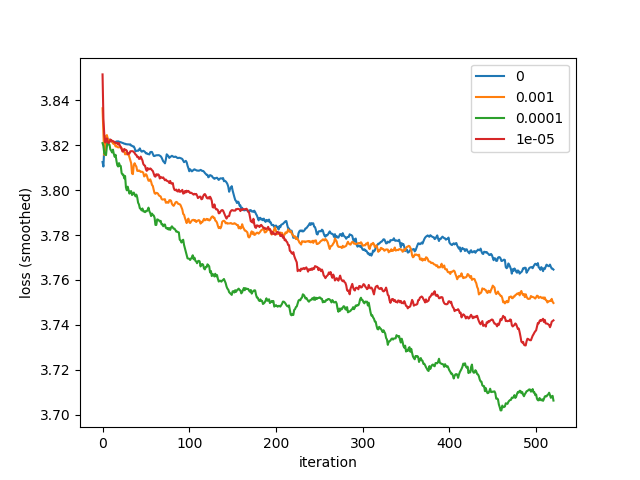
0/1e-3/1e-4/1e-5

得到最优学习率3e-4后，进一步测试不同的权重衰减值。执行py/lr/find_wd.py

根据训练结果可知1e-4具有更好的正则化效果

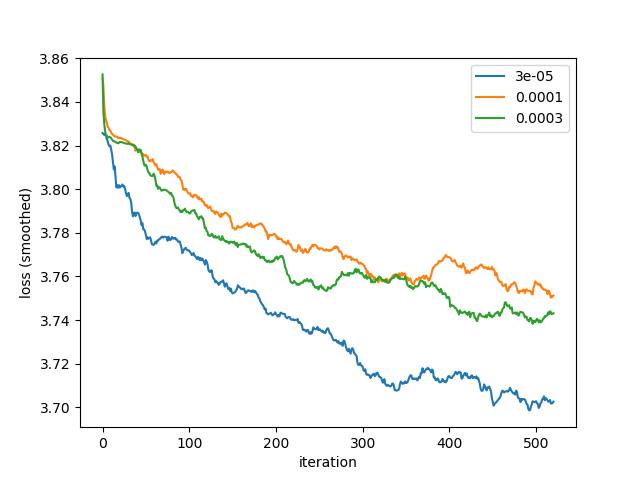
3e-5/1e-4/3e-4

进一步测试，得到结果如下：

从训练结果来看，3e-5提供了更低的训练损失

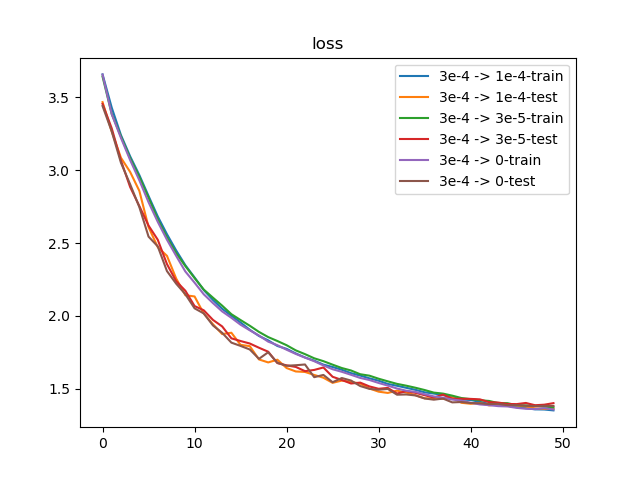
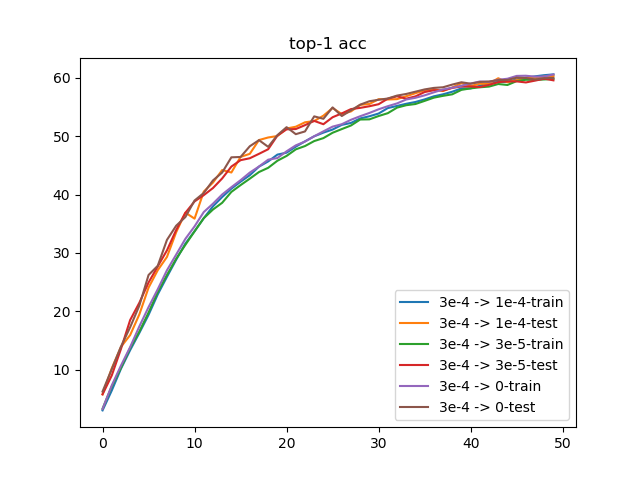
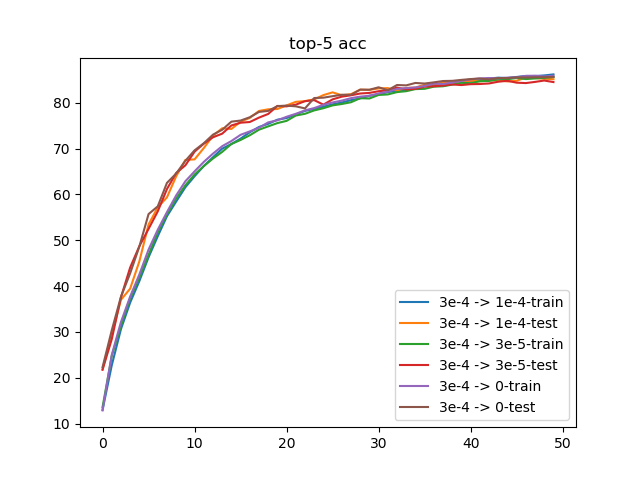
不同范围的学习率衰减比较

在训练过程中，常用的学习率调度方式是warmup + CosineAnnealing。从上面实验中，已确定了最优的学习率和权重衰减值分别为3e-4和3e-5，下面比较不同的学习率衰减范围：

3e-4 -> 1e-4
3e-4 -> 3e-5
3e-4 -> 0

执行文件py/lr/train_wd.py，训练50轮结果如下：

3e-4 -> 1e-4
- Top-1 acc: 60.31%
- Top-5 acc: 85.53%
3e-4 -> 3e-5
- Top-1 acc: 59.85%
- Top-5 acc: 84.86%
3e-4 -> 0
- Top-1 acc: 60.02%
- Top-5 acc: 85.64%

从训练结果来看，3种学习率范围得到的损失值和准确度非常接近。综合Top-1和Top-5准确度来说，采用3e-4 -> 1e-4能够得到比较均衡的结果

小结

对于任何的数据集和网络模型，可以按照上述的训练方式得到最优的学习率和权重衰减值

对于Adam优化器而言，可以默认设置

学习率为3e-4
学习率衰减范围为3e-4 -> 1e-4
权重衰减值为3e-5

Appendix

不同学习率范围的训练日志如下：

$ python train_wd.py 
Files already downloaded and verified
Files already downloaded and verified
{'train': <torch.utils.data.dataloader.DataLoader object at 0x7f393568bf10>, 'test': <torch.utils.data.dataloader.DataLoader object at 0x7f393b519ad0>}
{'train': 50000, 'test': 10000}
3e-4 -> 1e-4 - Epoch 1/50
----------
lr: 5.9999999999999995e-05
train Loss: 3.6565 Top-1 Acc: 3.0106 Top-5 Acc: 12.9986
test Loss: 3.4664 Top-1 Acc: 5.7715 Top-5 Acc: 21.8900
3e-4 -> 1e-4 - Epoch 2/50
----------
lr: 0.00011999999999999999
train Loss: 3.4280 Top-1 Acc: 6.4111 Top-5 Acc: 22.7103
test Loss: 3.2642 Top-1 Acc: 10.2073 Top-5 Acc: 29.4159
3e-4 -> 1e-4 - Epoch 3/50
----------
lr: 0.00017999999999999998
train Loss: 3.2401 Top-1 Acc: 10.1428 Top-5 Acc: 30.6198
test Loss: 3.0847 Top-1 Acc: 13.8856 Top-5 Acc: 37.0215
3e-4 -> 1e-4 - Epoch 4/50
----------
lr: 0.00023999999999999998
train Loss: 3.0944 Top-1 Acc: 13.3373 Top-5 Acc: 36.4116
test Loss: 2.9874 Top-1 Acc: 15.9191 Top-5 Acc: 39.4537
3e-4 -> 1e-4 - Epoch 5/50
----------
lr: 0.0003
/home/lab305/anaconda3/envs/pytorch1.5/lib/python3.7/site-packages/torch/optim/lr_scheduler.py:484: UserWarning: To get the last learning rate computed by the scheduler, please use `get_last_lr()`.
  "please use `get_last_lr()`.", UserWarning)
train Loss: 2.9657 Top-1 Acc: 16.2908 Top-5 Acc: 41.0992
test Loss: 2.8573 Top-1 Acc: 19.4577 Top-5 Acc: 45.4047
3e-4 -> 1e-4 - Epoch 6/50
----------
lr: 0.0003
train Loss: 2.8223 Top-1 Acc: 19.3838 Top-5 Acc: 46.3016
test Loss: 2.6091 Top-1 Acc: 24.0431 Top-5 Acc: 53.4490
3e-4 -> 1e-4 - Epoch 7/50
----------
lr: 0.0002997564050259824
train Loss: 2.6824 Top-1 Acc: 22.8939 Top-5 Acc: 50.8941
test Loss: 2.4715 Top-1 Acc: 27.0335 Top-5 Acc: 57.1970
3e-4 -> 1e-4 - Epoch 8/50
----------
lr: 0.00029902680687415704
train Loss: 2.5606 Top-1 Acc: 25.8997 Top-5 Acc: 55.2539
test Loss: 2.4121 Top-1 Acc: 29.3062 Top-5 Acc: 59.3700
3e-4 -> 1e-4 - Epoch 9/50
----------
lr: 0.00029781476007338057
train Loss: 2.4491 Top-1 Acc: 28.8240 Top-5 Acc: 58.4541
test Loss: 2.2567 Top-1 Acc: 33.5327 Top-5 Acc: 63.9653
3e-4 -> 1e-4 - Epoch 10/50
----------
lr: 0.0002961261695938319
train Loss: 2.3476 Top-1 Acc: 31.5895 Top-5 Acc: 61.5715
test Loss: 2.1420 Top-1 Acc: 36.9019 Top-5 Acc: 67.5339
3e-4 -> 1e-4 - Epoch 11/50
----------
lr: 0.00029396926207859086
train Loss: 2.2638 Top-1 Acc: 33.7108 Top-5 Acc: 63.9775
test Loss: 2.1335 Top-1 Acc: 35.8652 Top-5 Acc: 67.6535
3e-4 -> 1e-4 - Epoch 12/50
----------
lr: 0.0002913545457642601
train Loss: 2.1775 Top-1 Acc: 35.9481 Top-5 Acc: 66.2028
test Loss: 2.0162 Top-1 Acc: 40.5004 Top-5 Acc: 70.1156
3e-4 -> 1e-4 - Epoch 13/50
----------
lr: 0.0002882947592858927
train Loss: 2.1094 Top-1 Acc: 37.9766 Top-5 Acc: 68.1186
test Loss: 1.9429 Top-1 Acc: 42.0455 Top-5 Acc: 72.8170
3e-4 -> 1e-4 - Epoch 14/50
----------
lr: 0.0002848048096156426
train Loss: 2.0494 Top-1 Acc: 39.5729 Top-5 Acc: 69.9944
test Loss: 1.8755 Top-1 Acc: 44.1886 Top-5 Acc: 74.4418
3e-4 -> 1e-4 - Epoch 15/50
----------
lr: 0.00028090169943749475
train Loss: 2.0007 Top-1 Acc: 41.0065 Top-5 Acc: 71.0029
test Loss: 1.8846 Top-1 Acc: 43.7699 Top-5 Acc: 74.2923
3e-4 -> 1e-4 - Epoch 16/50
----------
lr: 0.0002766044443118978
train Loss: 1.9548 Top-1 Acc: 42.1941 Top-5 Acc: 72.1805
test Loss: 1.8015 Top-1 Acc: 46.4414 Top-5 Acc: 75.8772
3e-4 -> 1e-4 - Epoch 17/50
----------
lr: 0.0002719339800338651
train Loss: 1.9051 Top-1 Acc: 43.3046 Top-5 Acc: 73.5680
test Loss: 1.7927 Top-1 Acc: 46.9697 Top-5 Acc: 76.7045
3e-4 -> 1e-4 - Epoch 18/50
----------
lr: 0.0002669130606358858
train Loss: 1.8625 Top-1 Acc: 44.7773 Top-5 Acc: 74.7221
test Loss: 1.7015 Top-1 Acc: 49.3321 Top-5 Acc: 78.2197
3e-4 -> 1e-4 - Epoch 19/50
----------
lr: 0.00026156614753256583
train Loss: 1.8324 Top-1 Acc: 45.6722 Top-5 Acc: 75.4123
test Loss: 1.6811 Top-1 Acc: 49.7707 Top-5 Acc: 78.5786
3e-4 -> 1e-4 - Epoch 20/50
----------
lr: 0.0002559192903470747
train Loss: 1.7939 Top-1 Acc: 46.8346 Top-5 Acc: 76.3100
test Loss: 1.6998 Top-1 Acc: 50.0199 Top-5 Acc: 78.6483
3e-4 -> 1e-4 - Epoch 21/50
----------
lr: 0.00025
train Loss: 1.7743 Top-1 Acc: 47.1697 Top-5 Acc: 76.6755
test Loss: 1.6427 Top-1 Acc: 51.3058 Top-5 Acc: 79.4258
3e-4 -> 1e-4 - Epoch 22/50
----------
lr: 0.00024383711467890776
train Loss: 1.7427 Top-1 Acc: 48.1958 Top-5 Acc: 77.4487
test Loss: 1.6191 Top-1 Acc: 51.6148 Top-5 Acc: 80.2033
3e-4 -> 1e-4 - Epoch 23/50
----------
lr: 0.00023746065934159125
train Loss: 1.7150 Top-1 Acc: 49.1059 Top-5 Acc: 78.2326
test Loss: 1.6158 Top-1 Acc: 52.3724 Top-5 Acc: 80.3728
3e-4 -> 1e-4 - Epoch 24/50
----------
lr: 0.00023090169943749478
train Loss: 1.6934 Top-1 Acc: 49.9720 Top-5 Acc: 78.6632
test Loss: 1.5954 Top-1 Acc: 52.5917 Top-5 Acc: 80.7416
3e-4 -> 1e-4 - Epoch 25/50
----------
lr: 0.00022419218955996686
train Loss: 1.6660 Top-1 Acc: 50.6014 Top-5 Acc: 79.1514
test Loss: 1.5762 Top-1 Acc: 53.5088 Top-5 Acc: 81.6786
3e-4 -> 1e-4 - Epoch 26/50
----------
lr: 0.00021736481776669312
train Loss: 1.6498 Top-1 Acc: 51.1313 Top-5 Acc: 79.6661
test Loss: 1.5411 Top-1 Acc: 54.8146 Top-5 Acc: 82.2767
3e-4 -> 1e-4 - Epoch 27/50
----------
lr: 0.00021045284632676542
train Loss: 1.6308 Top-1 Acc: 51.9318 Top-5 Acc: 80.0668
test Loss: 1.5566 Top-1 Acc: 53.7879 Top-5 Acc: 81.6487
3e-4 -> 1e-4 - Epoch 28/50
----------
lr: 0.00020348994967025018
train Loss: 1.6077 Top-1 Acc: 52.2637 Top-5 Acc: 80.5798
test Loss: 1.5477 Top-1 Acc: 54.2364 Top-5 Acc: 81.8780
3e-4 -> 1e-4 - Epoch 29/50
----------
lr: 0.00019651005032975
train Loss: 1.5910 Top-1 Acc: 53.0358 Top-5 Acc: 80.9673
test Loss: 1.5356 Top-1 Acc: 55.3628 Top-5 Acc: 82.8648
3e-4 -> 1e-4 - Epoch 30/50
----------
lr: 0.00018954715367323473
train Loss: 1.5720 Top-1 Acc: 53.4053 Top-5 Acc: 81.5307
test Loss: 1.5025 Top-1 Acc: 55.5124 Top-5 Acc: 82.8250
3e-4 -> 1e-4 - Epoch 31/50
----------
lr: 0.00018263518223330703
train Loss: 1.5558 Top-1 Acc: 53.8740 Top-5 Acc: 81.8086
test Loss: 1.4806 Top-1 Acc: 56.3297 Top-5 Acc: 83.1340
3e-4 -> 1e-4 - Epoch 32/50
----------
lr: 0.00017580781044003327
train Loss: 1.5336 Top-1 Acc: 54.8093 Top-5 Acc: 82.3433
test Loss: 1.4719 Top-1 Acc: 56.2799 Top-5 Acc: 83.2037
3e-4 -> 1e-4 - Epoch 33/50
----------
lr: 0.00016909830056250532
train Loss: 1.5210 Top-1 Acc: 55.1751 Top-5 Acc: 82.6000
test Loss: 1.4874 Top-1 Acc: 56.3397 Top-5 Acc: 82.6755
3e-4 -> 1e-4 - Epoch 34/50
----------
lr: 0.00016253934065840883
train Loss: 1.5071 Top-1 Acc: 55.5466 Top-5 Acc: 82.7591
test Loss: 1.4750 Top-1 Acc: 56.8381 Top-5 Acc: 83.2436
3e-4 -> 1e-4 - Epoch 35/50
----------
lr: 0.00015616288532109226
train Loss: 1.4932 Top-1 Acc: 55.8513 Top-5 Acc: 83.2049
test Loss: 1.4561 Top-1 Acc: 57.3564 Top-5 Acc: 83.3234
3e-4 -> 1e-4 - Epoch 36/50
----------
lr: 0.00015000000000000004
train Loss: 1.4762 Top-1 Acc: 56.2956 Top-5 Acc: 83.7716
test Loss: 1.4352 Top-1 Acc: 57.8449 Top-5 Acc: 83.9414
3e-4 -> 1e-4 - Epoch 37/50
----------
lr: 0.00014408070965292533
train Loss: 1.4676 Top-1 Acc: 56.8222 Top-5 Acc: 83.6948
test Loss: 1.4333 Top-1 Acc: 58.0243 Top-5 Acc: 83.9713
3e-4 -> 1e-4 - Epoch 38/50
----------
lr: 0.0001384338524674342
train Loss: 1.4576 Top-1 Acc: 57.1653 Top-5 Acc: 83.6800
test Loss: 1.4306 Top-1 Acc: 57.7253 Top-5 Acc: 84.4298
3e-4 -> 1e-4 - Epoch 39/50
----------
lr: 0.0001330869393641142
train Loss: 1.4418 Top-1 Acc: 57.6088 Top-5 Acc: 84.2434
test Loss: 1.4435 Top-1 Acc: 58.3333 Top-5 Acc: 84.3302
3e-4 -> 1e-4 - Epoch 40/50
----------
lr: 0.0001280660199661349
train Loss: 1.4270 Top-1 Acc: 58.1754 Top-5 Acc: 84.5626
test Loss: 1.4042 Top-1 Acc: 59.0809 Top-5 Acc: 84.5594
3e-4 -> 1e-4 - Epoch 41/50
----------
lr: 0.00012339555568810222
train Loss: 1.4234 Top-1 Acc: 58.1830 Top-5 Acc: 84.6145
test Loss: 1.3977 Top-1 Acc: 58.5925 Top-5 Acc: 84.8086
3e-4 -> 1e-4 - Epoch 42/50
----------
lr: 0.00011909830056250527
train Loss: 1.4107 Top-1 Acc: 58.6280 Top-5 Acc: 84.9112
test Loss: 1.4022 Top-1 Acc: 58.9713 Top-5 Acc: 84.6890
3e-4 -> 1e-4 - Epoch 43/50
----------
lr: 0.0001151951903843574
train Loss: 1.3962 Top-1 Acc: 59.1143 Top-5 Acc: 85.2875
test Loss: 1.3866 Top-1 Acc: 58.9912 Top-5 Acc: 84.8784
3e-4 -> 1e-4 - Epoch 44/50
----------
lr: 0.00011170524071410733
train Loss: 1.3891 Top-1 Acc: 59.2922 Top-5 Acc: 85.4831
test Loss: 1.3929 Top-1 Acc: 59.9183 Top-5 Acc: 84.9183
3e-4 -> 1e-4 - Epoch 45/50
----------
lr: 0.00010864545423573992
train Loss: 1.3842 Top-1 Acc: 59.2958 Top-5 Acc: 85.4070
test Loss: 1.3918 Top-1 Acc: 59.2305 Top-5 Acc: 84.6591
3e-4 -> 1e-4 - Epoch 46/50
----------
lr: 0.00010603073792140917
train Loss: 1.3739 Top-1 Acc: 59.7137 Top-5 Acc: 85.6362
test Loss: 1.3854 Top-1 Acc: 59.5893 Top-5 Acc: 84.8086
3e-4 -> 1e-4 - Epoch 47/50
----------
lr: 0.00010387383040616813
train Loss: 1.3679 Top-1 Acc: 59.9856 Top-5 Acc: 85.8586
test Loss: 1.3785 Top-1 Acc: 59.9980 Top-5 Acc: 85.5263
3e-4 -> 1e-4 - Epoch 48/50
----------
lr: 0.00010218523992661944
train Loss: 1.3593 Top-1 Acc: 60.2471 Top-5 Acc: 85.8306
test Loss: 1.3656 Top-1 Acc: 59.9083 Top-5 Acc: 85.4067
3e-4 -> 1e-4 - Epoch 49/50
----------
lr: 0.00010097319312584298
train Loss: 1.3582 Top-1 Acc: 60.4459 Top-5 Acc: 85.9729
test Loss: 1.3629 Top-1 Acc: 60.2073 Top-5 Acc: 85.2472
3e-4 -> 1e-4 - Epoch 50/50
----------
lr: 0.00010024359497401759
train Loss: 1.3521 Top-1 Acc: 60.5786 Top-5 Acc: 86.1952
test Loss: 1.3635 Top-1 Acc: 60.3070 Top-5 Acc: 85.1475
Training 3e-4 -> 1e-4 complete in 147m 31s
Best test Top-1 Acc: 60.307045
Best test Top-5 Acc: 85.526329
train 3e-4 -> 1e-4 done

3e-4 -> 3e-5 - Epoch 1/50
----------
lr: 5.9999999999999995e-05
train Loss: 3.6414 Top-1 Acc: 3.2969 Top-5 Acc: 13.6081
test Loss: 3.4543 Top-1 Acc: 5.7516 Top-5 Acc: 21.7504
3e-4 -> 3e-5 - Epoch 2/50
----------
lr: 0.00011999999999999999
train Loss: 3.3848 Top-1 Acc: 7.1181 Top-5 Acc: 24.7533
test Loss: 3.2861 Top-1 Acc: 8.9912 Top-5 Acc: 28.4191
3e-4 -> 3e-5 - Epoch 3/50
----------
lr: 0.00017999999999999998
train Loss: 3.2303 Top-1 Acc: 10.3059 Top-5 Acc: 31.3844
test Loss: 3.0654 Top-1 Acc: 13.5367 Top-5 Acc: 37.5598
3e-4 -> 3e-5 - Epoch 4/50
----------
lr: 0.00023999999999999998
train Loss: 3.0817 Top-1 Acc: 13.7008 Top-5 Acc: 37.3828
test Loss: 2.8840 Top-1 Acc: 18.4908 Top-5 Acc: 44.0590
3e-4 -> 3e-5 - Epoch 5/50
----------
lr: 0.0003
train Loss: 2.9535 Top-1 Acc: 16.5207 Top-5 Acc: 41.8986
test Loss: 2.7533 Top-1 Acc: 21.4514 Top-5 Acc: 48.7241
3e-4 -> 3e-5 - Epoch 6/50
----------
lr: 0.0003
train Loss: 2.8102 Top-1 Acc: 19.7821 Top-5 Acc: 46.8246
test Loss: 2.6194 Top-1 Acc: 24.9202 Top-5 Acc: 52.4821
3e-4 -> 3e-5 - Epoch 7/50
----------
lr: 0.0002996711467850762
train Loss: 2.6619 Top-1 Acc: 23.2945 Top-5 Acc: 51.7534
test Loss: 2.5225 Top-1 Acc: 27.6914 Top-5 Acc: 56.3098
3e-4 -> 3e-5 - Epoch 8/50
----------
lr: 0.0002986861892801119
train Loss: 2.5392 Top-1 Acc: 26.2208 Top-5 Acc: 55.6966
test Loss: 2.3555 Top-1 Acc: 30.4326 Top-5 Acc: 61.1842
3e-4 -> 3e-5 - Epoch 9/50
----------
lr: 0.0002970499260990637
train Loss: 2.4308 Top-1 Acc: 28.9879 Top-5 Acc: 59.1323
test Loss: 2.2380 Top-1 Acc: 33.9214 Top-5 Acc: 64.6830
3e-4 -> 3e-5 - Epoch 10/50
----------
lr: 0.000294770328951673
train Loss: 2.3416 Top-1 Acc: 31.3792 Top-5 Acc: 61.9942
test Loss: 2.1727 Top-1 Acc: 36.8620 Top-5 Acc: 66.3577
3e-4 -> 3e-5 - Epoch 11/50
----------
lr: 0.0002918585038060976
train Loss: 2.2597 Top-1 Acc: 33.6912 Top-5 Acc: 64.3566
test Loss: 2.0676 Top-1 Acc: 38.8158 Top-5 Acc: 69.3381
3e-4 -> 3e-5 - Epoch 12/50
----------
lr: 0.0002883286367817511
train Loss: 2.1806 Top-1 Acc: 35.9409 Top-5 Acc: 66.1784
test Loss: 2.0385 Top-1 Acc: 39.8923 Top-5 Acc: 71.0726
3e-4 -> 3e-5 - Epoch 13/50
----------
lr: 0.00028419792503595515
train Loss: 2.1250 Top-1 Acc: 37.4288 Top-5 Acc: 67.8439
test Loss: 1.9726 Top-1 Acc: 41.1085 Top-5 Acc: 72.4781
3e-4 -> 3e-5 - Epoch 14/50
----------
lr: 0.0002794864929811175
train Loss: 2.0703 Top-1 Acc: 38.5816 Top-5 Acc: 69.2831
test Loss: 1.9279 Top-1 Acc: 42.7532 Top-5 Acc: 73.2656
3e-4 -> 3e-5 - Epoch 15/50
----------
lr: 0.0002742172942406179
train Loss: 2.0119 Top-1 Acc: 40.4490 Top-5 Acc: 71.0157
test Loss: 1.8464 Top-1 Acc: 44.7867 Top-5 Acc: 75.0499
3e-4 -> 3e-5 - Epoch 16/50
----------
lr: 0.000268415999821062
train Loss: 1.9717 Top-1 Acc: 41.6107 Top-5 Acc: 71.8878
test Loss: 1.8279 Top-1 Acc: 45.8832 Top-5 Acc: 75.6579
3e-4 -> 3e-5 - Epoch 17/50
----------
lr: 0.00026211087304571794
train Loss: 1.9326 Top-1 Acc: 42.7115 Top-5 Acc: 72.9163
test Loss: 1.8109 Top-1 Acc: 46.2121 Top-5 Acc: 75.8074
3e-4 -> 3e-5 - Epoch 18/50
----------
lr: 0.0002553326318584459
train Loss: 1.8903 Top-1 Acc: 43.8511 Top-5 Acc: 74.1303
test Loss: 1.7818 Top-1 Acc: 46.9697 Top-5 Acc: 76.7643
3e-4 -> 3e-5 - Epoch 19/50
----------
lr: 0.0002481142991689639
train Loss: 1.8549 Top-1 Acc: 44.5733 Top-5 Acc: 74.8617
test Loss: 1.7546 Top-1 Acc: 47.7572 Top-5 Acc: 77.5618
3e-4 -> 3e-5 - Epoch 20/50
----------
lr: 0.00024049104196855088
train Loss: 1.8279 Top-1 Acc: 45.7837 Top-5 Acc: 75.5722
test Loss: 1.6767 Top-1 Acc: 50.0897 Top-5 Acc: 79.3162
3e-4 -> 3e-5 - Epoch 21/50
----------
lr: 0.00023250000000000007
train Loss: 1.7992 Top-1 Acc: 46.6127 Top-5 Acc: 76.0604
test Loss: 1.6609 Top-1 Acc: 51.1663 Top-5 Acc: 79.2265
3e-4 -> 3e-5 - Epoch 22/50
----------
lr: 0.00022418010481652553
train Loss: 1.7637 Top-1 Acc: 47.7375 Top-5 Acc: 77.2188
test Loss: 1.6502 Top-1 Acc: 51.2161 Top-5 Acc: 79.5953
3e-4 -> 3e-5 - Epoch 23/50
----------
lr: 0.00021557189011114819
train Loss: 1.7379 Top-1 Acc: 48.3017 Top-5 Acc: 77.5992
test Loss: 1.6212 Top-1 Acc: 51.8840 Top-5 Acc: 80.3529
3e-4 -> 3e-5 - Epoch 24/50
----------
lr: 0.000206717294240618
train Loss: 1.7095 Top-1 Acc: 49.1551 Top-5 Acc: 78.3406
test Loss: 1.6296 Top-1 Acc: 52.6116 Top-5 Acc: 80.5821
3e-4 -> 3e-5 - Epoch 25/50
----------
lr: 0.00019765945590595523
train Loss: 1.6897 Top-1 Acc: 49.6629 Top-5 Acc: 78.8195
test Loss: 1.6464 Top-1 Acc: 52.0434 Top-5 Acc: 79.5953
3e-4 -> 3e-5 - Epoch 26/50
----------
lr: 0.00018844250398503568
train Loss: 1.6658 Top-1 Acc: 50.5818 Top-5 Acc: 79.4345
test Loss: 1.5826 Top-1 Acc: 53.2396 Top-5 Acc: 80.7516
3e-4 -> 3e-5 - Epoch 27/50
----------
lr: 0.0001791113425411333
train Loss: 1.6426 Top-1 Acc: 51.2120 Top-5 Acc: 79.7401
test Loss: 1.5609 Top-1 Acc: 53.8975 Top-5 Acc: 81.3397
3e-4 -> 3e-5 - Epoch 28/50
----------
lr: 0.00016971143205483772
train Loss: 1.6258 Top-1 Acc: 51.8274 Top-5 Acc: 80.1208
test Loss: 1.5366 Top-1 Acc: 54.6352 Top-5 Acc: 81.6387
3e-4 -> 3e-5 - Epoch 29/50
----------
lr: 0.00016028856794516246
train Loss: 1.6001 Top-1 Acc: 52.8483 Top-5 Acc: 81.0005
test Loss: 1.5426 Top-1 Acc: 54.8445 Top-5 Acc: 82.0275
3e-4 -> 3e-5 - Epoch 30/50
----------
lr: 0.00015088865745886687
train Loss: 1.5902 Top-1 Acc: 52.8779 Top-5 Acc: 80.9405
test Loss: 1.5166 Top-1 Acc: 55.1236 Top-5 Acc: 82.1571
3e-4 -> 3e-5 - Epoch 31/50
----------
lr: 0.00014155749601496448
train Loss: 1.5694 Top-1 Acc: 53.4465 Top-5 Acc: 81.7094
test Loss: 1.5004 Top-1 Acc: 55.4725 Top-5 Acc: 82.5259
3e-4 -> 3e-5 - Epoch 32/50
----------
lr: 0.0001323405440940449
train Loss: 1.5513 Top-1 Acc: 53.9340 Top-5 Acc: 81.8246
test Loss: 1.5062 Top-1 Acc: 56.4195 Top-5 Acc: 82.7053
3e-4 -> 3e-5 - Epoch 33/50
----------
lr: 0.00012328270575938217
train Loss: 1.5340 Top-1 Acc: 54.8840 Top-5 Acc: 82.3336
test Loss: 1.4675 Top-1 Acc: 56.8281 Top-5 Acc: 83.3234
3e-4 -> 3e-5 - Epoch 34/50
----------
lr: 0.00011442810988885193
train Loss: 1.5216 Top-1 Acc: 55.2999 Top-5 Acc: 82.5348
test Loss: 1.4839 Top-1 Acc: 56.4195 Top-5 Acc: 82.9246
3e-4 -> 3e-5 - Epoch 35/50
----------
lr: 0.00010581989518347459
train Loss: 1.5075 Top-1 Acc: 55.5034 Top-5 Acc: 82.9870
test Loss: 1.4727 Top-1 Acc: 56.8082 Top-5 Acc: 83.0443
3e-4 -> 3e-5 - Epoch 36/50
----------
lr: 9.750000000000008e-05
train Loss: 1.4918 Top-1 Acc: 56.0405 Top-5 Acc: 83.0463
test Loss: 1.4564 Top-1 Acc: 57.5558 Top-5 Acc: 83.5127
3e-4 -> 3e-5 - Epoch 37/50
----------
lr: 8.950895803144924e-05
train Loss: 1.4741 Top-1 Acc: 56.5935 Top-5 Acc: 83.5209
test Loss: 1.4399 Top-1 Acc: 57.8648 Top-5 Acc: 83.6025
3e-4 -> 3e-5 - Epoch 38/50
----------
lr: 8.188570083103617e-05
train Loss: 1.4672 Top-1 Acc: 56.9050 Top-5 Acc: 83.6077
test Loss: 1.4603 Top-1 Acc: 57.8250 Top-5 Acc: 83.7619
3e-4 -> 3e-5 - Epoch 39/50
----------
lr: 7.466736814155417e-05
train Loss: 1.4533 Top-1 Acc: 57.1661 Top-5 Acc: 83.9671
test Loss: 1.4323 Top-1 Acc: 58.2635 Top-5 Acc: 84.0012
3e-4 -> 3e-5 - Epoch 40/50
----------
lr: 6.788912695428212e-05
train Loss: 1.4369 Top-1 Acc: 57.9295 Top-5 Acc: 84.3522
test Loss: 1.4316 Top-1 Acc: 58.5128 Top-5 Acc: 83.8716
3e-4 -> 3e-5 - Epoch 41/50
----------
lr: 6.158400017893801e-05
train Loss: 1.4295 Top-1 Acc: 58.1862 Top-5 Acc: 84.2662
test Loss: 1.4310 Top-1 Acc: 58.5028 Top-5 Acc: 84.0610
3e-4 -> 3e-5 - Epoch 42/50
----------
lr: 5.578270575938213e-05
train Loss: 1.4217 Top-1 Acc: 58.3705 Top-5 Acc: 84.7137
test Loss: 1.4278 Top-1 Acc: 58.4131 Top-5 Acc: 84.1009
3e-4 -> 3e-5 - Epoch 43/50
----------
lr: 5.0513507018882515e-05
train Loss: 1.4170 Top-1 Acc: 58.4913 Top-5 Acc: 84.7669
test Loss: 1.4087 Top-1 Acc: 58.7819 Top-5 Acc: 84.2205
3e-4 -> 3e-5 - Epoch 44/50
----------
lr: 4.5802074964044906e-05
train Loss: 1.4020 Top-1 Acc: 58.9319 Top-5 Acc: 85.1199
test Loss: 1.4059 Top-1 Acc: 59.2504 Top-5 Acc: 84.5993
3e-4 -> 3e-5 - Epoch 45/50
----------
lr: 4.1671363218248916e-05
train Loss: 1.4015 Top-1 Acc: 58.7668 Top-5 Acc: 85.1348
test Loss: 1.3962 Top-1 Acc: 59.3800 Top-5 Acc: 84.7987
3e-4 -> 3e-5 - Epoch 46/50
----------
lr: 3.8141496193902386e-05
train Loss: 1.3877 Top-1 Acc: 59.4310 Top-5 Acc: 85.4167
test Loss: 1.3952 Top-1 Acc: 59.3800 Top-5 Acc: 84.3899
3e-4 -> 3e-5 - Epoch 47/50
----------
lr: 3.5229671048326984e-05
train Loss: 1.3858 Top-1 Acc: 59.6605 Top-5 Acc: 85.1751
test Loss: 1.4032 Top-1 Acc: 59.2006 Top-5 Acc: 84.3002
3e-4 -> 3e-5 - Epoch 48/50
----------
lr: 3.2950073900936234e-05
train Loss: 1.3844 Top-1 Acc: 59.6441 Top-5 Acc: 85.3111
test Loss: 1.3875 Top-1 Acc: 59.5096 Top-5 Acc: 84.5594
3e-4 -> 3e-5 - Epoch 49/50
----------
lr: 3.1313810719888015e-05
train Loss: 1.3785 Top-1 Acc: 59.7117 Top-5 Acc: 85.4507
test Loss: 1.3912 Top-1 Acc: 59.8485 Top-5 Acc: 84.8584
3e-4 -> 3e-5 - Epoch 50/50
----------
lr: 3.0328853214923733e-05
train Loss: 1.3728 Top-1 Acc: 59.8113 Top-5 Acc: 85.6322
test Loss: 1.4018 Top-1 Acc: 59.5594 Top-5 Acc: 84.5195
Training 3e-4 -> 3e-5 complete in 147m 50s
Best test Top-1 Acc: 59.848495
Best test Top-5 Acc: 84.858444
train 3e-4 -> 3e-5 done

3e-4 -> 0 - Epoch 1/50
----------
lr: 5.9999999999999995e-05
train Loss: 3.6553 Top-1 Acc: 3.2438 Top-5 Acc: 12.8923
test Loss: 3.4399 Top-1 Acc: 6.2400 Top-5 Acc: 22.3086
3e-4 -> 0 - Epoch 2/50
----------
lr: 0.00011999999999999999
train Loss: 3.3830 Top-1 Acc: 7.2825 Top-5 Acc: 24.9964
test Loss: 3.2655 Top-1 Acc: 10.0678 Top-5 Acc: 30.3529
3e-4 -> 0 - Epoch 3/50
----------
lr: 0.00017999999999999998
train Loss: 3.2210 Top-1 Acc: 10.6846 Top-5 Acc: 32.1701
test Loss: 3.0505 Top-1 Acc: 13.9354 Top-5 Acc: 37.6894
3e-4 -> 0 - Epoch 4/50
----------
lr: 0.00023999999999999998
train Loss: 3.0687 Top-1 Acc: 13.8676 Top-5 Acc: 37.7259
test Loss: 2.9026 Top-1 Acc: 17.2647 Top-5 Acc: 42.8030
3e-4 -> 0 - Epoch 5/50
----------
lr: 0.0003
train Loss: 2.9301 Top-1 Acc: 17.4084 Top-5 Acc: 42.5592
test Loss: 2.7464 Top-1 Acc: 20.9729 Top-5 Acc: 48.6344
3e-4 -> 0 - Epoch 6/50
----------
lr: 0.0003
train Loss: 2.7798 Top-1 Acc: 20.7034 Top-5 Acc: 47.9682
test Loss: 2.5438 Top-1 Acc: 26.2062 Top-5 Acc: 55.7217
3e-4 -> 0 - Epoch 7/50
----------
lr: 0.0002996346075389736
train Loss: 2.6451 Top-1 Acc: 23.7748 Top-5 Acc: 52.3073
test Loss: 2.4771 Top-1 Acc: 27.7911 Top-5 Acc: 57.4063
3e-4 -> 0 - Epoch 8/50
----------
lr: 0.0002985402103112355
train Loss: 2.5225 Top-1 Acc: 27.0217 Top-5 Acc: 56.1504
test Loss: 2.3075 Top-1 Acc: 32.2269 Top-5 Acc: 62.5299
3e-4 -> 0 - Epoch 9/50
----------
lr: 0.0002967221401100708
train Loss: 2.4120 Top-1 Acc: 29.6993 Top-5 Acc: 59.7857
test Loss: 2.2212 Top-1 Acc: 34.6491 Top-5 Acc: 64.5634
3e-4 -> 0 - Epoch 10/50
----------
lr: 0.00029418925439074776
train Loss: 2.3045 Top-1 Acc: 32.4008 Top-5 Acc: 62.8811
test Loss: 2.1487 Top-1 Acc: 36.1344 Top-5 Acc: 67.3345
3e-4 -> 0 - Epoch 11/50
----------
lr: 0.0002909538931178862
train Loss: 2.2280 Top-1 Acc: 34.5425 Top-5 Acc: 65.0416
test Loss: 2.0522 Top-1 Acc: 38.9753 Top-5 Acc: 69.6272
3e-4 -> 0 - Epoch 12/50
----------
lr: 0.0002870318186463901
train Loss: 2.1483 Top-1 Acc: 36.9941 Top-5 Acc: 67.0953
test Loss: 2.0170 Top-1 Acc: 40.2612 Top-5 Acc: 71.1722
3e-4 -> 0 - Epoch 13/50
----------
lr: 0.000282442138928839
train Loss: 2.0879 Top-1 Acc: 38.4285 Top-5 Acc: 68.9039
test Loss: 1.9346 Top-1 Acc: 42.4143 Top-5 Acc: 73.0463
3e-4 -> 0 - Epoch 14/50
----------
lr: 0.0002772072144234638
train Loss: 2.0309 Top-1 Acc: 40.0024 Top-5 Acc: 70.5342
test Loss: 1.8841 Top-1 Acc: 43.7699 Top-5 Acc: 74.1129
3e-4 -> 0 - Epoch 15/50
----------
lr: 0.00027135254915624206
train Loss: 1.9870 Top-1 Acc: 41.2532 Top-5 Acc: 71.6543
test Loss: 1.8168 Top-1 Acc: 46.3716 Top-5 Acc: 75.8872
3e-4 -> 0 - Epoch 16/50
----------
lr: 0.0002649066664678466
train Loss: 1.9396 Top-1 Acc: 42.4536 Top-5 Acc: 73.0122
test Loss: 1.7943 Top-1 Acc: 46.4314 Top-5 Acc: 76.1264
3e-4 -> 0 - Epoch 17/50
----------
lr: 0.0002579009700507976
train Loss: 1.9014 Top-1 Acc: 43.7540 Top-5 Acc: 73.7616
test Loss: 1.7699 Top-1 Acc: 48.2655 Top-5 Acc: 76.8441
3e-4 -> 0 - Epoch 18/50
----------
lr: 0.00025036959095382864
train Loss: 1.8655 Top-1 Acc: 44.7969 Top-5 Acc: 74.5469
test Loss: 1.7058 Top-1 Acc: 49.3122 Top-5 Acc: 78.0104
3e-4 -> 0 - Epoch 19/50
----------
lr: 0.00024234922129884865
train Loss: 1.8237 Top-1 Acc: 45.9669 Top-5 Acc: 75.7246
test Loss: 1.7508 Top-1 Acc: 48.1659 Top-5 Acc: 78.2297
3e-4 -> 0 - Epoch 20/50
----------
lr: 0.00023387893552061193
train Loss: 1.7992 Top-1 Acc: 46.2452 Top-5 Acc: 76.1784
test Loss: 1.6781 Top-1 Acc: 50.1695 Top-5 Acc: 79.2763
3e-4 -> 0 - Epoch 21/50
----------
lr: 0.0002249999999999999
train Loss: 1.7681 Top-1 Acc: 47.4040 Top-5 Acc: 76.9506
test Loss: 1.6583 Top-1 Acc: 51.5351 Top-5 Acc: 79.3860
3e-4 -> 0 - Epoch 22/50
----------
lr: 0.00021575567201836154
train Loss: 1.7394 Top-1 Acc: 48.4189 Top-5 Acc: 77.5943
test Loss: 1.6619 Top-1 Acc: 50.3389 Top-5 Acc: 79.2265
3e-4 -> 0 - Epoch 23/50
----------
lr: 0.00020619098901238672
train Loss: 1.7141 Top-1 Acc: 49.0787 Top-5 Acc: 78.3449
test Loss: 1.6670 Top-1 Acc: 50.8074 Top-5 Acc: 78.7779
3e-4 -> 0 - Epoch 24/50
----------
lr: 0.00019635254915624205
train Loss: 1.6894 Top-1 Acc: 49.9832 Top-5 Acc: 78.8488
test Loss: 1.5799 Top-1 Acc: 53.3892 Top-5 Acc: 81.0407
3e-4 -> 0 - Epoch 25/50
----------
lr: 0.0001862882843399501
train Loss: 1.6604 Top-1 Acc: 50.8201 Top-5 Acc: 79.5617
test Loss: 1.5954 Top-1 Acc: 52.9705 Top-5 Acc: 81.1204
3e-4 -> 0 - Epoch 26/50
----------
lr: 0.0001760472266500395
train Loss: 1.6344 Top-1 Acc: 51.6291 Top-5 Acc: 80.0740
test Loss: 1.5453 Top-1 Acc: 54.9243 Top-5 Acc: 81.4394
3e-4 -> 0 - Epoch 27/50
----------
lr: 0.00016567926949014795
train Loss: 1.6168 Top-1 Acc: 52.0445 Top-5 Acc: 80.4774
test Loss: 1.5741 Top-1 Acc: 53.4490 Top-5 Acc: 81.7584
3e-4 -> 0 - Epoch 28/50
----------
lr: 0.0001552349245053751
train Loss: 1.5962 Top-1 Acc: 52.8031 Top-5 Acc: 81.0081
test Loss: 1.5568 Top-1 Acc: 54.4258 Top-5 Acc: 81.7484
3e-4 -> 0 - Epoch 29/50
----------
lr: 0.00014476507549462483
train Loss: 1.5748 Top-1 Acc: 53.4137 Top-5 Acc: 81.3415
test Loss: 1.5192 Top-1 Acc: 55.3928 Top-5 Acc: 82.8748
3e-4 -> 0 - Epoch 30/50
----------
lr: 0.00013432073050985194
train Loss: 1.5605 Top-1 Acc: 53.9735 Top-5 Acc: 81.5327
test Loss: 1.4997 Top-1 Acc: 55.9809 Top-5 Acc: 82.8449
3e-4 -> 0 - Epoch 31/50
----------
lr: 0.0001239527733499604
train Loss: 1.5403 Top-1 Acc: 54.6005 Top-5 Acc: 82.0537
test Loss: 1.4938 Top-1 Acc: 56.2301 Top-5 Acc: 83.3832
3e-4 -> 0 - Epoch 32/50
----------
lr: 0.00011371171566004979
train Loss: 1.5221 Top-1 Acc: 55.1303 Top-5 Acc: 82.4300
test Loss: 1.4993 Top-1 Acc: 56.4494 Top-5 Acc: 82.7452
3e-4 -> 0 - Epoch 33/50
----------
lr: 0.00010364745084375787
train Loss: 1.5022 Top-1 Acc: 55.6074 Top-5 Acc: 83.0302
test Loss: 1.4597 Top-1 Acc: 56.9477 Top-5 Acc: 83.8816
3e-4 -> 0 - Epoch 34/50
----------
lr: 9.380901098761316e-05
train Loss: 1.4871 Top-1 Acc: 56.2796 Top-5 Acc: 83.1974
test Loss: 1.4613 Top-1 Acc: 57.2269 Top-5 Acc: 83.8018
3e-4 -> 0 - Epoch 35/50
----------
lr: 8.424432798163834e-05
train Loss: 1.4789 Top-1 Acc: 56.5695 Top-5 Acc: 83.3433
test Loss: 1.4548 Top-1 Acc: 57.6156 Top-5 Acc: 84.3301
3e-4 -> 0 - Epoch 36/50
----------
lr: 7.5e-05
train Loss: 1.4632 Top-1 Acc: 56.9885 Top-5 Acc: 83.6625
test Loss: 1.4338 Top-1 Acc: 58.0044 Top-5 Acc: 84.2005
3e-4 -> 0 - Epoch 37/50
----------
lr: 6.612106447938796e-05
train Loss: 1.4479 Top-1 Acc: 57.5052 Top-5 Acc: 84.1682
test Loss: 1.4256 Top-1 Acc: 58.2636 Top-5 Acc: 84.4597
3e-4 -> 0 - Epoch 38/50
----------
lr: 5.765077870115123e-05
train Loss: 1.4390 Top-1 Acc: 57.9974 Top-5 Acc: 84.0975
test Loss: 1.4331 Top-1 Acc: 58.3732 Top-5 Acc: 84.7488
3e-4 -> 0 - Epoch 39/50
----------
lr: 4.9630409046171234e-05
train Loss: 1.4266 Top-1 Acc: 58.3002 Top-5 Acc: 84.4126
test Loss: 1.4071 Top-1 Acc: 58.8317 Top-5 Acc: 84.7887
3e-4 -> 0 - Epoch 40/50
----------
lr: 4.2099029949202296e-05
train Loss: 1.4184 Top-1 Acc: 58.6356 Top-5 Acc: 84.7633
test Loss: 1.4094 Top-1 Acc: 59.2305 Top-5 Acc: 84.9980
3e-4 -> 0 - Epoch 41/50
----------
lr: 3.5093333532153296e-05
train Loss: 1.4046 Top-1 Acc: 59.0176 Top-5 Acc: 85.1259
test Loss: 1.4026 Top-1 Acc: 58.9912 Top-5 Acc: 85.1774
3e-4 -> 0 - Epoch 42/50
----------
lr: 2.8647450843757884e-05
train Loss: 1.3930 Top-1 Acc: 59.3630 Top-5 Acc: 85.3075
test Loss: 1.4009 Top-1 Acc: 59.2803 Top-5 Acc: 85.2970
3e-4 -> 0 - Epoch 43/50
----------
lr: 2.2792785576536095e-05
train Loss: 1.3879 Top-1 Acc: 59.2986 Top-5 Acc: 85.4099
test Loss: 1.3955 Top-1 Acc: 59.3600 Top-5 Acc: 85.1076
3e-4 -> 0 - Epoch 44/50
----------
lr: 1.7557861071160976e-05
train Loss: 1.3813 Top-1 Acc: 59.6613 Top-5 Acc: 85.3355
test Loss: 1.3972 Top-1 Acc: 59.5993 Top-5 Acc: 85.3967
3e-4 -> 0 - Epoch 45/50
----------
lr: 1.2968181353609881e-05
train Loss: 1.3792 Top-1 Acc: 59.8349 Top-5 Acc: 85.4855
test Loss: 1.3878 Top-1 Acc: 59.6292 Top-5 Acc: 85.3867
3e-4 -> 0 - Epoch 46/50
----------
lr: 9.046106882113748e-06
train Loss: 1.3695 Top-1 Acc: 60.3191 Top-5 Acc: 85.5550
test Loss: 1.3887 Top-1 Acc: 60.0179 Top-5 Acc: 85.5463
3e-4 -> 0 - Epoch 47/50
----------
lr: 5.810745609252196e-06
train Loss: 1.3633 Top-1 Acc: 60.3487 Top-5 Acc: 85.8621
test Loss: 1.3843 Top-1 Acc: 59.9681 Top-5 Acc: 85.5163
3e-4 -> 0 - Epoch 48/50
----------
lr: 3.2778598899291452e-06
train Loss: 1.3612 Top-1 Acc: 60.1971 Top-5 Acc: 85.9133
test Loss: 1.3810 Top-1 Acc: 59.6890 Top-5 Acc: 85.5662
3e-4 -> 0 - Epoch 49/50
----------
lr: 1.4597896887644617e-06
train Loss: 1.3677 Top-1 Acc: 60.2171 Top-5 Acc: 85.7329
test Loss: 1.3837 Top-1 Acc: 59.9382 Top-5 Acc: 85.5961
3e-4 -> 0 - Epoch 50/50
----------
lr: 3.653924610263702e-07
train Loss: 1.3585 Top-1 Acc: 60.5626 Top-5 Acc: 85.9097
test Loss: 1.3826 Top-1 Acc: 59.9681 Top-5 Acc: 85.6360
Training 3e-4 -> 0 complete in 147m 52s
Best test Top-1 Acc: 60.017948
Best test Top-5 Acc: 85.635956
train 3e-4 -> 0 done