AlexNet

发表于 2019-06-08 更新于 2021-07-09 分类于目标分类/object classification 阅读次数：

本文字数： 4k 阅读时长 ≈ 7 分钟

AlexNet在ImageNet LSVRC-2010的1000类分类比赛上实现了37.5% top-1和17.0% top-5的最小误差率，在LSVRC-2012上实现了15.3% top-5的最小误差率，这些数据是当时最好的识别结果，其实现代码也在google code上公开：cuda-convnet

本文学习AlexNet网络结构及其训练方法

预处理

AlexNet除了减去均值以外，没有执行任何预处理操作

网络架构

首先介绍最初的双GPU AlexNet架构，再介绍单GPU的AlexNet架构

双GPU AlexNet

在文章ImageNet Classification with Deep Convolutional Neural Networks中，AlexNet使用双GPU进行训练，其结构如下所示：

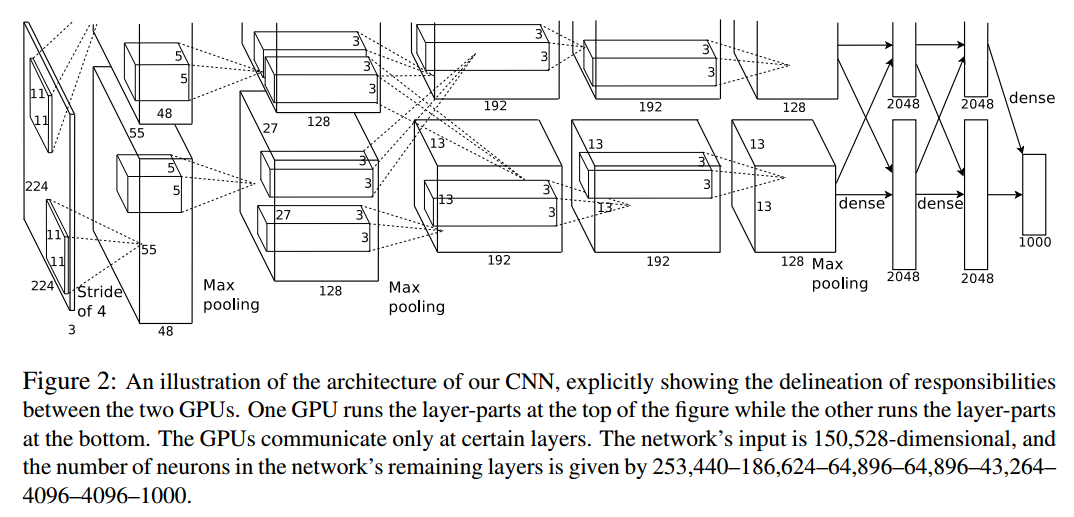
AlexNet包含8个可学习层：5个卷积层 + 3个全连接层组成

第二/四/五个卷积层的核仅与同一GPU的前一层进行连接
第三个卷积层的核与第二层全部连接
全连接层的核与前一层全部连接
局部归一化层跟随在第一二个卷积层后
重叠池化层跟随在局部归一化层后以及第5个卷积层后
第三、第四和第五个卷积层直接连接
卷积层和全连接层都使用ReLU作为激活函数

单GPU AlexNet

单GPU训练的AlexNet模型如下（已去除LRN）：

	输入大小	滤波器大小	步长	零填充	滤波器个数	输出大小
CONV1	227x227x3	11x11x3	4	0	96	55x55x96
POOL2	55x55x96	3x3	2	/	96	27x27x96
CONV3	27x27x96	5x5x96	1	2	256	27x27x256
POOL4	27x27x256	3x3	2	/	256	13x13x256
CONV5	13x13x256	3x3x256	1	1	384	13x13x384
CONV6	13x13x384	3x3x384	1	1	384	13x13x384
CONV7	13x13x384	3x3x384	1	1	256	13x13x256
POOL8	13x13x256	3x3	2	/	256	6x6x256
FC9	1x1x9216	1x1	/	/	4096	1x1x4096
FC10	1x1x4096	1x1	/	/	4096	1x1x4096
FC11	1x1x4096	1x1	/	/	1000	1x1x1000

`224`还是`227`

在原文中作者输入图像大小为224x224，不过经过推算不符合网络计算，应该使用227x227作为输入图像大小

神经元和参数个数

整个网络约有6千万个参数和65万个神经元，计算如下：

输入层大小227x227x3，输入维数是15,4587
第一层卷积层卷积核大小为11x11x3，步长4，滤波器个数96，所以参数个数是(11x11x3)x96+96=3,4944，输出大小为55x55x96=29,0400
- 池化层滤波器大小为3x3，步长2，所以输出大小为27x27x96
第二层卷积层卷积核大小为5x5x96，零填充2，滤波器个数256，所以参数个数是(5x5x96)x256+256=61,4656，输出大小为27x27x256=18,6624
- 池化层滤波器大小为3x3，步长2，所以输出大小为13x13x256
第三层卷积层卷积核大小为3x3x256，零填充1，滤波器个数是384个，所以参数个数是(3x3x256)x384+384=88,5120，输出大小为13x13x384=6,4896
第四层卷积层卷积核大小为3x3x384，零填充1，滤波器个数是384个，所以参数个数是(3x3x384)x384+384=132,7488，输出大小为13x13x384=6,4896
第五层卷积层卷积核大小为3x3x384，零填充1，滤波器个数是256，所以参数个数是(3x3x384)x256+256=88,4992，输出大小为13x13x256=4,3264
- 池化层滤波器大小为3x3，步长2，所以输出大小为6x6x256
第一层全连接层大小为4096，所以参数个数是(6x6x256)x4096+4096=3775,2832，输出大小为4096
第二层全连接层大小为4096，所以参数个数是4096x4096+4096=1678,1312，输出大小为4096
输出层大小为1000，所以参数个数是4096x1000+1000=409,7000

神经元总个数是15,4587+29,0400+18,6624+6,4896+6,4896+4,3264+4096+4096+1000=81,3859（不包括输入层就是65,9272）

参数总个数是3,4944+61,4656+88,5120+132,7488+88,4992+3775,2832+1678,1312+409,7000=6237,8344

特性

主要有4点：

使用ReLU作为激活函数提高训练速度
多GPU训练
使用局部响应归一化(LRN)方法增加泛化能力
使用重叠池化层（Overlapping Pool）提高泛化能力

ReLU

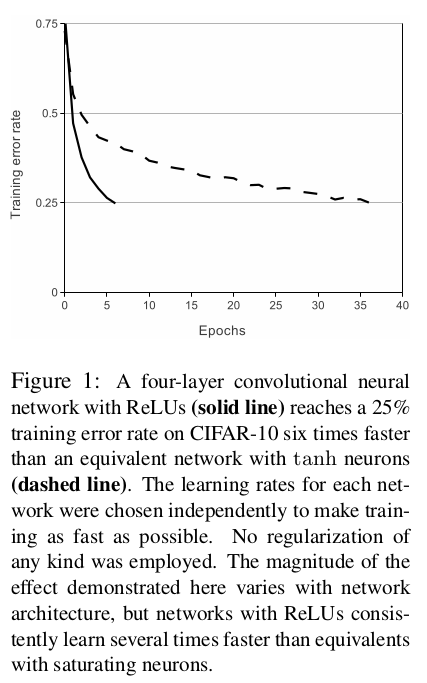
之前标准的激活函数是tanh()和sigmoid()函数，文章中使用ReLU(Rectified Linear Units，修正线性单元)作为神经元激活函数

使用4层卷积神经网络训练CIFAR-10数据集，比较达到25%训练误差率的时间，使用ReLU能够比tanh快6倍

多GPU训练

AlexNet使用两块GTX 580 GPU，在深度上进行切分，将每层一半神经元分别放置在不同GPU上进行训练

局部响应归一化

数学实现如下：

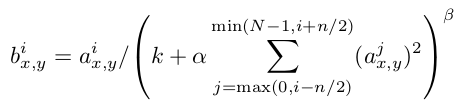
经过ReLU激活后的卷积图，第i层上的位置为(x,y)的神经元值a，需要除以其相邻n个层相同位置的神经元值之和。常量k，n，\(\alpha\)，\(\beta\)都是超参数，需要通过验证集设定，当前设定为\(k=2，n=5，\alpha=10^{-4}，beta=0.75\)

其目的是实现神经元的侧抑制（lateral inhibition），在不同层之间进行竞争，使响应值大的神经元变得更大，并抑制其他较小的神经元

LRN（Local Response Normalization，局部响应归一化）能够提高泛化能力：在ImageNet 1000类分类任务中，LRN减少了1.4% top-1和1.2% top5的错误率；在cifar-10数据集测试中，一个4层神经网络能达到13%测试误差率（没有LRN）和11%测试误差率（有LRN）

在之后其他网络的测试中发现LRN对训练结果提高几乎没有影响，所以不再使用

重叠池化层

传统的池化层步长和滤波器大小相同（s=z=2），所以滤波器操作不会重叠

alexnet使用重叠池化（Overlapping Pool）操作，步长小于滤波器大小（s=2,x=3,s<z），这在1000类分类任务上能够实现0.4% top-1和0.3% top-5的提高。在训练过程中能够发现重叠池化模型更难以过拟合

避免过拟合手段

数据扩充（data augmentation）
随机失活（dropout）

数据扩充

文章中提到了两种方式

第一种方式是生成图像转换和水平映射。在训练阶段，获取256x256大小的数据集，再从中随机获取227x227大小的训练图像，同时通过水平映像(horizontal reflection)操作来扩大数据集；在测试阶段，使用同样方式裁剪5个\(227\times 227\)大小图像，并进行水平翻转，平均这10个图像预测结果作为输出

第二种方式是改变训练数据的通道强度，对于每个RGB图像像素\(I_{xy}=[I_{xy}^{B},I_{xy}^{G},I_{xy}^{B}]^{T}\)，添加如下值：

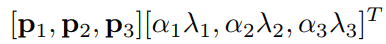
其中\(p_{i}\)是第i个特征向量（eigenvector），\(\lambda_{i}\)是RGB像素值3x3协方差矩阵（covariance matrix）的特征值，\(\alpha_{i}\)是符合零均值(mean zero)和0.1标准方差(standard deviation)的服从高斯分布的随机变量，特定训练图像上的每个像素使用的\(\alpha_{i}\)都不相同，再次训练时需要重新设置\(\alpha_{i}\)

使用PCA改变图像强度的理论基础是自然图像的一个重要特性：物体同一性不随照明强度和颜色的变化而变化

这种方法减少了至少1% top-1误差率

随机失活

集合不同网络模型进行预测能够很好的减少测试误差，但是对于大网络而言需要耗费很多时间进行训练。随机失活（dropout）操作对中间隐含层进行操作，以0.5的概率判断该神经元是否失效，即这个神经元不进行前向操作，也不进行反向更新

有两点优势：

每次进行训练都是在不同的网络架构上，与此同时这些不同的网络架构共享同一套权重
减少神经元复杂的共适应性（co-adaptation），神经元不能依赖于某个特定的神经元

在测试阶段，对所有神经元的输出都乘以0.5，以获取指数多个dropout网络产生的预测分布的几何平均值

在alexnet模型中，对前两个全连接层进行dropout操作。如果没有dropout，整个网络会严重过拟合，并且训练过程达到收敛的时间大致增加了一倍

学习细节

批量大小为128，使用动量值为0.9，权重衰减率为5e-4，权重更新公式如下：

\[ v_{i+1} = 0.9\cdot v_{i} - 0.0005\cdot lr\cdot w_{i} - lr \triangledown w_{i}\\ w_{i+1} = w_{i} + v_{i+1} \]

权重初始化为0均值，0.01标准差的高斯分布

第二、第四、第五个卷积层层和全连接层的偏置值初始化为\(1\)，其他层的偏置值初始化为\(0\)

学习率初始化为0.01，在终止之前共减少了3次

大海

AlexNet

预处理