权重初始化

发表于 更新于 分类于
本文字数： 3.2k 阅读时长 ≈ 6 分钟

合理的权重初始化操作有助于实现更快的训练和得到更好的结果，cs231n中讨论了不同的初始化权重方式：Weight Initialization

全零初始化

有一个合理性假设是保持初始化后的权重值一半为正一半为负，即权重均值为零。虽然直接设置权重为零符合这一假设，但因为全零权重导致神经元输出一致，在反向传播中计算得到相同梯度并进行同样的权重更新，无法训练得到好的模型

这也给出一个方向在于初始化后的权重虽然基于均值为零的前提，但应该打破正负两边的对称性

小随机数初始化

通常用小随机数赋值权重，同时保证对称打破（symmetry breaking），实现如下：

1
W = 0.01 * np.random.randn(D, H)

这样得到的权重符合均值为零，方差为0.01的正态分布

注意：不一定是权重越小越好，因为计算得到的梯度跟权重值呈正相关，对于深度网络而言，梯度在反向传播过程中会随着层的递增而越来越小，出现梯度弥散现象

方差校准

使用小随机数初始化方式得到的权重会导致神经元输出分布的方差会随着输入神经元个数的增长而增长。推导如下，假设点积操作为\(s = \sum_{i}^{n} w_{i}x_{i}\)，输出结果\(s\)的方差计算如下：

\[ Var(s) = Var(\sum_{i}^{n}w_{i}x_{i})=\sum_{i}^{n}Var(w_{i}x_{i})\\ =\sum_{i}^{n}([E(w_{i})]^{2}Var(x_{i}) + [E(x_{i})]^{2}Var(w_{i})) + Var(x_{i})Var(w_{i})\\ =\sum_{i}^{n}Var(x_{i})Var(w_{i}) =nVar(w)Var(x) =Var(\frac {1}{n}w)Var(x) \]

上述推导基于如下定义，参考：Product of independent variables

\[ Var(XY) = [E(X)]^{2}Var(Y) + [E(Y)]^{2}Var(X) + Var(X)Var(Y)\\ Var(aX) = a^{2}Var(X) \]

基于输入数据和权重的均值为零：\(E(w)=0\)、\(E(x)=0\)

为保持输入输出具有同样分布，所以需要对权重除以\(\frac {1}{\sqrt n}\)。修改权重初始化方式：

1
W = weight_scale * np.random.rand(n) / sqrt(n)

其中\(n\)是每层输入神经元的个数

文章Understanding the difficulty of training deep feedforward neural networks基于对反向传播梯度的折衷和等效分析（compromise and an equivalent analysis），提出的权重分布为\(Var(w) = 2/(n_{in}+n_{out})\)，其中\(n_{in}\)和\(n_{out}\)是上一层和下一层的神经元数量，初始化方式如下：

1
W = weight_scale * np.random.randn(n) * 2 / (n_in + n_out)

文章Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification是最新的一个研究，其初始化方式为

1
W = weight_scale * np.random.randn(n) * sqrt(2.0/n)

是目前推荐的使用ReLU的网络的权重初始化方法

另一种解决方差校正的方式是使用稀疏初始化

偏置值校正

打破对称影响以通过权重初始化实现，简单设置偏置向量为0即可

测试

选择小随机数初始化方式以及2种方差校正方式进行测试

参考：weight_initialize.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
import numpy as np


def weight_initialize_v1(D, H, weight_scale=1e-2):
    """
    小随机数初始化权重
    :return:
    """
    return weight_scale * np.random.randn(D, H)


def weight_initialize_v2(D, H, weight_scale=1e-2):
    """
    方差校正方式一
    :return:
    """
    return weight_scale * np.random.randn(D, H) / np.sqrt(D)


def weight_initialize_v3(D, H, weight_scale=1e-2):
    """
    方差校正方式二
    :return:
    """
    return weight_scale * np.random.randn(D, H) * np.sqrt(2.0 / D)
  • 数据集设置：使用CIFAR10数据集，从中取5000张作为小测试集进行训练
  • 超参数设置：初始学习率1e-3，迭代100轮，批量大小为200
  • 使用Adam实现权重更新
  • 使用3层网络，大小为32*32*3 -> 400 -> 200 -> 10

完整实现参考：weight_initialize.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
# -*- coding: utf-8 -*-

# @Time    : 19-8-3 下午8:51
# @Author  : zj

from datas.cifar import get_CIFAR10_data
from classifier.nn_classifier import NN
import matplotlib.pyplot as plt

cifar_path = '/home/zj/data/cifar-10-batches-py'


def plot(results):
    for k, v in results.items():
        plt.plot(v, label=k)
    plt.legend()
    plt.show()


if __name__ == '__main__':
    data_dict = get_CIFAR10_data(cifar_path, val_size=0.1)

    x_val = data_dict['X_val']
    y_val = data_dict['y_val']

    x_val_flatten = x_val.reshape(x_val.shape[0], -1)

    D = 32 * 32 * 3
    H1 = 400
    H2 = 200
    O = 10

    weight_init_list = ['v1', 'v2', 'v3']
    loss_dict = {}
    for item in weight_init_list:
        classifier = NN([H1, H2], input_dim=D, num_classes=O, learning_rate=1e-3, weight_init=item)
        loss_history = classifier.train(x_val_flatten, y_val, num_iters=50, verbose=True)
        loss_dict[item] = loss_history
    plot(loss_dict)

训练100轮后的损失值变化如下：

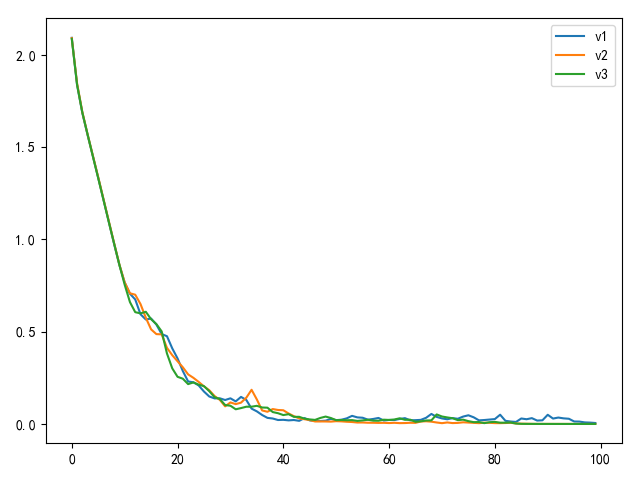
从上图可知，使用小随机数初始化以及方差矫正方法的结果类似，不过使用推荐方式进行初始化的权重收敛曲线更平稳

小结

对于使用ReLU的网络，权重和偏置向量初始化方式如下：

1
2
W = weight_scale * np.random.randn(D, H) * sqrt(2.0/D)
b = np.zeros((1, H))