Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression
原文地址:Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression
官方实现:generalized-iou
摘要
Intersection over Union (IoU) is the most popular evaluation metric used in the object detection benchmarks. However, there is a gap between optimizing the commonly used distance losses for regressing the parameters of a bounding box and maximizing this metric value. The optimal objective for a metric is the metric itself. In the case of axis-aligned 2D bounding boxes, it can be shown that IoU can be directly used as a regression loss. However, IoU has a plateau making it infeasible to optimize in the case of non-overlapping bounding boxes. In this paper, we address the weaknesses of IoU by introducing a generalized version as both a new loss and a new metric. By incorporating this generalized IoU (GIoU) as a loss into the state-of-the art object detection frameworks, we show a consistent improvement on their performance using both the standard, IoU based, and new, GIoU based, performance measures on popular object detection benchmarks such as PASCAL VOC and MS COCO.
交并比(Intersection over Union,IoU)是目标检测领域中使用最为广泛的评估指标。为了最大化IoU,通常会使用距离损失来训练目标框。实际上针对某一指标的最优目标函数即是该指标本身,所以可以直接使用IoU作为回归损失,但是IoU存在一个缺陷,即在预测框和标注框没有重叠的情况下难以优化。本文针对IoU的这一缺陷设计了一个泛化版本,它既作为一种新的损失函数,也作为一种新的度量标准。我们将这个泛化IoU(Generalized IoU,GIoU)作为损失函数集成到目前最先进的目标检测框架中,在PASCAL VOC和MS COCO等流行的目标检测基准数据集上显示,无论采用基于标准IoU的评估方式还是新的基于GIoU的度量方式,算法性能都得到了持续且一致的提升。
IoU
IoU,也称为雅可比索引(Jaccard index),是最常用的计算两个任意形状之间相似度的度量标准。IoU在计算过程中将两个边界框的形状属性(shape property,宽度、高度和位置)编码为区域属性(region property,也就是基于边界框的面积),最后得到一个归一化指标,这使得IoU对于不同大小的边界框具有尺度不变性(因为比较的是面积)。
Intersection over Union (IoU)计算公式如下:
\[ IoU=\frac{\left| A\cap B \right|}{\left| A\cup B \right|} \]
- \(A\)和\(B\)分别代表预测边界框和真实边界框所覆盖的区域;
- \(A\cap B\)表示\(A\)和\(B\)的交集,即两个边界框重叠的区域;
- \(A\cup B\)表示\(A\)和\(B\)的并集,即两个边界框覆盖的总面积,包括它们重叠的部分和各自独有的部分。
公式中的分子\(\left| A\cap B \right|\)计算的是两个边界框重叠区域的面积,而分母\(\left| A\cup B \right|\)则是两个边界框覆盖的总面积。IoU 的值介于 0 和 1 之间,其中:
- 如果\(IoU=1\),意味着\(A\)和\(B\)完全重叠,即预测框与真实框完全吻合;
- 如果\(IoU=0\),意味着\(A\)和\(B\)没有任何重叠,即预测框与真实框没有任何区域相交。
在目标检测算法的训练流程中,优化边界框定位的传统策略常依赖于\(l_{n}\)范数损失函数,旨在通过缩减真实标注框与模型预测框之间的差距,间接提升交并比(IoU)的评价指标。然而,此类损失函数在面对特定场景时暴露出其局限性,未能精准反映不同尺寸与位置的边界框间的真实差异。如下图1所示,绿色框表示标注框,黑色框表示预测框。虽然这些情况下的标注框和预测框拥有不同的IoU值,但是它们的L2损失值或者L1损失值是相同大小的,说明单纯依靠范数损失函数可能无法全面捕捉边界框匹配的细微差异,特别是在涉及框大小与位置偏移的复杂场景中,其评估效果欠佳,进而限制了模型优化的精度与效率。
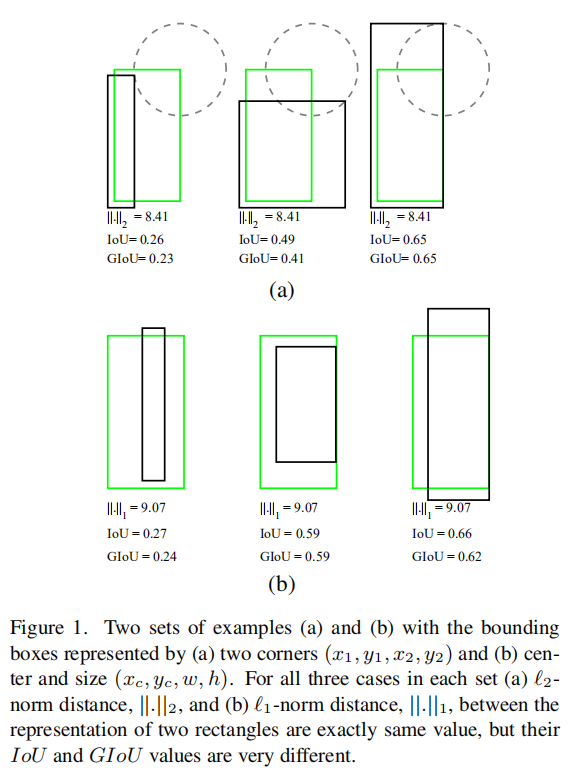
论文首先尝试直接使用IoU作为损失函数,但是发现它存在缺陷,就是对于两个不重叠的标注框和预测框,IoU值等于0,那么训练过程中它的梯度值也是0,也就无法进行训练优化。论文提出一种新的度量标注:GIoU,它是IoU的泛化版本。首先它参考了IoU定义,将形状属性编码为区域属性来计算面积,这样可以保证GIoU拥有尺度不变属性。其次,它确保了标注框和预测框在不重叠的情况下依旧具有强相关性。
GIoU

基于IoU的损失函数的计算公式是\(L_{IoU}=1-IoU\),当\(\left| A\cap B \right|=0\)的时候,\(IoU(A,B)=0\),这种情况下,IoU无法反映两个边界框的相互关系。论文提出的GIoU(Generalized Intersection over Union)解决了这个问题:
\[ GIoU=IoU - \frac{\left| C \setminus (A\cup B) \right|}{\left| C \right|} \]
- \(C\)表示包含特定几何形状的\(A\)和\(B\)的最小凸边型(the smallest convex shapes)。如果\(A\)和\(B\)都是矩形,那么\(C\)就是\(A\)和\(B\)的最小外接矩形(Minimum Bounding Rectangle);
- \(\left| C \setminus (A\cup B) \right|\)表示\(C\)减去\(A\)和\(B\)的并集,\(\frac{\left| C \setminus (A\cup B) \right|}{\left| C \right|}\)得到的是排除\(A\)和\(B\)区域的\(C\)中其他区域的面积占比。
GIoU的取值范围是[−1,1],
- 当预测框和真实框完全重合时,GIoU 的值为1;
- 当预测框和真实框没有重叠,并且随着它们之间的距离增加,GIoU的值会从0逐渐减小到-1。而且在空间上远离到最大程度时,GIoU的值为-1。
GIoU Loss是基于GIoU的损失函数,使用GIoU作为距离函数,其计算公式如下:\(L_{GIoU}=1-GIoU\),它的取值范围是[0,2]。
- 当GIoU=1时,1-GIoU=0,这是损失函数的最低点,表示预测和真实框完美匹配;
- 当GIoU在(-1,1)范围内变化时,1-GIoU在(0, 2)范围内变化;
- 理论上当GIoU=-1时,1-GIoU=2,这是损失函数的最大值,表示预测框和真实框的匹配度极差。

实验
在论文贴出的实验结果来看,比较不同的目标检测算法(Faster-RCNN/Mask-RCNN/YOLOv3)、不同的坐标损失函数(MSELoss/L1-smooth/IoULoss/GIoULoss)、不同的评估标准(IoU/GIoU)和不同数据集(PASCAL VOC 2007/COCO),GIoU作为损失函数均能够提升算法性能。
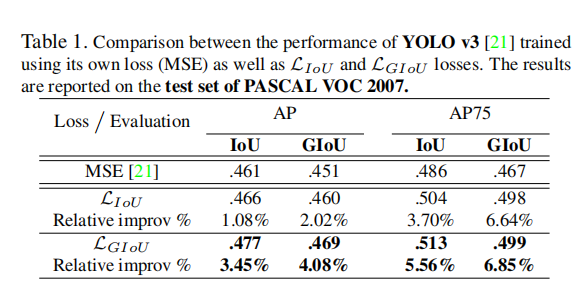
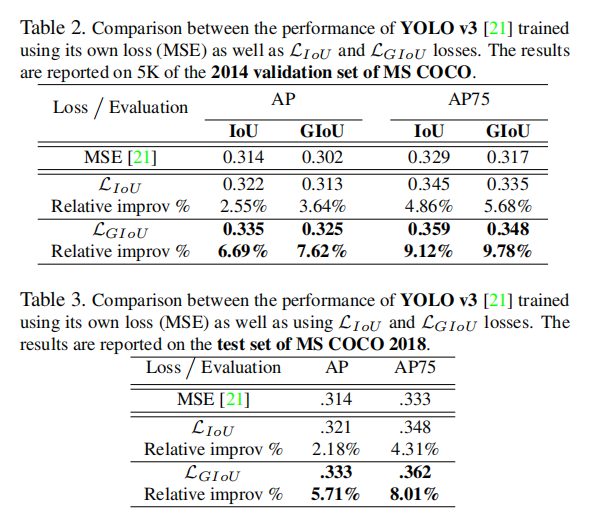
小结
论文有两点创新:
- 提出新的训练思路:优化度量标准的最佳目标函数是度量标准本身(The optimal objective for a metric is the metric itself.);
- 提出新的损失函数:GIoU损失函数,改进IoU损失函数无法有效计算不重叠情况下预测框和标注框的损失。
另外,我尝试着将GIoU Loss作为box_loss加入YOLOv3损失函数,保持原先训练配置情况下发现训练过程中box_loss很难收敛。相信会有其他人也想到采用iou_loss方式来优化目标检测算法,但是如何解决不重叠框的损失计算,如何在实际训练中真正的提高算法性能,是GIoU成立的关键。