1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
|
import torch
import numpy as np
from sklearn import utils
import pandas as pd
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
data_path = '../data/iris-species/Iris.csv'
def load_data(shuffle=True, tsize=0.8):
"""
加载iris数据
"""
data = pd.read_csv(data_path, header=0, delimiter=',')
if shuffle:
data = utils.shuffle(data)
pd_indicator = pd.get_dummies(data['Species'])
indicator = np.array(
[pd_indicator['Iris-setosa'], pd_indicator['Iris-versicolor'], pd_indicator['Iris-virginica']]).T
species_dict = {
'Iris-setosa': 0,
'Iris-versicolor': 1,
'Iris-virginica': 2
}
data['Species'] = data['Species'].map(species_dict)
data_x = np.array(
[data['SepalLengthCm'], data['SepalWidthCm'], data['PetalLengthCm'], data['PetalWidthCm']]).T
data_y = data['Species']
x_train, x_test, y_train, y_test = train_test_split(data_x, data_y, train_size=tsize, test_size=(1 - tsize),
shuffle=False)
y_train = np.atleast_2d(y_train).T
y_test = np.atleast_2d(y_test).T
y_train_indicator = np.atleast_2d(indicator[:y_train.shape[0]])
return torch.from_numpy(x_train).float(), torch.from_numpy(x_test).float(), torch.from_numpy(
y_train), torch.from_numpy(y_test), torch.from_numpy(y_train_indicator).float()
def linear(x, w):
"""
线性操作
:param x: 大小为(m,n+1)
:param w: 大小为(n+1,k)
:return: 大小为(m,k)
"""
return x.mm(w)
def softmax(x):
"""
softmax归一化计算
:param x: 大小为(m, k)
:return: 大小为(m, k)
"""
x -= torch.unsqueeze(torch.max(x, 1)[0], 1)
exps = torch.exp(x)
return exps / torch.unsqueeze(torch.sum(exps, dim=1), 1)
def compute_scores(X, W):
"""
计算精度
:param X: 大小为(m,n)
:param W: 大小为(k,n)
:return: (m,k)
"""
return softmax(linear(X, W))
def compute_loss(scores, indicator, W, la=2e-4):
"""
计算损失值
:param scores: 大小为(m, k)
:param indicator: 大小为(m, k)
:param W: (n+1, k)
:return: (1)
"""
loss = -1 / scores.size()[0] * torch.sum(torch.log(scores) * indicator)
reg = la / 2 * torch.sum(W ** 2)
return (loss + reg).item()
def compute_gradient(indicator, scores, x, W, la=2e-4):
"""
计算梯度
:param indicator: 大小为(m,k)
:param scores: 大小为(m,k)
:param x: 大小为(m,n+1)
:param W: (n+1, k)
:return: (n+1,k)
"""
dloss = -1 / scores.size()[0] * x.t().mm(torch.sub(indicator, scores))
dreg = la * W
return dloss + dreg
def compute_accuracy(scores, Y):
"""
计算精度
:param scores: (m,k)
:param Y: (m,1)
"""
predictions = torch.argmax(scores, dim=1)
res = (predictions == Y.squeeze())
return 1.0 * torch.sum(res).item() / scores.size()[0]
def draw(res_list, title=None, xlabel=None):
if title is not None:
plt.title(title)
if xlabel is not None:
plt.xlabel(xlabel)
plt.plot(res_list)
plt.show()
def compute_gradient_descent(batch_size=8, epoches=2000, alpha=2e-4):
x_train, x_test, y_train, y_test, y_train_indicator = load_data()
m, n = x_train.size()[:2]
k = 3
W = 0.01 * torch.randn(n + 1, k, requires_grad=False, dtype=torch.float)
x_train = torch.from_numpy(np.insert(x_train.numpy(), 0, np.ones(m), axis=1))
x_test = torch.from_numpy(np.insert(x_test.numpy(), 0, np.ones(x_test.size()[0]), axis=1))
loss_list = []
accuracy_list = []
bestW = None
bestA = 0
range_list = list(range(0, m - batch_size, batch_size))
for i in range(epoches):
for j in range_list:
data = x_train[j:j + batch_size]
labels = y_train_indicator[j:j + batch_size]
scores = compute_scores(data, W)
tempW = W - alpha * compute_gradient(labels, scores, data, W)
W = tempW
if j == range_list[-1]:
loss = compute_loss(scores, labels, W)
loss_list.append(loss)
accuracy = compute_accuracy(compute_scores(x_train, W), y_train)
accuracy_list.append(accuracy)
if accuracy >= bestA:
bestA = accuracy
bestW = W.clone()
break
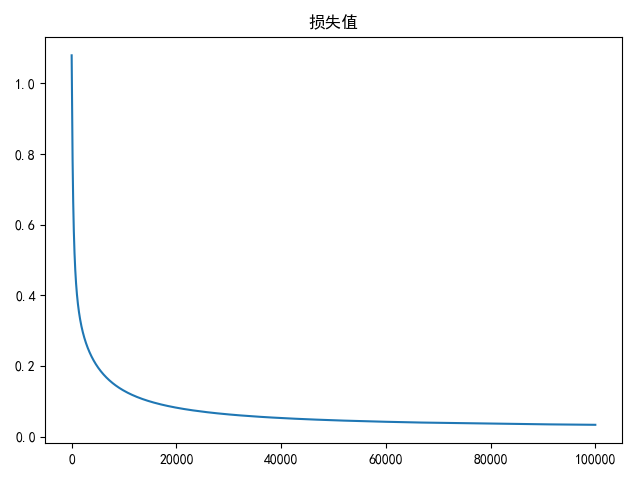
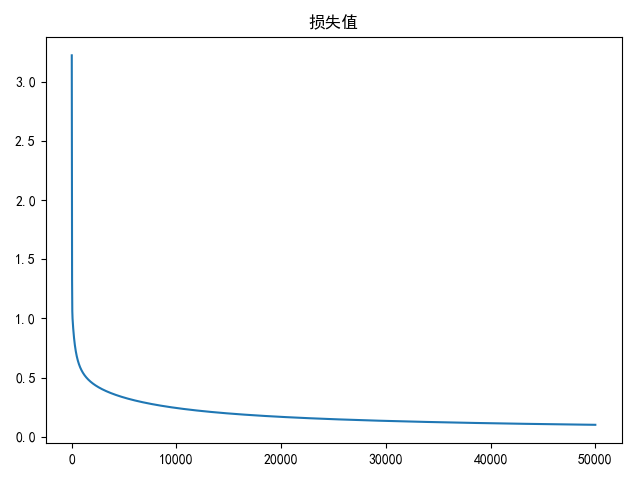
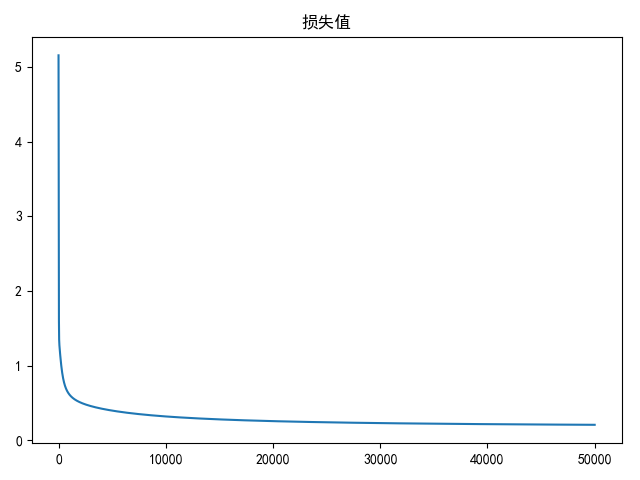
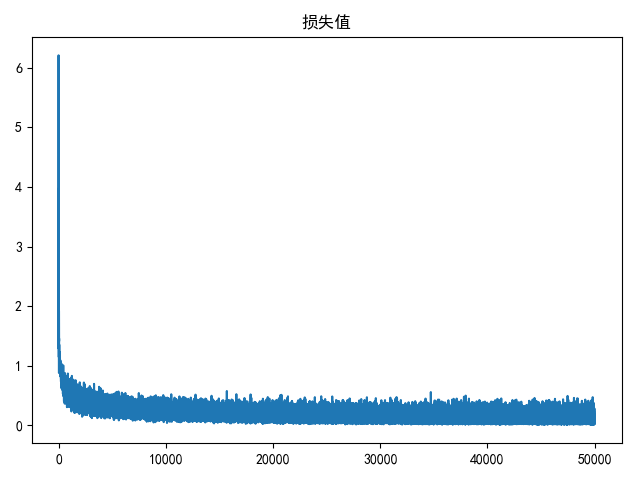
draw(loss_list, title='损失值')
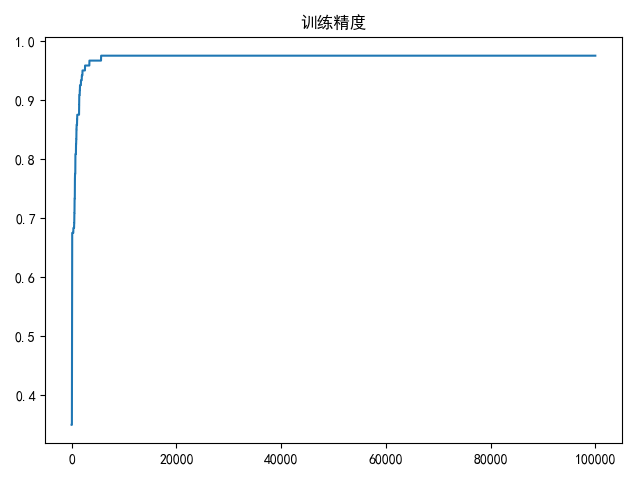
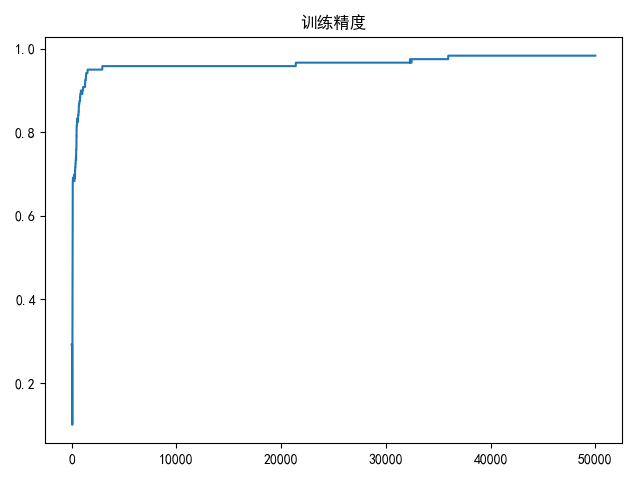
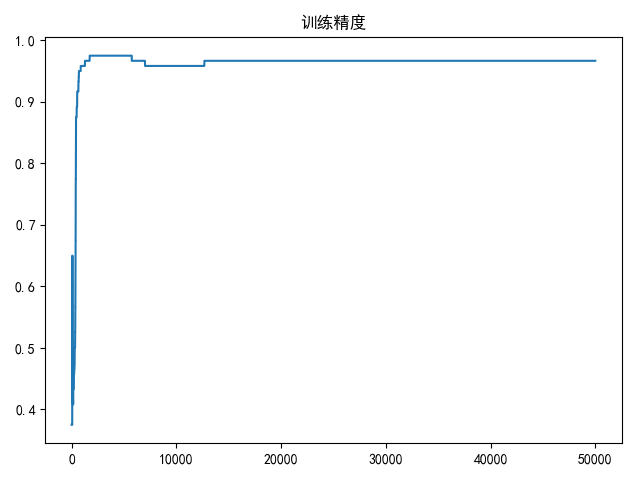
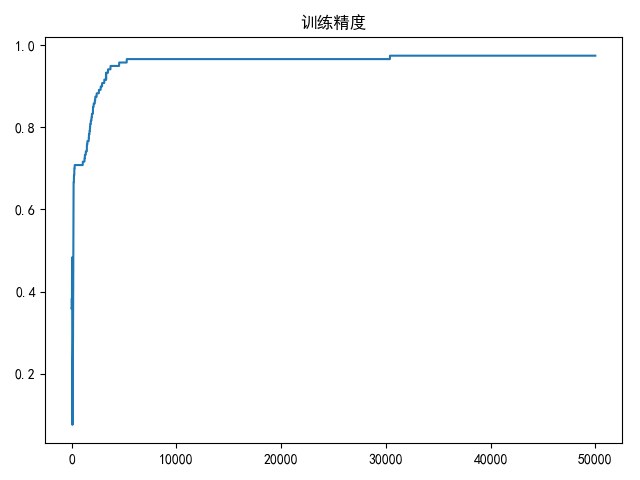
draw(accuracy_list, title='训练精度')
print(bestA)
print(compute_accuracy(compute_scores(x_test, bestW), y_test))
if __name__ == '__main__':
compute_gradient_descent(batch_size=8, epoches=100000)
|
未找到相关的 Issues 进行评论
请联系 @zjykzj 初始化创建