ACNet
论文地址:ACNet: Strengthening the Kernel Skeletons for Powerful CNN via Asymmetric Convolution Blocks
官方实现:DingXiaoH/ACNet
自定义实现:ZJCV/ZCls
摘要
1 | As designing appropriate Convolutional Neural Network (CNN) architecture in the context of a given |
在给定应用场景的情况下去设计合适的卷积神经网络通常包含了繁重的人工工作以及大量的GPU时间,当前研究社区正在寻求架构中立的CNN结构,这些结构可以很容易地插入到多个成熟的架构中,以提高实际应用的性能。我们提出了非对称卷积块(ACB),一个架构中性的结构作为CNN构造块,它使用1D非对称卷积来加强平方卷积核。对于现有架构而言,我们用ACB代替标准的平方核卷积层来构建非对称卷积网络(ACNet),它可以被训练以达到更高的精度水平。经过训练后,我们等效地将ACNet转换成相同的原始架构,因此不再需要额外的计算。我们观察到ACNet可以显著提高CIFAR和ImageNet上各种模型的性能。通过进一步的实验,我们将ACB算法的有效性归因于它能够增强模型对旋转失真的鲁棒性和增强方形卷积核的中心骨架部分。
解读
ACNet的核心在于提出了一个构建块 - 非对称卷积块(Asymmtric Convolution Block, ACB)。在训练阶段,将ACB替代标准卷积进行训练;在测试阶段,将ACB还原回标准卷积。通过分离训练阶段和测试阶段的模型,在训练时提高了算法泛化能力,在测试时保留了原始模型的执行速度
公式推理
卷积层操作
第
其中2D卷积操作,
批量归一化层操作
批量归一化操作通常位于卷积层之后,其计算公式如下:
卷积可加性
1 | if several 2D kernels with compatible sizes operate on the same input with the same stride to produce outputs of the same resolution, and their outputs are summed up, we can add up these kernels on the corresponding positions to obtain an equivalent kernel which will produce the same output |
简单地说,如果多个卷积滤波器能够对同一输入计算得到相同大小输出,那么这些滤波器的卷积核可以相加在一起,其计算得到的输出和分开计算的输出求和后的结果相同。计算公式如下所示
2D卷积核
注意一:不同卷积核需要兼容。满足如下等式即可
注意二:输入矩阵
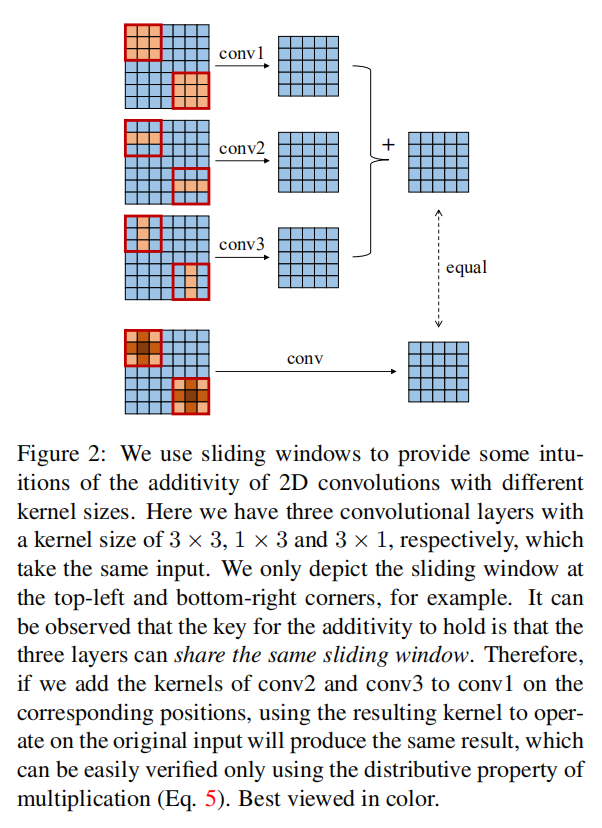
- 对于大小为
- 同理,对于大小为
ACB
训练阶段
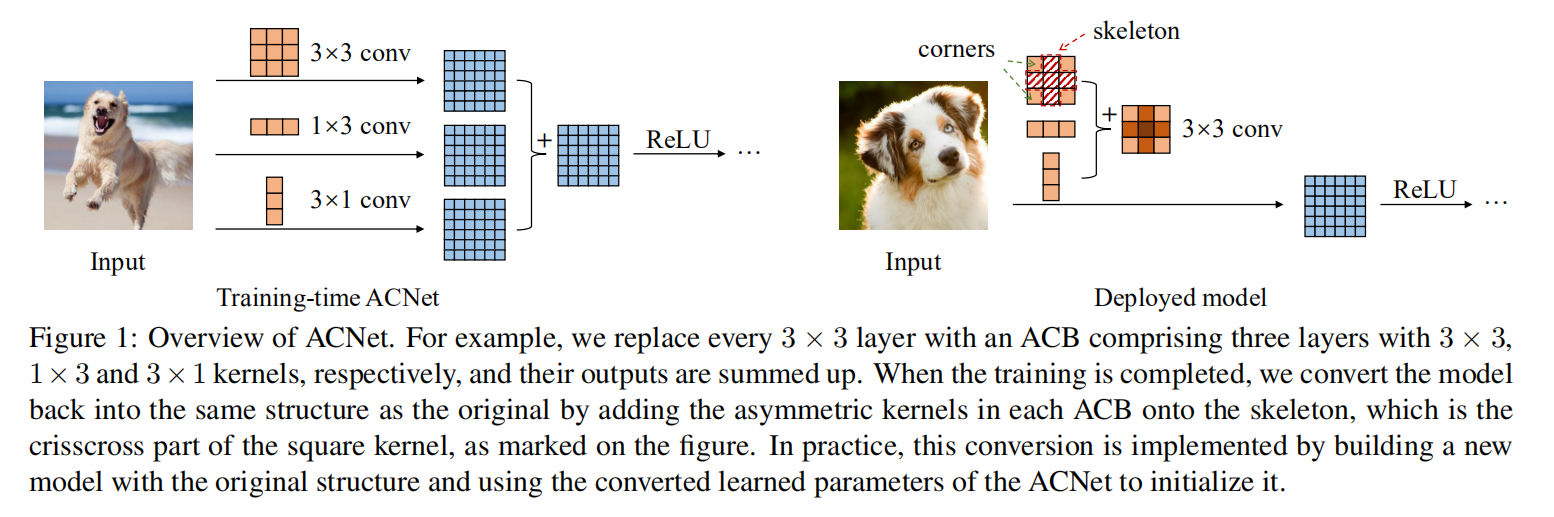
- 假定标准卷积的核大小为
ACB构造了3个并行卷积,其核大小分别为- 每个卷积层之后跟随着一个
BN层; - 输入数据分别经过
3个卷积+BN的特征提取后,最后进行求和操作(以丰富特征空间)
推理阶段
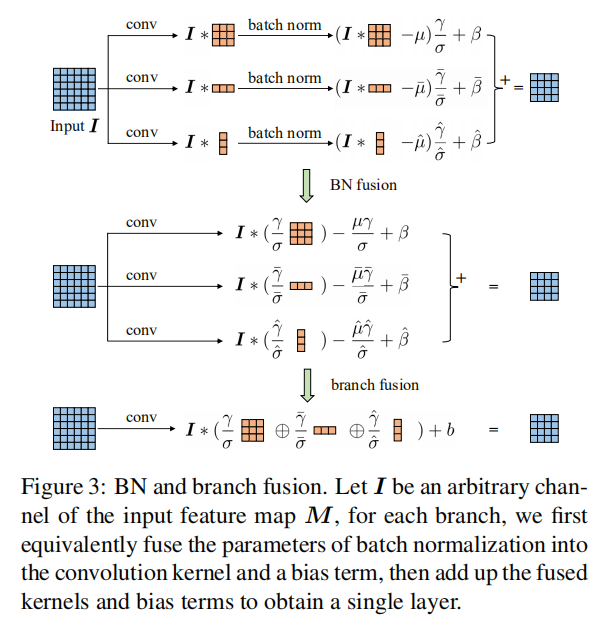
完成训练后,将ACB模块重新转换成标准卷积,从而在不增加额外计算量的情况下提高模型泛化性能。共分为两步实现:
BN融合(BN fusion):融合同一分支下的Conv+BN -> Conv- 分支融合(
branch fusion):融合多条分支的Conv
BN融合
设置
分支融合
通过上述转换后,可以得到
实验
通过实验证明了ACB能够有效的在多个不同数据集(CIFAR10/CIFAR100/ImageNet)上提升模型(VGG/ResNet/WRN/DenseNet)性能
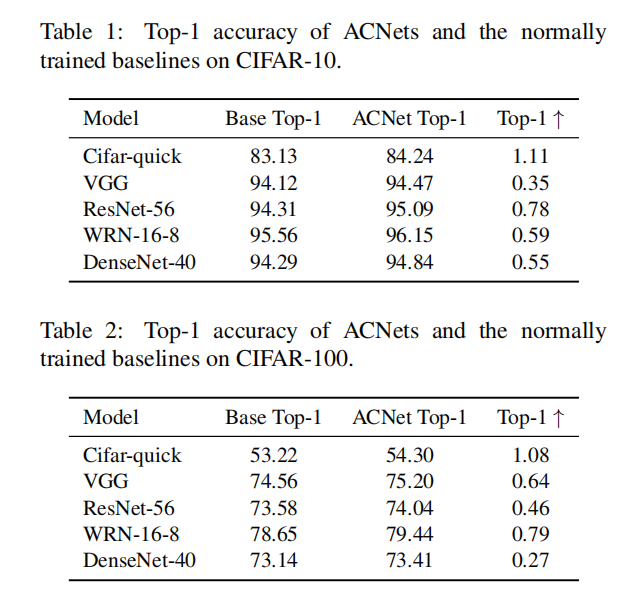

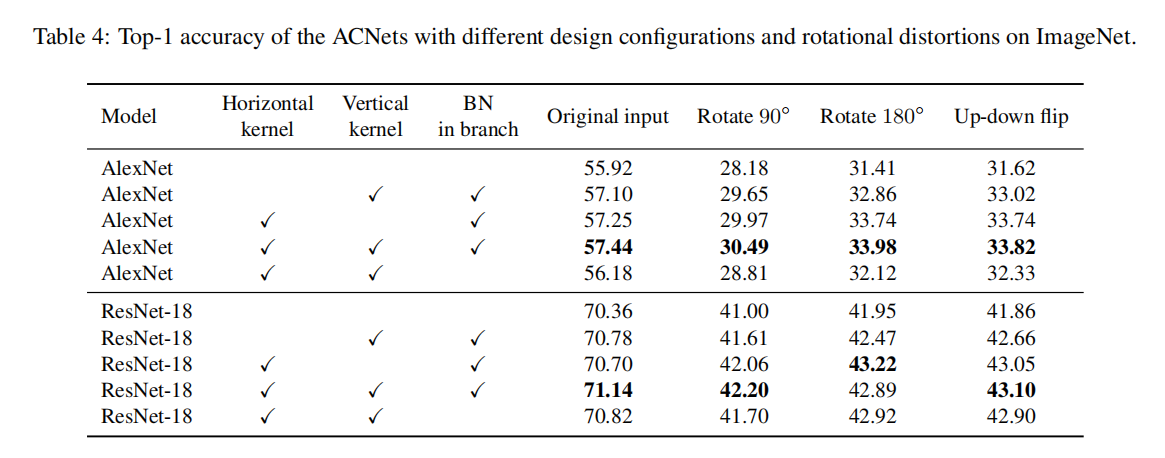
消融研究
通过实验证明了水平卷积核、垂直卷积核以及BN的有效性
来做第一个留言的人吧!