k-means聚类算法

分类 vs. 聚类

分类：类别是已知的，通过对已知分类的数据进行训练和学习，找到这些不同类别的特征，再对未分类的数据进行分类。属于有监督学习（有标签） 聚类：事先不知道数据会分为几类，通过聚类分析将数据聚合成几个群体。聚类不需要对数据进行训练和学习。属于无监督学习（无标签）

k-means聚类

定义

k-means聚类算法通过计算距离作为相似度来衡量两个对象是否属于同一簇。其算法如下：

1. 随机选取\(k\)个对象作为初始聚类中心
2. 计算所有对象和这\(k\)个聚类中心的距离（欧式距离），将其分配给距离最近的聚类中心
3. 完成所有对象的分配后，重新计算这\(k\)个聚类的中心，重复第2步
4. 终止条件：
   1. 没有（或最小数目）对象被重新分配给不同的聚类
   2. 没有（或最小数目）聚类中心发生变化
   3. 误差平方和局部最小

具体实现过程中，需要注意以下几点：

1. \(k\)是超参数，表明了本次实现要计算的类别数
2. 通过计算\(k\)个聚类的均值来重新确定聚类中心。注意：此时的聚类中心可能就不是某一个对象了

实现

百度百科给出了很好的实现范例：

class KMeansClusterer:

    def __init__(self, ndarray, cluster_num):
        self.ndarray = ndarray
        self.cluster_num = cluster_num
        self.points = self.__pick_start_point(ndarray, cluster_num)

    def cluster(self):
        result = []
        for i in range(self.cluster_num):
            result.append([])
        for item in self.ndarray:
            distance_min = sys.maxsize
            index = -1
            for i in range(len(self.points)):
                distance = self.__distance(item, self.points[i])
                if distance < distance_min:
                    distance_min = distance
                    index = i
            result[index] = result[index] + [item.tolist()]
        new_center = []
        for item in result:
            new_center.append(self.__center(item).tolist())
        # 中心点未改变，说明达到稳态，结束递归
        if (self.points == new_center).all():
            return result

        self.points = np.array(new_center)
        return self.cluster()

    def __center(self, list):
        '''
        计算一组坐标的中心点
        '''
        # 计算每一列的平均值
        return np.array(list).mean(axis=0)

    def __distance(self, p1, p2):
        '''
        计算两点间距
        '''
        tmp = 0
        for i in range(len(p1)):
            tmp += pow(p1[i] - p2[i], 2)
        return pow(tmp, 0.5)

    def __pick_start_point(self, ndarray, cluster_num):

        if cluster_num < 0 or cluster_num > ndarray.shape[0]:
            raise Exception("簇数设置有误")

        # 随机点的下标
        indexes = random.sample(np.arange(0, ndarray.shape[0], step=1).tolist(), cluster_num)
        points = []
        for index in indexes:
            points.append(ndarray[index].tolist())
        return np.array(points)

距离计算

k-means聚类算法通过欧式距离来衡量对象和聚类中心的相似度。对于多属性的对象而言，选择哪些属性参与距离计算也是一个很好的优化方法

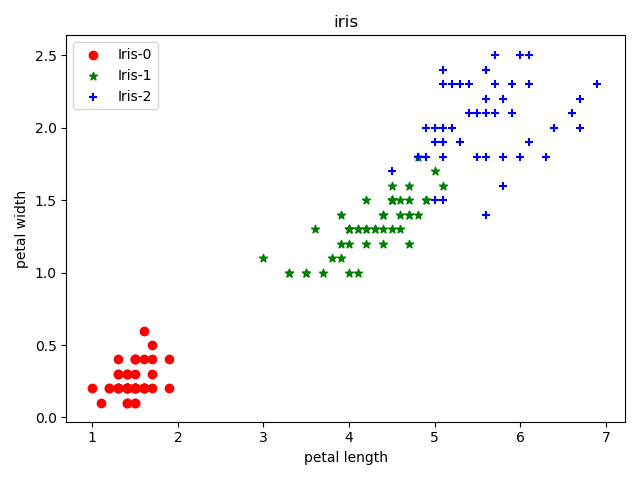
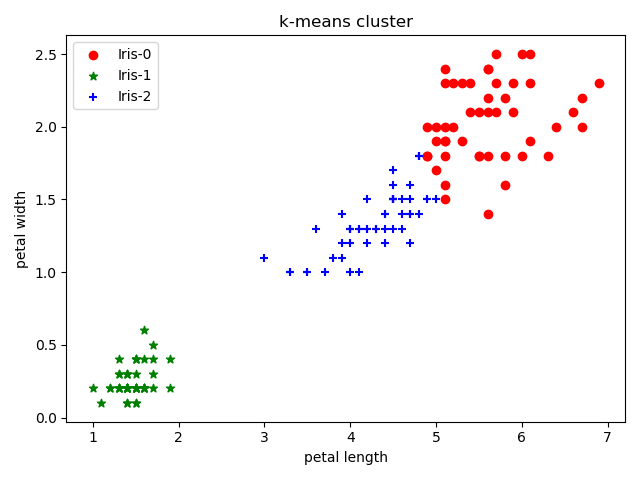
示例：iris分类

使用k-means聚类算法分类iris数据集

数据集定义

iris数据集包含了4个属性，分别表示（单位cm）：

1. 萼片(sepal)长度
2. 萼片宽度
3. 花瓣(petal)长度
4. 花瓣宽度

每个类别有50个实例，整个数据集共150个

sklearn实现

sklearn提供了k-means算法，实现iris聚类

from sklearn import datasets
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans


def load_data():
    # Import some data to play with
    iris = datasets.load_iris()
    X = iris.data
    y = iris.target

    return X, y


def plot(data, target, title='iris'):
    x0 = data[target == 0]
    x1 = data[target == 1]
    x2 = data[target == 2]

    fig = plt.figure()
    plt.title(title)
    plt.scatter(x0[:, 0], x0[:, 1], c="red", marker='o', label='Iris-0')
    plt.scatter(x1[:, 0], x1[:, 1], c="green", marker='*', label='Iris-1')
    plt.scatter(x2[:, 0], x2[:, 1], c="blue", marker='+', label='Iris-2')
    plt.xlabel('petal length')
    plt.ylabel('petal width')
    plt.legend(loc=2)
    plt.show()


if __name__ == '__main__':
    data, target = load_data()
    plot(data, target)

    # 构造聚类器
    estimator = KMeans(n_clusters=3)
    # 聚类
    estimator.fit(data)
    # 获取聚类标签
    label_pred = estimator.labels_
    plot(data, label_pred, title='k-means cluster')

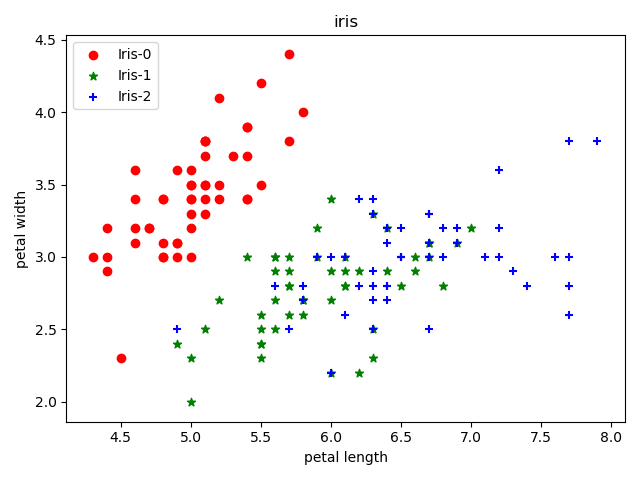
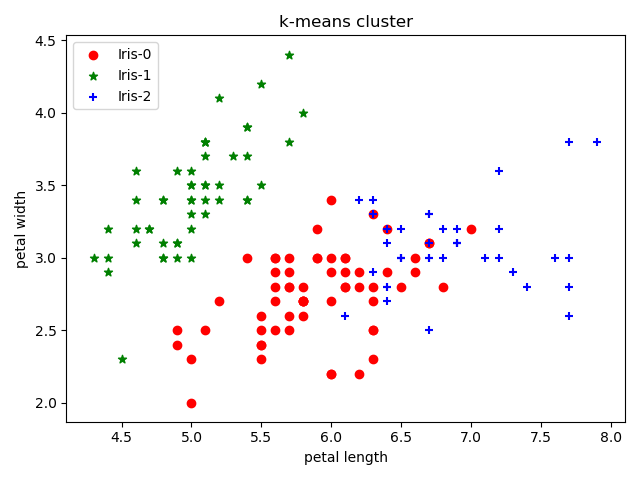
上述结果使用了iris的4个属性进行聚类下面仅使用后两个属性进行聚类

if __name__ == '__main__':
    data, target = load_data()
    data = data[:, 2:]
    plot(data, target)

    # 构造聚类器
    estimator = KMeans(n_clusters=3)
    # 聚类
    estimator.fit(data)
    # 获取聚类标签
    label_pred = estimator.labels_
    plot(data, label_pred, title='k-means cluster')

相关阅读

• K均值聚类算法

• 5 分钟带你弄懂 k-means 聚类

• [数据集]Iris

• 利用python内置K-Means聚类算法实现鸢尾花数据的聚类