正态分布

发表于 更新于 分类于
本文字数： 1k 阅读时长 ≈ 2 分钟

正态分布（normal distribution），也称为常态分布，高斯分布（gaussian distribution），是连续随机变量概率分布的一种，自然界中大量现象符合正态分布，比如身高/体重/成绩/收入/寿命

一维正态分布

若随机变量\(X\)服从一个位置参数（数学期望）为\(\mu\)、尺度参数（方差）为$$的概率分布，且其概率密度函数为

\[ f(x)=\frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{(x-\mu)^{2}}{2 \sigma^{2}}\right) \]

则这个随机变量就称为正态随机变量，正态随机变量服从的分布就称为正态分布，记作\(X \sim N\left(\mu, \sigma^{2}\right)\)

标准正态分布

当\(\mu =0, \sigma =1\)的正态分布称为标准正态分布

特性

  • 期望值\(\mu\)决定了概率密度函数的分布位置，离\(\mu\)近的值概率大，反之概率小

  • 正态分布以\(\mu\)为对称轴，左右完全对称；正态分布的期望、均数、中位数和总数都是\(\mu\)

  • 方差\(\sigma\)决定了分布幅度大小（离散程度），\(\sigma\)越大，数据分布越分散，曲线越扁平；反之，数据越集中，曲线越廋高

  • 通常称发生概率小于5%的事件几乎不可能发生，在\(\left ( \mu-3\cdot \sigma,\mu+3\cdot \sigma \right )\)区间外的概率小于千分之三，所以基本上把区间\(\left ( \mu-3\cdot \sigma,\mu+3\cdot \sigma \right )\)称为随机变量x实际可能的取值范围，称为正态分布的\(3\sigma\)原则

  • 中心极限定理：多个独立分布的随机变量的和的均值服从正态分布

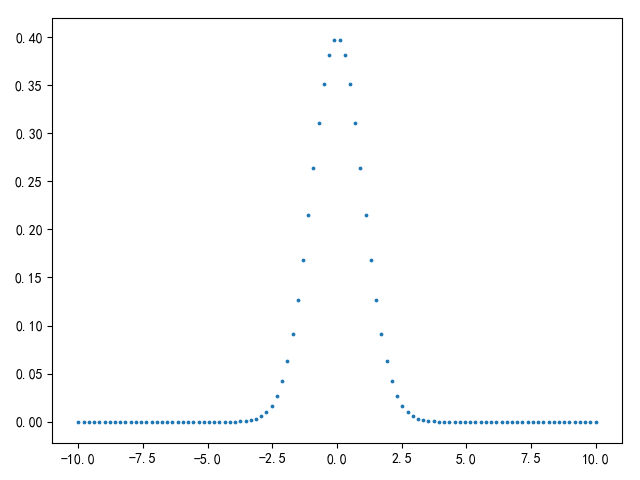
示例

参考python pylab plot normal distribution，标准正态分布如下

1
2
3
4
5
6
7
8
9
10
11
import matplotlib.pyplot as plt
import numpy as np
import scipy.stats as stats

if __name__ == '__main__':
    mu = 0
    variance = 1
    
    x = np.linspace(-10, 10, 100)
    plt.scatter(x, stats.norm.pdf(x, mu, variance), s=3)
    plt.show()

相关阅读