Distilling Knowledge via Knowledge Review
原文地址：Distilling Knowledge via Knowledge Review
复现地址：ZJCV/KnowledgeReview
摘要
Knowledge distillation transfers knowledge from the teacher network to the student one, with the goal of greatly improving the performance of the student network. Previous methods mostly focus on proposing feature transformation and loss functions between the same level's features to improve the effectiveness. We differently study the factor of connection path cross levels between teacher and student networks, and reveal its great importance. For the first time in knowledge distillation, cross-stage connection paths are proposed. Our new review mechanism is effective and structurally simple. Our finally designed nested and compact framework requires negligible computation overhead, and outperforms other methods on a variety of tasks. We apply our method to classification, object detection, and instance segmentation tasks. All of them witness significant student network performance improvement. Code is available at this https URL
知识蒸馏将知识从教师网络转移到学生网络，目的是大大提高学生网络的性能。以往的方法大多侧重于提出同级特征之间的特征变换和损失函数，以提高有效性。相反，我们研究了对师生网络之间不同级别路径连接并揭示了其重要性。在知识蒸馏中，这是首次提出跨级连接路径。我们新设计的复习机制高效并且结构简单。我们最终设计的嵌套且紧凑的框架所需的计算开销可以忽略不计，并且在各种任务上优于其他方法。将我们的方法应用于分类、目标检测和实例分割任务，所有这些实验都显著提高了学生网络性能。代码开源在https://github.com/dvlab-research/ReviewKD
思路
在之前的知识迁移算法中，往往使用同一级别特征进行特征蒸馏训练，比如使用教师网络第4组的特征来训练学生网络第4组的特征。论文发现这个现象，设计了垮级连接训练方式，尝试了使用教师网络低级特征来训练学生网络更深级别的特征，从试验结果看更好的提升了学生网络性能。
论文与人类学习曲线（Historical review and comprehensive survey）进行了类比，幼年期的学生只能理解一小部分知识，在成长的过程中，越来越多过去的知识可能会逐渐被理解和保存为经验。
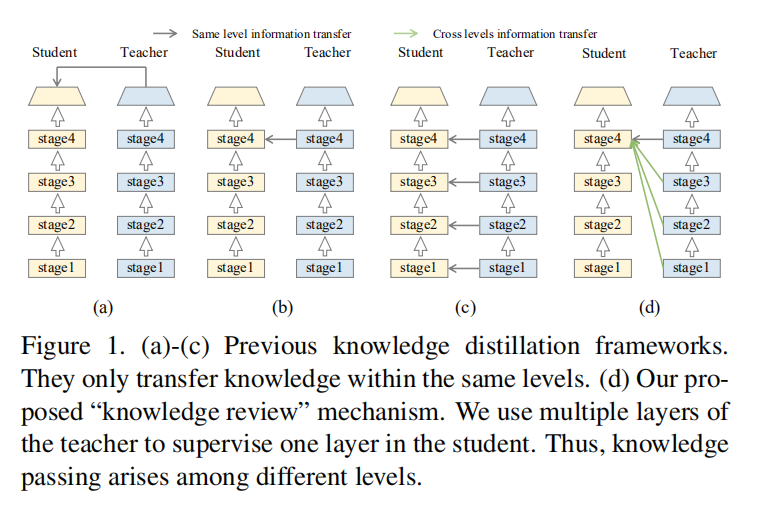
论文提出的知识复习框架如上图（d）所示，将教师网络多级特征同时应用于学生网络单级特征学习中。
复习机制
传统范式
给定输入图像\(X\)和学生网络\(S\)，那么学生网络的输出向量可以计算为
\[ Y_{s}=S(X) \]
细分学生网络\(S\)得到\((S_{1}, S_{2}, ..., S_{n}, S_{c})\)，其中\(S_{c}\)表示分类器，其余\(S_{1}, ..., S_{n}\)表示各个中间层。所以输出向量的计算可以修改为
\[ Y_{s} = S_{c} ◦S_{n} ◦ · · ·◦S_{1}(X) \]
- \(◦\)表示嵌套函数，\(g◦f(x) = g(f(x))\)
各个中间层计算的特征设定为\((F_{s}^{1}, ..., F_{s}^{n})\)，第\(i\)个特征计算如下：
\[ F_{s}^{i} = S_{i} ◦ · · ·◦S_{1}(X) \]
对于单层知识蒸馏而言，其公式表示如下：
\[ L_{SKD} = D(M_{s}^{i}(F_{s}^{i}), M_{t}^{i}(F_{t}^{i})) \]
- 上述公式表示对教师网络和学生网络的第\(i\)层特征进行蒸馏训练；
- \(M_{s}^{i}\)表示学生网络第\(i\)层的特征转换；
- \(F_{s}^{i}\)表示学生网络第\(i\)层输出的特征向量；
- \(D\)表示距离函数。
对于多层知识蒸馏而言，其公式描述如下：
\[ L_{MKD} = \sum_{i\in I} D(M_{s}^{i}(F_{s}^{i}), M_{t}^{i}(F_{t}^{i})) \]
- \(I\)表示待训练的多级特征集合。
知识复习
在论文设计的知识复习框架中，使用之前层的特征对当前层特征进行训练。其单层知识蒸馏可以归纳如下：
\[ L_{SKD\_R} = \sum_{j=1}^{i}D(M_{s}^{i,j}(F_{s}^{i}), M_{t}^{i,j}(F_{t}^{j})) \]
- \(M_{s}^{i,j}\)表示学生网络针对第\(i\)层输出特征，用于匹配教师网络第\(j\)层特征的转换函数；
- \(M_{t}^{i,j}\)表示教师网络针对第\(j\)层输出特征，用于匹配学生网络第\(i\)层特征的转换函数。
对于第\(i\)层学生网络特征，使用第\(1\)到\(i\)层的教师网络进行训练。注意：\(1 \leq j\leq i\)
对于多层知识蒸馏，其公式描述如下：
\[ L_{MKD\_R} = \sum_{i\in I}(\sum_{j=1}^{i}D(M_{s}^{i,j}(F_{s}^{i}), M_{t}^{i,j}(F_{t}^{j}))) \]
也就是说，遍历学生网络的第\(1\)到\(I\)层特征，每层学生网络特征均使用教师网络的第\(1\)到\(i\)层特征进行训练。
转换函数
对于知识迁移算法而言，转换函数可划分为两类：教师转换和学生转换。其分别作用于教师网络特征和学生网络特征，其目的在于保证两者特征具有相同大小，以进行知识迁移训练
教师转换
论文不对教师网络特征进行操作，需要学生网络特征转换到对应教师网络特征大小。
学生转换
因为学生网络每层待迁移的特征均对应于教师网络多层特征，所以论文设计了一个残差学习框架来帮助实现学生特征转换，如下图所示
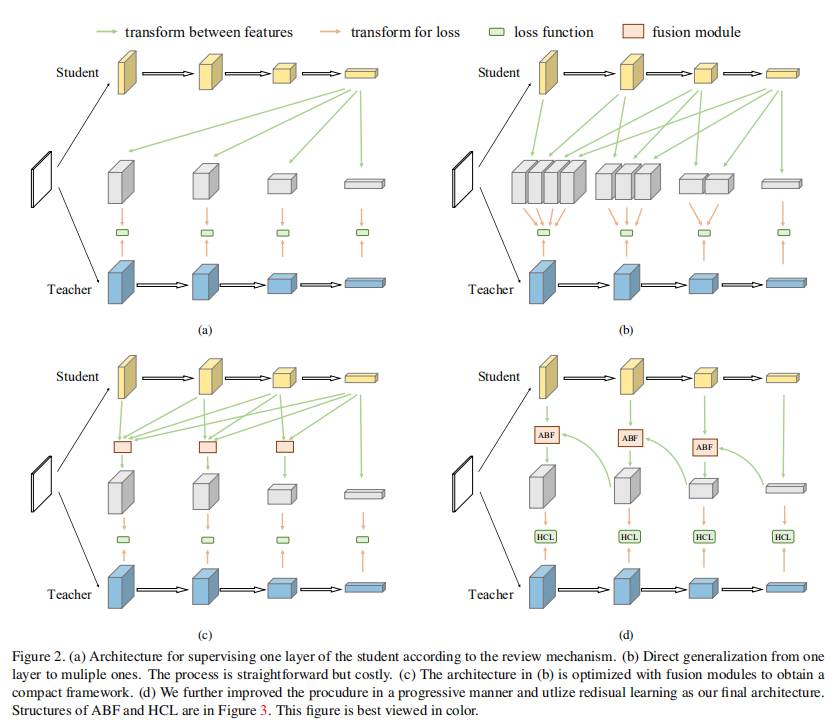
如上图（a）所示，第\(i\)层学生特征分别转换到第\(1\)到\(i\)层教师特征，论文设计的转换函数\(M_{s}^{i,j}\)由卷积层和上采样层组成，将第\(i\)层学生网络特征大小转换到和第\(j\)层教师网络相同大小。完整实现即上图（b）所示，假定网络共训练\(n\)层特征，那么需要进行\(n(n+1)/2\)次学生特征转换。为此，论文重新设计了学生特征转换实现，首先按照之前描述，计算知识迁移的损失公式如下：
\[ L_{MKD\_R}=\sum_{i=1}^{n}(\sum_{j=1}^{i}D(F_{s}^{i}, F_{t}^{j})) \]
- \(D\)表示学生特征和教师特征的距离函数；
- 对于第\(i\)层学生特征，需要计算它与第\(1\)到\(i\)层教师特征的损失。
切换变量\(i\)和\(j\)的求和顺序，公式如下：
\[ L_{MDK\_R}=\sum_{j=1}^{n}(\sum_{i=j}^{n}D(F_{s}^{i}, F_{t}^{j})) \]
固定变量\(j\)时，上式可看成是计算教师特征\(F_{t}^{j}\)和学生特征\(F_{s}^{j} - F_{s}^{n}\)之间的距离，可以近似看成是教师特征\(F_{t}^{j}\)和学生融合特征之间的距离，公式如下：
\[ \sum_{i=j}^{n}D(F_{s}^{i}, F_{t}^{j}) \approx D(u(F_{s}^{j}, ..., F_{s}^{n}), F_{t}^{j}) \]
- \(u\)表示特征融合函数
整体实现如上图（c）所示，添加了一个融合模块。论文再次进行了简化操作，将\(F_{s}^{j}, ..., F_{s}^{n}\)之间的融合操作简化为\(F_{s}^{j}\)和\(u(F_{s}^{j+1}, ..., F_{s}^{n})\)之间的融合，所以可以从后往前递归计算\(u(\cdot, \cdot)\)，计算公式如下：
\[ L_{MKD\_R}=D(F_{s}^{n}, F_{t}^{n}) + \sum_{j=n-1}^{1}D(u(F_{s}^{j}, F_{s}^{j+1,n}), F_{t}^{j}) \]
如上图（d）所示，上述操作类似于残差连接。通过上述转换，整体的计算步骤减少到\(n\)次即可完成。
ABF & HCL
在上图（d）中，为了提高知识迁移的性能，论文额外增加了两个模块：ABF（attention based fusion）和HCL（hierarchical context loss），分别作用于学生特征融合以及教师-学生特征距离计算。整体架构如下图所示
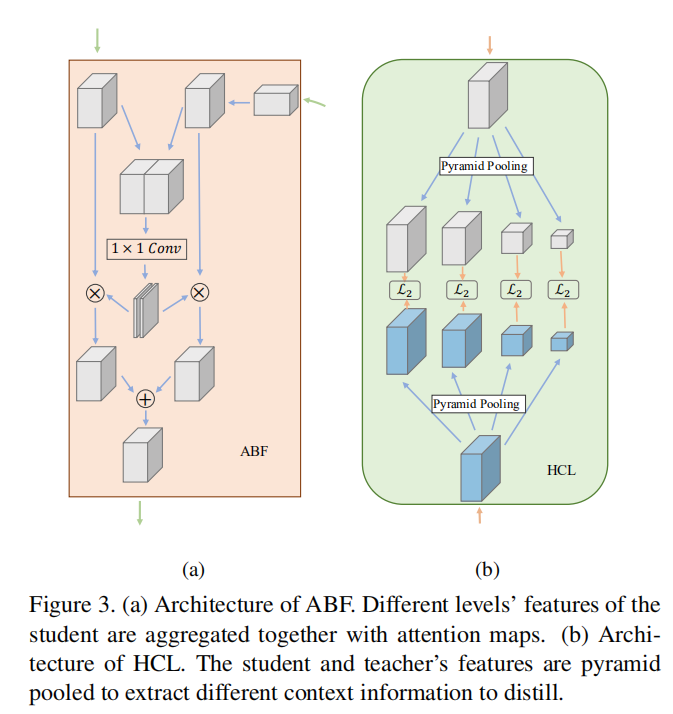
ABF
- 缩放高维特征，保持和低维特征相同大小；
- 两个不同级别的学生特征连接在一起（\(2\times H\times W\)），生成注意力图（保持大小和数量不变）；
- 将生成的注意力图分别与两个特征进行融合（相乘操作）；
- 最后，融合（相加操作）两层特征得到最终的学生特征。
HCL
论文考虑到和教师特征进行距离计算的学生特征是不同级别（最直观：感受野大小不同）的特征融合得到，所以
- 使用金字塔池化操作获取不同大小的教师－学生特征；
- 成对计算\(L2\)距离；
- 最后求和得到最终的损失。
损失函数
知识复习算法是一阶段蒸馏训练，结合蒸馏损失和正常的任务损失一起进行训练，其公式如下：
\[ L = L_{CE} + \lambda L_{MKD\_R} \]
论文实验中发现，使用更浅的教师特征去监督更深的学生特征能够得到很好的性能增益，而相反的方式并不会得到非常好的提升效果。论文解释是因为更深的、更加抽象的特征对于早期学习而言太过于复杂了。
实验
CIFAR100
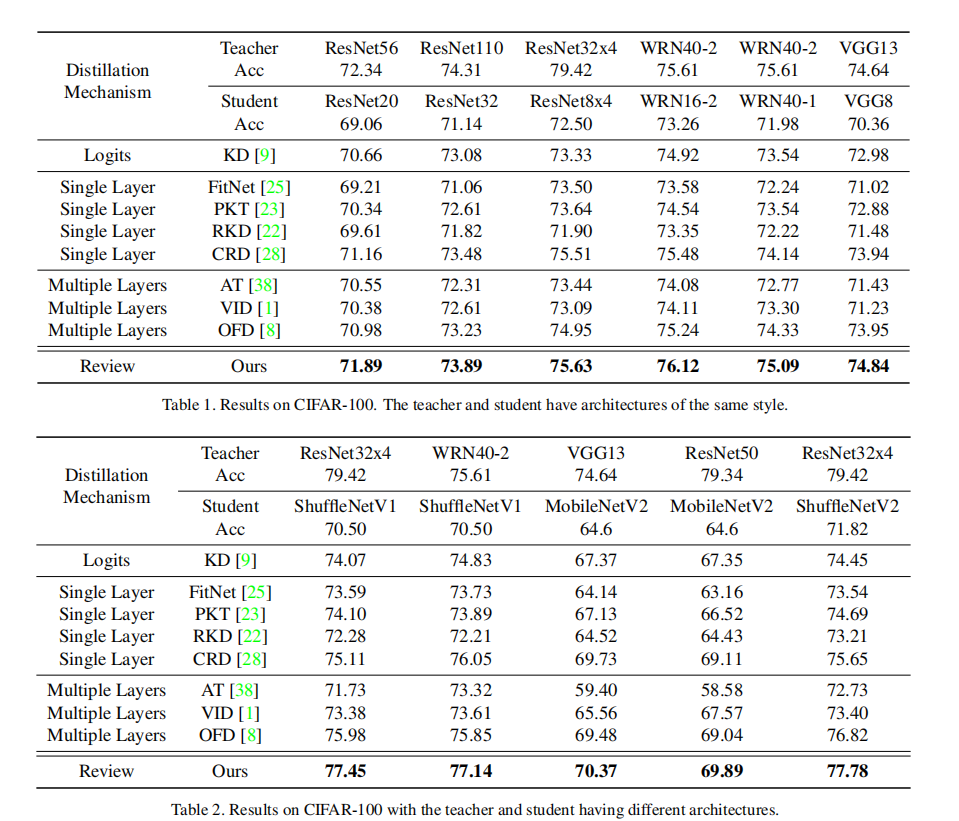
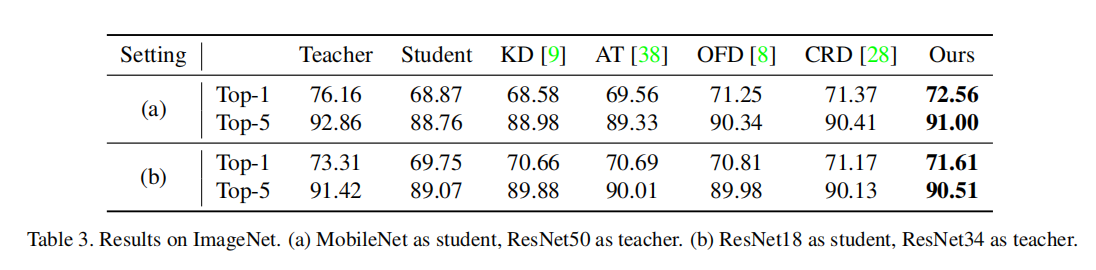
ImageNet
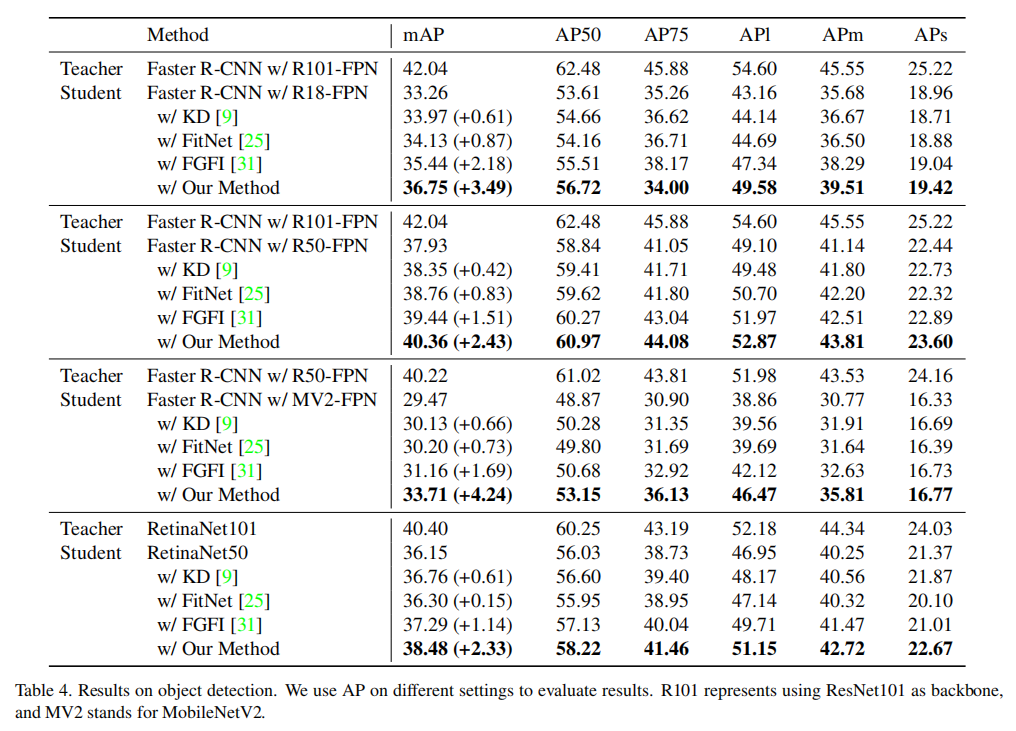
目标检测
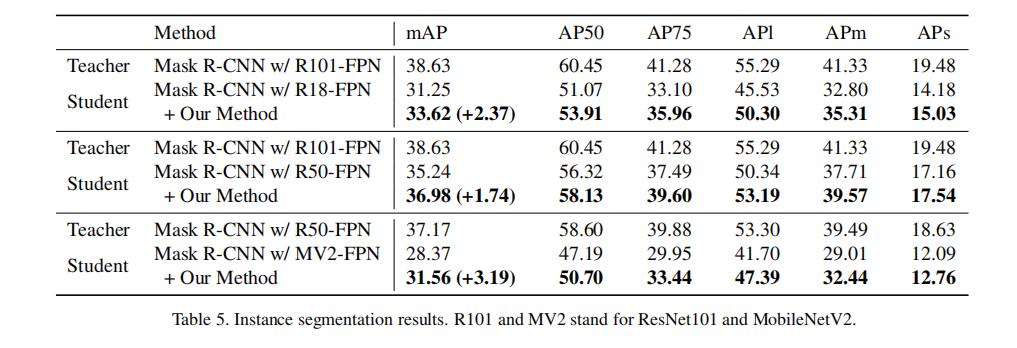
目标分割
分析
跨阶段作用
论文使用ResNet20作为学生网络，使用ResNet56作为教师网络，在CIFAR100数据集进行实验，分析跨阶段知识迁移作用。实验设置如下：共采集\(4\)个阶段特征进行实验；选定学生网络进行训练的阶段数目，然后变化教师网络的迁移阶段数目。实验结果如下表所示：
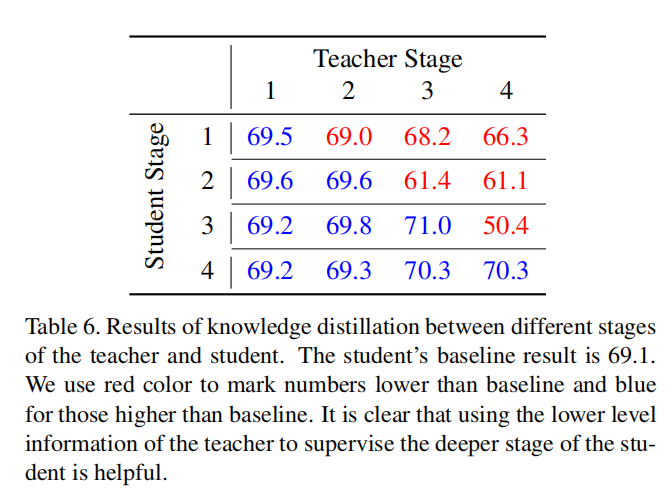
在上图中，红色数值表示结果低于baseline，蓝色数值表示结果高于baseline。从结果可以发现
- 跨阶段特征有助于知识迁移；
- 教师高级别特征不利于学生低级别特征训练。
论文给出一个解释是教师网络高级别抽象知识对于学生网络低级别边缘特征学习。
消融研究
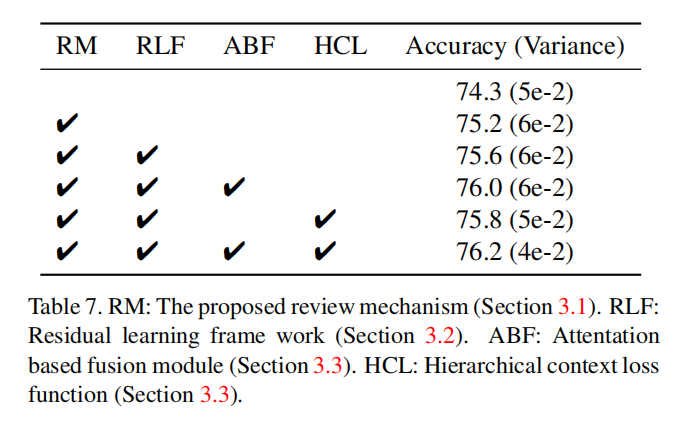
论文也分别研究了所提出的各个模块对于性能的增益，如下表所示：
小结
论文主要内容：
- 使出一种新的知识蒸馏算法，利用教师网络多级特征同时指导学生网络单级特征学习；
- 提出一个残差学习框架（
residual learning framework）进行学生特征转换； - 提出一个基于融合的注意力（
attentation based fusion (ABF)）模块以及一个层次上下文损失（hierarchical context loss (HCL)）函数来辅助学习；
总的来说，RFD的整体框架非常类似于OFD的实现，并且提出了跨阶段知识迁移概念，以及通过残差学习架构简化学生特征转换，同时利用ABF和HCL的使用包含了分离-融合-选择的思想。