[译]Rethinking the Inception Architecture for Computer Vision
原文地址:Rethinking the Inception Architecture for Computer Vision
Abstract
摘要
Convolutional networks are at the core of most state-of-the-art computer vision solutions for a wide variety of tasks. Since 2014 very deep convolutional networks started to become mainstream, yielding substantial gains in various benchmarks. Although increased model size and computational cost tend to translate to immediate quality gains for most tasks (as long as enough labeled data is provided for training), computational efficiency and low parameter count are still enabling factors for various use cases such as mobile vision and big-data scenarios. Here we are exploring ways to scale up networks in ways that aim at utilizing the added computation as efficiently as possible by suitably factorized convolutions and aggressive regularization. We benchmark our methods on the ILSVRC 2012 classification challenge validation set demonstrate substantial gains over the state of the art: 21.2% top-1 and 5.6% top-5 error for single frame evaluation using a network with a computational cost of 5 billion multiply-adds per inference and with using less than 25 million parameters. With an ensemble of 4 models and multi-crop evaluation, we report 3.5% top-5 error and 17.3% top-1 error.
卷积网络是用于各种任务的最先进的计算机视觉解决方案的核心。自2014年以来,极深卷积网络开始成为主流,在各种基准测试中取得很好的成绩。尽管增加的模型大小和计算成本往往会转化为大多数任务的即时质量收益(只要为训练提供足够的标记数据),但计算效率和低参数总数仍然是各种用例(如移动视觉和大数据场景)的有利因素。在这里,我们正在探索扩大网络规模的方法,目的是通过适当的因子分解卷积和积极的正则化尽可能有效地利用增加的计算。我们在ILSVRC 2012分类挑战验证集上对我们的方法进行了基准测试,结果表明,我们的方法在当前技术水平上取得了显著的进步:对于单帧评估,前1名误差为21.2%,前5名误差为5.6%,使用的网络计算成本为50亿次乘加,每次推理使用的参数少于2500万个。通过4个模型的集成和多裁剪评估,我们得到了3.5%的前5名误差和17.3%的前1名误差
Introduction
引言
Since the 2012 ImageNet competition [16] winning entry by Krizhevsky et al [9], their network “AlexNet” has been successfully applied to a larger variety of computer vision tasks, for example to object-detection [5], segmentation [12], human pose estimation [22], video classification [8], object tracking [23], and superresolution [3].
自从2012年ImageNet比赛以来,Krizhevsky等人实现的AlexNet模型已成功的应用于许多计算机视觉任务,比如目标检测[5]、分割[12]、人类姿势估计[22]、视频分类[8]、目标追踪[23]以及超分辨率重建[3]
These successes spurred a new line of research that focused on finding higher performing convolutional neural networks. Starting in 2014, the quality of network architectures significantly improved by utilizing deeper and wider networks. VGGNet [18] and GoogLeNet [20] yielded similarly high performance in the 2014 ILSVRC [16] classification challenge. One interesting observation was that gains in the classification performance tend to transfer to significant quality gains in a wide variety of application domains. This means that architectural improvements in deep convolutional architecture can be utilized for improving performance for most other computer vision tasks that are increasingly reliant on high quality, learned visual features. Also, improvements in the network quality resulted in new application domains for convolutional networks in cases where AlexNet features could not compete with hand engineered, crafted solutions, e.g. proposal generation in detection[4].
这些成功激发了一个新的研究方向,集中于寻找性能更高的卷积神经网络。从2014年开始,通过利用更深更宽的网络,网络体系结构的质量显著提高。VGGNet [18]和GoogLeNet [20]在2014年ILSVRC [16]分类挑战中取得了类似的高性能。一个有趣的观察结果是,在广泛的应用领域中,分类性能的提高往往会转化为其它应用领域显著的质量提高。这意味着深度卷积体系结构中的体系结构改进可以用于提高大多数其他计算机视觉任务的性能,这些任务越来越依赖于高质量的、经过学习的视觉特征。此外,网络质量的提高为卷积网络带来了新的应用领域,在这种情况下,AlexNet的特性无法与人为设计的解决方案相竞争,例如检测中的建议生成[4]
Although VGGNet [18] has the compelling feature of architectural simplicity, this comes at a high cost: evaluating the network requires a lot of computation. On the other hand, the Inception architecture of GoogLeNet [20] was also designed to perform well even under strict constraints on memory and computational budget. For example, GoogleNet employed only 5 million parameters, which represented a 12× reduction with respect to its predecessor AlexNet, which used 60 million parameters. Furthermore, VGGNet employed about 3x more parameters than AlexNet.
尽管VGGNet [18]具有引人注目的结构简单性,但这需要很高的成本:评估网络需要大量的计算。另一方面,GoogLeNet[20]的Inception架构也被设计成即使在内存和计算预算的严格限制下也能运行良好。例如,GoogleNet仅使用了500万个参数,与使用了6000万个参数的前身AlexNet相比,减少了12倍。此外,VGGNet使用的参数比AlexNet多3倍
The computational cost of Inception is also much lower than VGGNet or its higher performing successors [6]. This has made it feasible to utilize Inception networks in big-data scenarios[17], [13], where huge amount of data needed to be processed at reasonable cost or scenarios where memory or computational capacity is inherently limited, for example in mobile vision settings. It is certainly possible to mitigate parts of these issues by applying specialized solutions to target memory use [2], [15] or by optimizing the execution of certain operations via computational tricks [10]. However, these methods add extra complexity. Furthermore, these methods could be applied to optimize the Inception architecture as well, widening the efficiency gap again.
Inception的计算成本也远低于VGGNet或其更高性能的后续实现[6]。这使得在大数据场景([17]、[13])中利用Inception网络成为可能,在这些场景中,需要以合理的成本处理大量数据,或者在内存或计算能力固定有限的场景中,例如在移动视觉环境中。通过使用[2],[15]对目标内存应用专门的解决方案,或者通过计算技巧优化某些操作的执行,当然有可能缓解部分问题[10]。然而,这些方法增加了额外的复杂性。此外,这些方法也可以用于优化Inception架构,再次扩大效率差距
Still, the complexity of the Inception architecture makes it more difficult to make changes to the network. If the architecture is scaled up naively, large parts of the computational gains can be immediately lost. Also, [20] does not provide a clear description about the contributing factors that lead to the various design decisions of the GoogLeNet architecture. This makes it much harder to adapt it to new use-cases while maintaining its efficiency. For example, if it is deemed necessary to increase the capacity of some Inception-style model, the simple transformation of just doubling the number of all filter bank sizes will lead to a 4x increase in both computational cost and number of parameters. This might prove prohibitive or unreasonable in a lot of practical scenarios, especially if the associated gains are modest. In this paper, we start with describing a few general principles and optimization ideas that that proved to be useful for scaling up convolution networks in efficient ways. Although our principles are not limited to Inception-type networks, they are easier to observe in that context as the generic structure of the Inception style building blocks is flexible enough to incorporate those constraints naturally. This is enabled by the generous use of dimensional reduction and parallel structures of the Inception modules which allows for mitigating the impact of structural changes on nearby components. Still, one needs to be cautious about doing so, as some guiding principles should be observed to maintain high quality of the models.
尽管如此,Inception架构的复杂性使得对网络进行更改更加困难。如果架构被简单地放大,很大一部分计算收益可能会立即丢失。此外,[20]并没有提供一个清晰的描述,关于影响GoogLeNet架构的各种设计决策的因素。例如,如果认为有必要增加一些Inception样式模型的容量,那么将所有滤波器组大小的数量增加一倍的简单转换将导致计算成本和参数数量增加4倍。在许多实际情况下,这可能被证明是禁止的或不合理的,特别是如果相关的收益是有限的情况下。在本文中,我们首先描述了一些通用的原则和优化思想,这些原则和优化思想被证明对以有效的方式扩展卷积网络是有用的。尽管我们的原则并不局限于Inception类型的网络,但是在这种情况下它们更容易被观察到,因为Inception风格构建块的一般结构足够灵活,可以自然地包含那些约束。这是通过Inception模块大量使用尺寸缩减和平行结构实现的,这允许减轻结构变化对周围组件的影响。尽管如此,我们还是需要谨慎行事,因为应该遵循一些指导原则来保持模型的高质量。
General Design Principles
通用设计准则
Here we will describe a few design principles based on large-scale experimentation with various architectural choices with convolutional networks. At this point, the utility of the principles below are speculative and additional future experimental evidence will be necessary to assess their accuracy and domain of validity. Still, grave deviations from these principles tended to result in deterioration in the quality of the networks and fixing situations where those deviations were detected resulted in improved architectures in general.
这里,我们将描述一些基于卷积网络的各种架构选择的大规模实验的设计原则。在这一点上,以下原则的效用是推测性的,未来需要额外的实验证据来评估其准确性和有效性范围。尽管如此,严重偏离这些原则往往会导致网络质量的恶化,而修复检测到这些偏离的情况通常会改善体系结构
- Avoid representational bottlenecks, especially early in the network. Feed-forward networks can be represented by an acyclic graph from the input layer(s) to the classifier or regressor. This defines a clear direction for the information flow. For any cut separating the inputs from the outputs, one can access the amount of information passing though the cut. One should avoid bottlenecks with extreme compression. In general the representation size should gently decrease from the inputs to the outputs before reaching the final representation used for the task at hand. Theoretically, information content can not be assessed merely by the dimensionality of the representation as it discards important factors like correlation structure; the dimensionality merely provides a rough estimate of information content.
- Higher dimensional representations are easier to process locally within a network. Increasing the activations per tile in a convolutional network allows for more disentangled features. The resulting networks will train faster.
- Spatial aggregation can be done over lower dimensional embeddings without much or any loss in representational power. For example, before performing a more spread out (e.g. 3 × 3) convolution, one can reduce the dimension of the input representation before the spatial aggregation without expecting serious adverse effects. We hypothesize that the reason for that is the strong correlation between adjacent unit results in much less loss of information during dimension reduction, if the outputs are used in a spatial aggregation context. Given that these signals should be easily compressible, the dimension reduction even promotes faster learning.
- Balance the width and depth of the network. Optimal performance of the network can be reached by balancing the number of filters per stage and the depth of the network. Increasing both the width and the depth of the network can contribute to higher quality networks. However, the optimal improvement for a constant amount of computation can be reached if both are increased in parallel. The computational budget should therefore be distributed in a balanced way between the depth and width of the network.
- 避免表示能力瓶颈,尤其是在网络早期。前馈网络可以由从输入层到分类器或回归器的非循环图来表示。这为信息流定义了一个清晰的方向。对于将输入和输出分开的任何切割,可以通过该切割访问信息。人们应该避免极度压缩的瓶颈。一般来说,在达到用于当前任务的最终表示之前,表示大小应该从输入到输出逐渐减小。从理论上讲,信息内容不能仅仅通过表征维度来评价,因为它抛弃了相关结构等重要因素;维度仅仅提供了对信息内容的粗略估计
- 高维表示更容易在网络中进行局部处理。在卷积网络中增加每个tile的激活允许更多的重要特征。由此产生的网络将训练得更快
- 空间聚合可以在低维嵌入上完成,而不会损失太多或任何的表示能力。例如,在执行更分散(例如3 × 3)的卷积之前,可以在空间聚集之前降低输入表示的维度,而不会预期严重的不利影响。我们假设其原因是,如果在空间聚合上下文中使用输出,则相邻单元之间的强相关性导致降维过程中的信息损失少得多。考虑到这些信号应该很容易压缩,降维甚至促进了更快的学习
- 平衡网络的宽度和深度。通过平衡每层滤波器的数量和网络的深度,可以达到网络的最佳性能。增加网络的宽度和深度有助于提高网络质量。然而,如果两者并行增加,则可以达到恒定计算量的最佳改进。因此,计算预算应该在网络的深度和宽度之间平衡分配
Although these principles might make sense, it is not straightforward to use them to improve the quality of networks out of box. The idea is to use them judiciously in ambiguous situations only.
虽然这些原则可能有意义,但使用它们来提高开箱即用网络的质量并不简单。这些想法适用于只能在模棱两可的情况
Factorizing Convolutions with Large Filter Size
分解大滤波器尺寸卷积
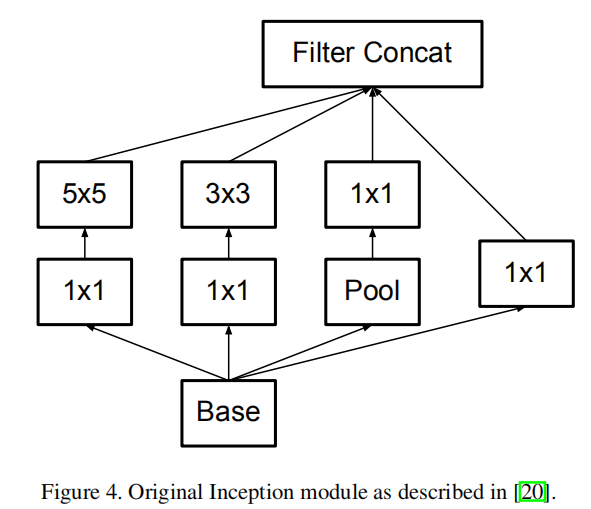
Much of the original gains of the GoogLeNet network [20] arise from a very generous use of dimension reduction. This can be viewed as a special case of factorizing convolutions in a computationally efficient manner. Consider for example the case of a 1 × 1 convolutional layer followed by a 3 × 3 convolutional layer. In a vision network, it is expected that the outputs of near-by activations are highly correlated. Therefore, we can expect that their activations can be reduced before aggregation and that this should result in similarly expressive local representations.
GoogLeNet网络[20]最初的大部分收益都来自于对降维的大量使用。这可以被看作是以有效计算方式分解卷积的特殊情况。例如,考虑1 × 1卷积层后跟3 × 3卷积层的情况。在视觉网络中,预期附近激活的输出是高度相关的。因此,我们可以预估这些激活可以在聚合之前被减少,并且这样也能得到相似的局部表示能力
Here we explore other ways of factorizing convolutions in various settings, especially in order to increase the computational efficiency of the solution. Since Inception networks are fully convolutional, each weight corresponds to one multiplication per activation. Therefore, any reduction in computational cost results in reduced number of parameters. This means that with suitable factorization, we can end up with more disentangled parameters and therefore with faster training. Also, we can use the computational and memory savings to increase the filter-bank sizes of our network while maintaining our ability to train each model replica on a single computer.
在这里,我们探索了在各种设置下分解卷积的其他方法,特别是为了提高解决方案的计算效率。由于Inception网络是全卷积的,每个权重对应于每次激活的一次乘法。因此,计算成本的任何降低都会导致参数数量的减少。这意味着有了合适的因式分解,我们可以得到更多解纠缠的参数,从而得到更快的训练。此外,我们可以利用计算和内存节省来增加我们网络的滤波器组大小,同时保持我们在单台计算机上训练每个模型副本的能力
Factorization into smaller convolutions
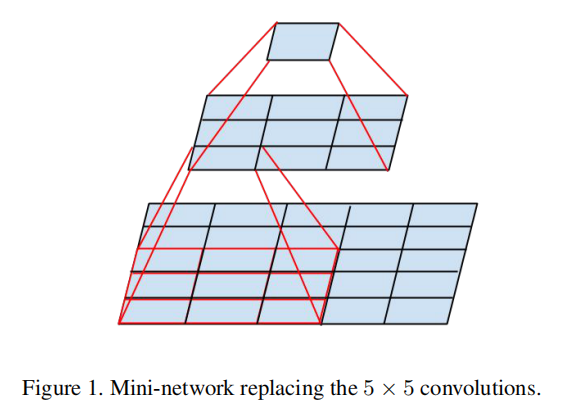
分解成更小的卷积
Convolutions with larger spatial filters (e.g. 5 × 5 or 7 × 7) tend to be disproportionally expensive in terms of computation. For example, a 5 × 5 convolution with n filters over a grid with m filters is 25/9 = 2.78 times more computationally expensive than a 3 × 3 convolution with the same number of filters. Of course, a 5×5 filter can capture dependencies between signals between activations of units further away in the earlier layers, so a reduction of the geometric size of the filters comes at a large cost of expressiveness. However, we can ask whether a 5 × 5 convolution could be replaced by a multi-layer network with less parameters with the same input size and output depth. If we zoom into the computation graph of the 5 × 5 convolution, we see that each output looks like a small fully-connected network sliding over 5×5 tiles over its input (see Figure 1). Since we are constructing a vision network, it seems natural to exploit translation invariance again and replace the fully connected component by a two layer convolutional architecture: the first layer is a 3 × 3 convolution, the second is a fully connected layer on top of the 3 × 3 output grid of the first layer (see Figure 1). Sliding this small network over the input activation grid boils down to replacing the 5 × 5 convolution with two layers of 3 × 3 convolution (compare Figure 4 with 5).
就计算而言,具有较大空间滤波器(例如5 × 5或7 × 7)的卷积往往过于昂贵。比如,生成m个网格,使用5x5大小卷积比使用3x3大小卷积多25/9=2.78倍。当然,一个5×5的滤波器可以捕捉早期层中更远单元的激活之间的信号相关性,因此滤波器的几何尺寸的减小是以高表达能力为代价的。然而,我们可以猜想在相同的输入大小和输出深度下,5 × 5卷积是否可以被具有较少参数的多层网络代替。如果我们放大5 × 5卷积的计算图,我们会看到每个输出看起来像一个小的全连接网络,在其输入上滑动5×5个tile(见图1)。因为我们正在构建一个视觉网络,所以再次利用平移不变性并用两层卷积结构替换完全连通的组件似乎是很自然的:第一层是3 × 3卷积,第二层是第一层的3 × 3输出网格之上的全连接层(见图1)。在输入激活网格上滑动这个小网络可以归结为用两层3 × 3卷积代替5 × 5卷积(比较图4和图5)。
This setup clearly reduces the parameter count by sharing the weights between adjacent tiles. To analyze the expected computational cost savings, we will make a few simplifying assumptions that apply for the typical situations: We can assume that n = αm, that is that we want to change the number of activations/unit by a constant alpha factor. Since the 5 × 5 convolution is aggregating, α is typically slightly larger than one (around 1.5 in the case of GoogLeNet). Having a two layer replacement for the 5 × 5 layer, it seems reasonable to reach this expansion in two steps: increasing the number of filters by √α in both steps. In order to simplify our estimate by choosing α = 1 (no expansion), If we would naivly slide a network without reusing the computation between neighboring grid tiles, we would increase the computational cost. sliding this network can be represented by two 3 × 3 convolutional layers which reuses the activations between adjacent tiles. This way, we end up with a net
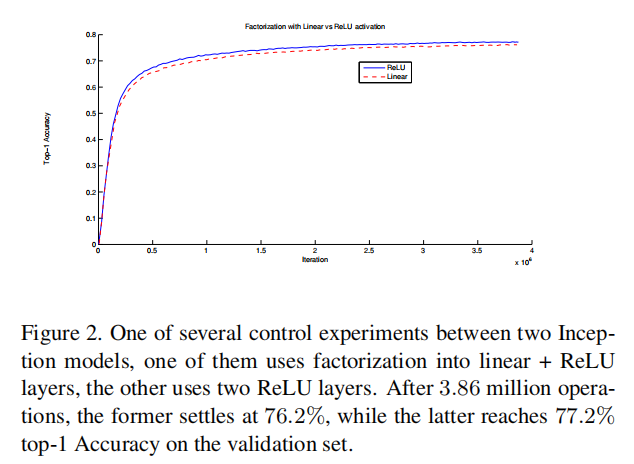
× reduction of computation, resulting in a relative gain of 28% by this factorization. The exact same saving holds for the parameter count as each parameter is used exactly once in the computation of the activation of each unit. Still, this setup raises two general questions: Does this replacement result in any loss of expressiveness? If our main goal is to factorize the linear part of the computation, would it not suggest to keep linear activations in the first layer? We have ran several control experiments (for example see figure 2) and using linear activation was always inferior to using rectified linear units in all stages of the factorization. We attribute this gain to the enhanced space of variations that the network can learn especially if we batchnormalize [7] the output activations. One can see similar effects when using linear activations for the dimension reduction components.
这种设置通过在相邻图块之间共享权重,明显减少了参数数目。为了分析预期的计算成本节约,我们将做出一些适用于典型情况的简化假设:我们可以假设n = αm,也就是说,我们想用一个常数α因子来改变激活次数/单位。由于5 × 5卷积正在聚集,α通常略大于1(在GoogLeNet的情况下约为1.5)。用两层代替5 × 5层,分两步实现这种扩展似乎是合理的: 在两个步骤中将滤波器数量增加√α。为了通过选择α = 1(无扩展)来简化我们的估计,如果我们滑动网络时不在相邻网格片之间重复计算,我们将增加计算成本。滑动该网络可以由两个3 × 3卷积层来表示,这两个卷积层重用相邻瓦片之间的激活。通过这种方式,我们最终实现了计算量的净减少
Spatial Factorization into Asymmetric Convolutions
非对称卷积的空间分解
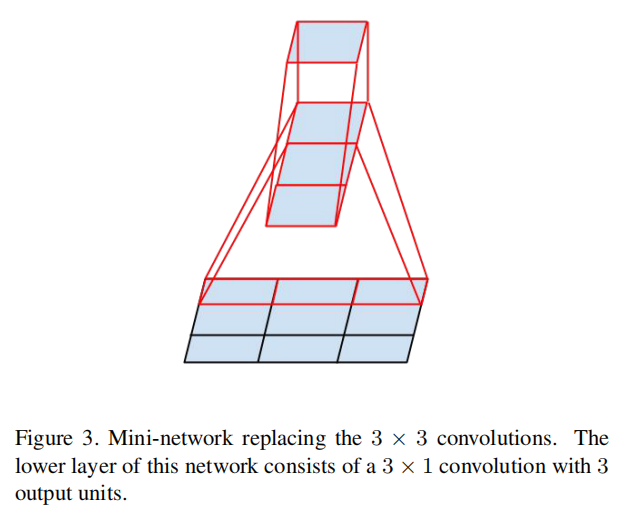
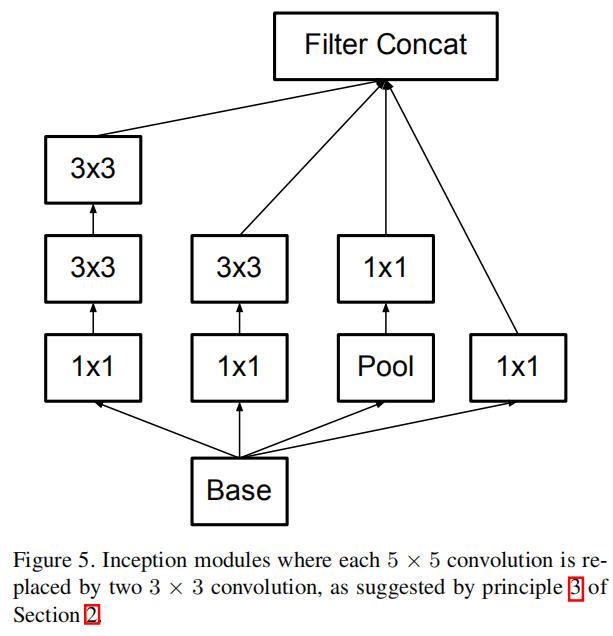
The above results suggest that convolutions with filters larger 3 × 3 a might not be generally useful as they can always be reduced into a sequence of 3 × 3 convolutional layers. Still we can ask the question whether one should factorize them into smaller, for example 2×2 convolutions. However, it turns out that one can do even better than 2 × 2 by using asymmetric convolutions, e.g. n × 1. For example using a 3 × 1 convolution followed by a 1 × 3 convolution is equivalent to sliding a two layer network with the same receptive field as in a 3 × 3 convolution (see figure 3). Still the two-layer solution is 33% cheaper for the same number of output filters, if the number of input and output filters is equal. By comparison, factorizing a 3 × 3 convolution into a two 2 × 2 convolution represents only a 11% saving of computation.
上述结果表明,滤波器大于3 × 3 的卷积通常并不有用,因为它们总是可以简化为3 × 3卷积层的序列。我们仍然可以问一个问题,是否应该把它们分解成更小的,例如2×2卷积。不过通过使用非对称卷积,例如n × 1,可以得到比2 × 2更好的结果。例如,使用3 × 1卷积和1 × 3卷积相当于滑动一个两层网络,其感受野与3 × 3卷积相同(见图3)。如果输入和输出滤波器的数量相等,对于相同数量的输出滤波器,两层解决方案仍然减少33%参数数目。相比之下,将一个3 × 3卷积分解为两个2 × 2卷积只节省了11%的计算量
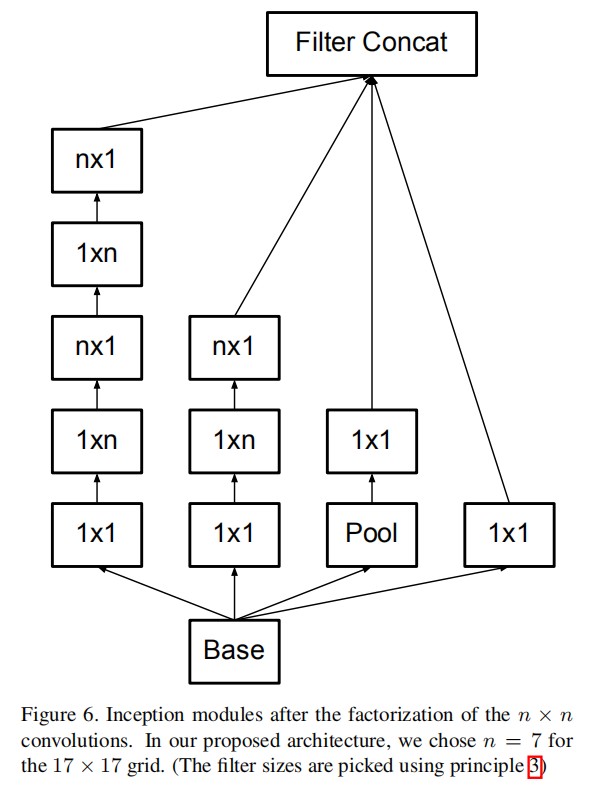
In theory, we could go even further and argue that one can replace any n × n convolution by a 1 × n convolution followed by a n × 1 convolution and the computational cost saving increases dramatically as n grows (see figure 6). In practice, we have found that employing this factorization does not work well on early layers, but it gives very good results on medium grid-sizes (On m×m feature maps, where m ranges between 12 and 20). On that level, very good results can be achieved by using 1 × 7 convolutions followed by 7 × 1 convolutions.
理论上,我们可以更进一步,认为可以用1 × n卷积,然后是n × 1卷积来代替任何n × n卷积,并且随着n的增加,计算成本节省会显著增加(见图6)。在实践中,我们发现使用这种因子分解在早期层上不能很好地工作,但是它在中等网格尺寸上给出了非常好的结果(在m×m的特征图上,其中m的范围在12和20之间)。在这个水平上,通过使用1 × 7卷积,然后是7 × 1卷积,可以获得非常好的结果
Utility of Auxiliary Classifiers
辅助分类器的效果
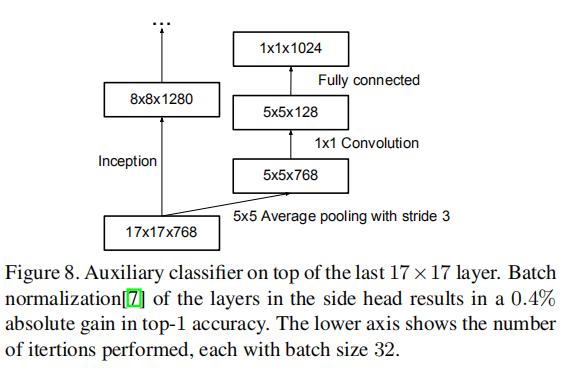
[20] has introduced the notion of auxiliary classifiers to improve the convergence of very deep networks. The original motivation was to push useful gradients to the lower layers to make them immediately useful and improve the convergence during training by combating the vanishing gradient problem in very deep networks. Also Lee et al[11] argues that auxiliary classifiers promote more stable learning and better convergence. Interestingly, we found that auxiliary classifiers did not result in improved convergence early in the training: the training progression of network with and without side head looks virtually identical before both models reach high accuracy. Near the end of training, the network with the auxiliary branches starts to overtake the accuracy of the network without any auxiliary branch and reaches a slightly higher plateau.
[20]引入了辅助分类器的概念,以改善极深网络的收敛性。最初的动机是将有用的梯度推至较低层,实现权重训练,通过在极深网络中对抗消失梯度问题来改善训练期间的收敛性。李等人[11]认为,辅助分类器促进更稳定的学习和更好的收敛。有趣的是,我们发现辅助分类器在训练的早期并没有改善收敛:在两个模型达到高精度之前,有和没有辅助分类器的网络的训练进程看起来几乎是相同的。接近训练结束时,带有辅助分支的网络开始超越没有任何辅助分支的网络的精度,并达到稍高的平台
Also [20] used two side-heads at different stages in the network. The removal of the lower auxiliary branch did not have any adverse effect on the final quality of the network. Together with the earlier observation in the previous paragraph, this means that original the hypothesis of [20] that these branches help evolving the low-level features is most likely misplaced. Instead, we argue that the auxiliary classifiers act as regularizer. This is supported by the fact that the main classifier of the network performs better if the side branch is batch-normalized [7] or has a dropout layer. This also gives a weak supporting evidence for the conjecture that batch normalization acts as a regularizer.
[20]在网络的不同阶段也使用了两个辅助分类器。移除较低的辅助分支对网络的最终质量没有任何不利影响。加上上一段中的早期观察,这意味着[20]关于这些分支有助于进化低级特征的最初假设很可能是错误的。相反,我们认为辅助分类器起着正则化的作用。支持这一点的事实是,如果辅助分支实现了批量归一化[7]或具有随机失活层,则网络的主分类器性能更好。这也为批量归一化充当正则化器的推测提供了一个弱支持证据
Efficient Grid Size Reduction
高效的网格大小(空间尺寸)缩减
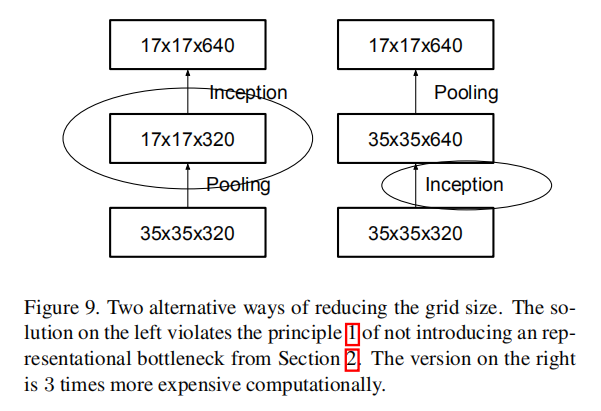
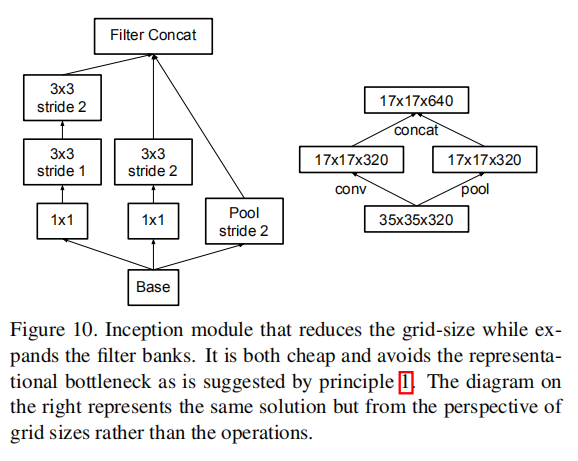
Traditionally, convolutional networks used some pooling operation to decrease the grid size of the feature maps. In order to avoid a representational bottleneck, before applying maximum or average pooling the activation dimension of the network filters is expanded. For example, starting a
grid with k filters, if we would like to arrive at a grid with filters, we first need to compute a stride-1 convolution with filters and then apply an additional pooling step. This means that the overall computational cost is dominated by the expensive convolution on the larger grid using operations. One possibility would be to switch to pooling with convolution and therefore resulting in reducing the computational cost by a quarter. However, this creates a representational bottlenecks as the overall dimensionality of the representation drops to resulting in less expressive networks (see Figure 9). Instead of doing so, we suggest another variant the reduces the computational cost even further while removing the representational bottleneck. (see Figure 10). We can use two parallel stride 2 blocks: P and C. P is a pooling layer (either average or maximum pooling) the activation, both of them are stride 2 the filter banks of which are concatenated as in figure 10.
通常情况下,卷积网络使用池化层来缩减特征图的空间尺寸(网格大小)。为了避免表示能力瓶颈,在应用最大或平均池化之前需要扩展网络滤波器的激活维度。比如,对于
Inception-v2
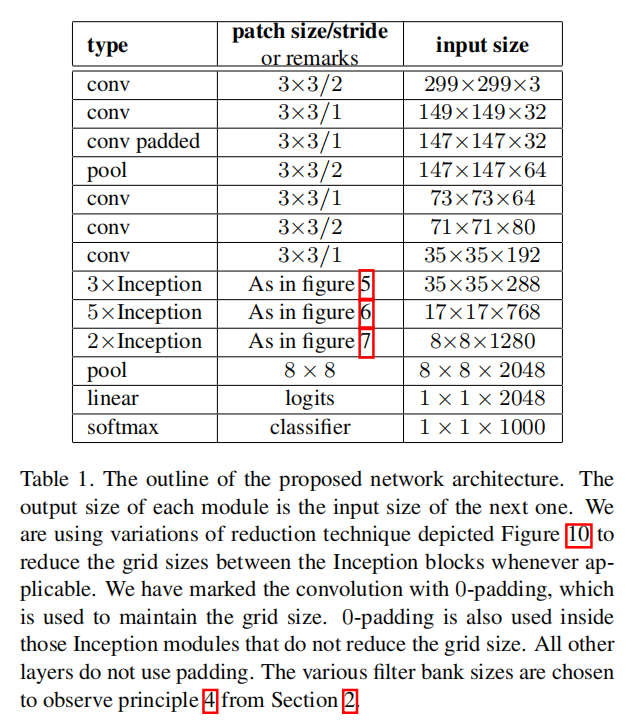
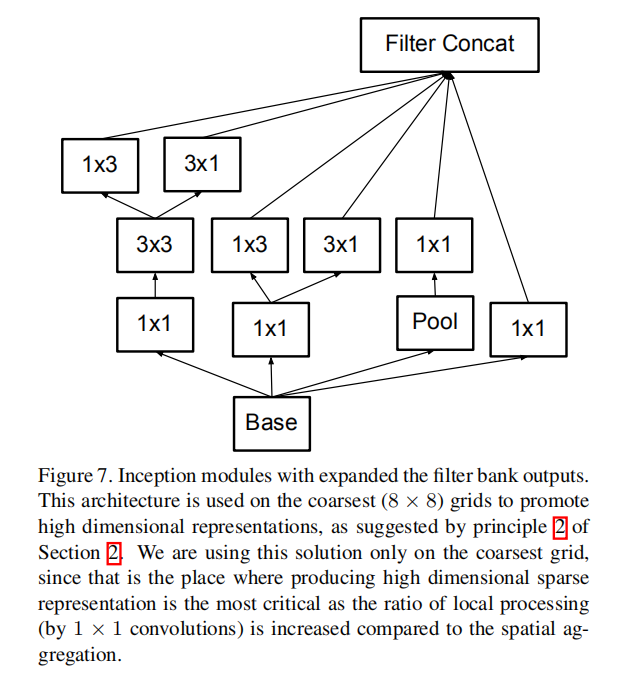
Here we are connecting the dots from above and propose a new architecture with improved performance on the ILSVRC 2012 classification benchmark. The layout of our network is given in table 1. Note that we have factorized the traditional 7 × 7 convolution into three 3 × 3 convolutions based on the same ideas as described in section 3.1. For the Inception part of the network, we have 3 traditional inception modules at the 35×35 with 288 filters each. This is reduced to a 17 × 17 grid with 768 filters using the grid reduction technique described in section 5. This is is followed by 5 instances of the factorized inception modules as depicted in figure 5. This is reduced to a 8 × 8 × 1280 grid with the grid reduction technique depicted in figure 10. At the coarsest 8 × 8 level, we have two Inception modules as depicted in figure 6, with a concatenated output filter bank size of 2048 for each tile. The detailed structure of the network, including the sizes of filter banks inside the Inception modules, is given in the supplementary material, given in the model.txt that is in the tar-file of this submission. However, we have observed that the quality of the network is relatively stable to variations as long as the principles from Section 2 are observed. Although our network is 42 layers deep, our computation cost is only about 2.5 higher than that of GoogLeNet and it is still much more efficient than VGGNet.
在这里,我们将从上面的观点联系在一起,并在ILSVRC 2012分类基准上提出一个新的具有改进性能的体系结构。我们网络的布局如表1所示。请注意,我们已经根据第3.1节中描述的相同思想,将传统的7 × 7卷积分解为三个3 × 3卷积。对于网络的Inception部分,我们在空间尺寸为35×35的时候有3个传统的Inception模块,每个模块有288个滤波器。使用第5节中描述的网格简化技术,这被简化为具有768个滤波器的17 × 17网格。接下来是5个分解的Inception模块实例,如图5所示。利用图10所示的网格简化技术,这可以简化为8 × 8 × 1280的网格。在最粗略的8 × 8级,我们有两个Inception模块,如图6所示,每个图块的级联输出滤波器组大小为2048。网络的详细结构,包括Inception模块中滤波器组的大小,在补充材料中给出,在本提交的tar文件中的model.txt中给出。然而,我们已经观察到,只要遵守第2节的原则,网络的质量对变化是相对稳定的。尽管我们的网络有42层深,但我们的计算成本仅比谷歌网络高2.5左右,而且它仍然比谷歌网络高效得多
Model Regularization via Label Smoothing
通过标签平滑进行模型正则化
Here we propose a mechanism to regularize the classifier layer by estimating the marginalized effect of label-dropout during training.
这里我们提出了一种机制,通过评估训练过程中标签丢失的边缘效应来正则化分类器
For each training example
, our model computes the probability of each label . Here, are the logits or unnormalized log-probabilities. Consider the ground-truth distribution over labels for this training example, normalized so that . For brevity, let us omit the dependence of and on example . We define the loss for the example as the cross entropy: . Minimizing this is equivalent to maximizing the expected log-likelihood of a label, where the label is selected according to its ground-truth distribution q(k). Cross-entropy loss is differentiable with respect to the logits and thus can be used for gradient training of deep models. The gradient has a rather simple form: , which is bounded between −1 and 1.
对于每个训练样本
Consider the case of a single ground-truth label
, so that and for all . In this case, minimizing the cross entropy is equivalent to maximizing the log-likelihood of the correct label. For a particular example with label , the log-likelihood is maximized for , where is Dirac delta, which equals for and otherwise. This maximum is not achievable for finite but is approached if for all – that is, if the logit corresponding to the ground-truth label is much great than all other logits. This, however, can cause two problems. First, it may result in over-fitting: if the model learns to assign full probability to the groundtruth label for each training example, it is not guaranteed to generalize. Second, it encourages the differences between the largest logit and all others to become large, and this, combined with the bounded gradient , reduces the ability of the model to adapt. Intuitively, this happens because the model becomes too confident about its predictions.
考虑一个单一的真值标签
We propose a mechanism for encouraging the model to be less confident. While this may not be desired if the goal is to maximize the log-likelihood of training labels, it does regularize the model and makes it more adaptable. The method is very simple. Consider a distribution over labels
, independent of the training example , and a smoothing parameter $$. For a training example with ground-truth label , we replace the label distribution with
我们提出一种机制来鼓励模型变得不那么自信。虽然如果目标是最大化训练标签的对数似然性,这可能不是所希望的,但是它确实正则化了模型并使其更具适应性。方法很简单。考虑基于标签的分布
which is a mixture of the original ground-truth distribution
and the fixed distribution , with weights and , respectively. This can be seen as the distribution of the label obtained as follows: first, set it to the ground-truth label ; then, with probability , replace with a sample drawn from the distribution . We propose to use the prior distribution over labels as . In our experiments, we used the uniform distribution , so that
这是一个混合了之前真值分布
We refer to this change in ground-truth label distribution as label-smoothing regularization, or LSR.
我们称这种真值标签分布的变化为标签平滑正则化,或LSR
Note that LSR achieves the desired goal of preventing the largest logit from becoming much larger than all others. Indeed, if this were to happen, then a single
would approach while all others would approach . This would result in a large cross-entropy with because, unlike , all have a positive lower bound.
请注意,LSR实现了防止最大逻辑变得比所有其他逻辑大得多的预期目标。事实上,如果发生这种情况,那么一个单一的
Another interpretation of LSR can be obtained by considering the cross entropy:
LSR的另一种解释可以由交叉熵得到:
Thus, LSR is equivalent to replacing a single cross-entropy loss
with a pair of such losses and . The second loss penalizes the deviation of predicted label distribution from the prior , with the relative weight . Note that this deviation could be equivalently captured by the KL divergence, since and is fixed. When is the uniform distribution, is a measure of how dissimilar the predicted distribution is to uniform, which could also be measured (but not equivalently) by negative entropy ; we have not experimented with this approach.
因此,LSR相当于用一对这样的损失
In our ImageNet experiments with
classes, we used and . For ILSVRC 2012, we have found a consistent improvement of about 0.2% absolute both for top-1 error and the top-5 error (cf. Table 3).
在我们对
Training Methodology
训练方法
We have trained our networks with stochastic gradient utilizing the TensorFlow [1] distributed machine learning system using 50 replicas running each on a NVidia Kepler GPU with batch size 32 for 100 epochs. Our earlier experiments used momentum [19] with a decay of 0.9, while our best models were achieved using RMSProp [21] with decay of
and . We used a learning rate of 0.045, decayed every two epoch using an exponential rate of 0.94. In addition, gradient clipping [14] with threshold 2.0 was found to be useful to stabilize the training. Model evaluations are performed using a running average of the parameters computed over time.
我们利用TensorFlow[1]分布式机器学习系统,使用随机梯度训练我们的网络,该系统使用50个副本,每个副本运行在NVidia Kepler GPU上,共100轮,批量为32。我们早期的实验使用了衰减为0.9的动量[19],而我们的最佳模型是使用衰减为0.9且
Performance on Lower Resolution Input
低分辨率输入的性能
A typical use-case of vision networks is for the the postclassification of detection, for example in the Multibox [4] context. This includes the analysis of a relative small patch of the image containing a single object with some context. The tasks is to decide whether the center part of the patch corresponds to some object and determine the class of the object if it does. The challenge is that objects tend to be relatively small and low-resolution. This raises the question of how to properly deal with lower resolution input.
视觉网络的一个典型用例是用于检测的后分类,例如在Multibox[4]环境中。这包括对包含一个具有某种背景的单一目标的图像的相对小块的分析。任务是确定patch的中心部分是否对应于某个对象,如果对应,则确定该对象的类别。挑战在于物体往往相对较小且分辨率较低。这就提出了如何正确处理低分辨率输入的问题
The common wisdom is that models employing higher resolution receptive fields tend to result in significantly improved recognition performance. However it is important to distinguish between the effect of the increased resolution of the first layer receptive field and the effects of larger model capacitance and computation. If we just change the resolution of the input without further adjustment to the model, then we end up using computationally much cheaper models to solve more difficult tasks. Of course, it is natural, that these solutions loose out already because of the reduced computational effort. In order to make an accurate assessment, the model needs to analyze vague hints in order to be able to “hallucinate” the fine details. This is computationally costly. The question remains therefore: how much does higher input resolution helps if the computational effort is kept constant. One simple way to ensure constant effort is to reduce the strides of the first two layer in the case of lower resolution input, or by simply removing the first pooling layer of the network.
普遍的看法是,采用更高分辨率感受野的模型往往会显著提高识别性能。然而,区分第一层感受野的分辨率增加的效果和较大的模型容量和计算的效果是重要的。如果我们只是改变输入的分辨率而不进一步调整模型,那么我们最终会使用计算成本低得多的模型来解决更困难的任务。当然,很自然,由于计算量的减少,这些解决方案已经失败了。为了做出准确的评估,模型需要分析模糊的暗示,以便能够“得到”精细的细节。这在计算上是昂贵的。因此,问题依然存在:如果计算量保持不变,那么更高的输入分辨率有多大帮助。确保持续有效的一个简单方法是,在低分辨率输入的情况下,减少前两层的步长,或者简单地删除网络的第一个池化层
For this purpose we have performed the following three experiments: 1.
receptive field with stride 2 and maximum pooling after the first layer. 2. receptive field with stride 1 and maximum pooling after the first layer. 3. receptive field with stride 1 and without pooling after the first layer.
为此,我们进行了以下三项实验:
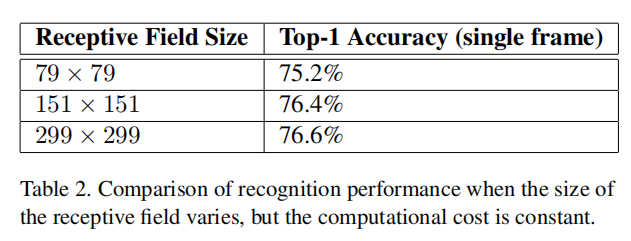
All three networks have almost identical computational cost. Although the third network is slightly cheaper, the cost of the pooling layer is marginal and (within 1% of the total cost of the)network. In each case, the networks were trained until convergence and their quality was measured on the validation set of the ImageNet ILSVRC 2012 classification benchmark. The results can be seen in table 2. Although the lower-resolution networks take longer to train, the quality of the final result is quite close to that of their higher resolution counterparts.
这三个网络的计算成本几乎相同。虽然第三个网络稍微小一点,但是池化层的成本很低(在总成本的1%以内)。在每种情况下,网络都经过训练,直到收敛,并在ImageNet ILSVRC 2012分类基准的验证集上测量其质量。结果见表2。尽管低分辨率网络需要更长的训练时间,但最终结果的质量与高分辨率网络相当接近
However, if one would just naively reduce the network size according to the input resolution, then network would perform much more poorly. However this would an unfair comparison as we would are comparing a 16 times cheaper model on a more difficult task.
然而,如果一个人只是天真地根据输入分辨率减小网络大小,那么网络的性能就会差得多。然而这将是一个不公平的比较,因为我们将在一个更困难的任务上比较一个16倍小的模型
Also these results of table 2 suggest, one might consider using dedicated high-cost low resolution networks for smaller objects in the R-CNN [5] context.
另外,表2的这些结果表明,人们可以考虑在R-CNN[5]的范围内为较小的目标使用专用的高成本低分辨率网络
Experimental Results and Comparisons
实验结果和比较
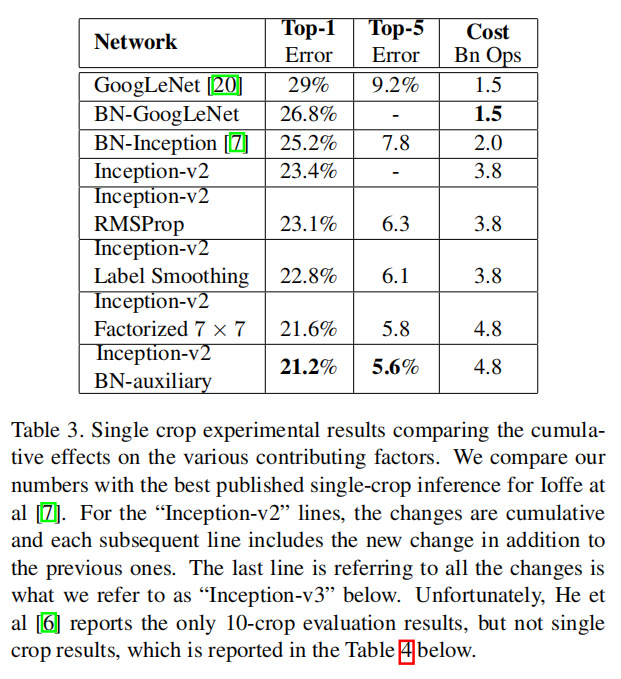
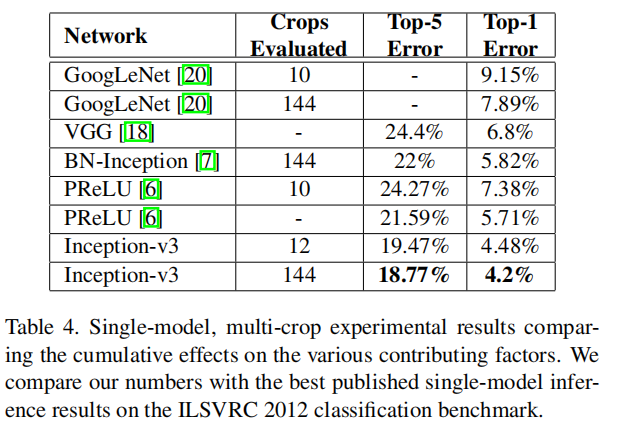
Table 3 shows the experimental results about the recognition performance of our proposed architecture (Inception-v2) as described in Section 6. Each Inception-v2 line shows the result of the cumulative changes including the highlighted new modification plus all the earlier ones. Label Smoothing refers to method described in Section 7. Factorized 7 × 7 includes a change that factorizes the first 7 × 7 convolutional layer into a sequence of 3 × 3 convolutional layers. BN-auxiliary refers to the version in which the fully connected layer of the auxiliary classifier is also batch-normalized, not just the convolutions. We are referring to the model in last row of Table 3 as Inception-v3 and evaluate its performance in the multi-crop and ensemble settings.
表3显示了第6节中描述的我们提出的架构(Inception-v2)的识别性能的实验结果。每一个Inception-v2行都显示了累积变化的结果,包括突出显示的新修改以及所有早期的修改。标签平滑是指第7节中描述的方法。分解的7 × 7包括将第一个7 × 7卷积层分解为3 × 3卷积层序列的变化。BN-辅助是指辅助分类器的全连接层也采用批量归一化实现,而不仅仅是卷积。我们将表3最后一行中的模型称为Inception-v3,并评估它在多裁剪和集成设置中的性能
All our evaluations are done on the 48238 nonblacklisted examples on the ILSVRC-2012 validation set, as suggested by [16]. We have evaluated all the 50000 examples as well and the results were roughly 0.1% worse in top-5 error and around 0.2% in top-1 error. In the upcoming version of this paper, we will verify our ensemble result on the test set, but at the time of our last evaluation of BN-Inception in spring [7] indicates that the test and validation set error tends to correlate very well.
我们所有的评估都是在ILSVRC-2012验证集的48238个nonblacklisted示例上完成的,如[16]所建议的。我们也对所有50000个样本进行了评估,结果是前5名误差大约差0.1%,前1名误差大约差0.2%。在本文的下一个版本中,我们将在测试集上验证我们的集成结果,但是在我们最后一次评估BN-Inception的时候,[7]表明测试集和验证集的误差往往关联得非常好
Conclusions
总结
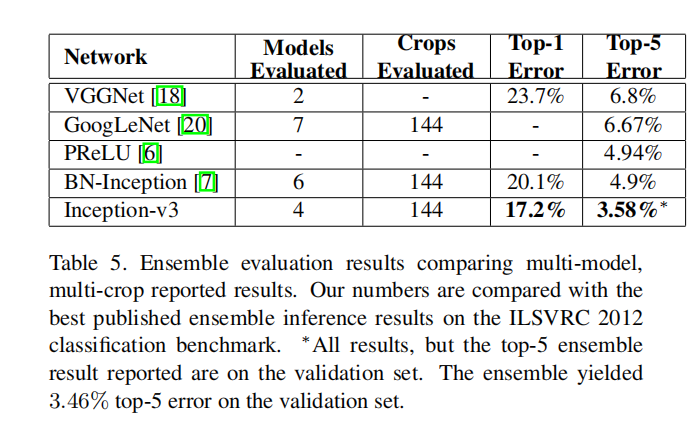
We have provided several design principles to scale up convolutional networks and studied them in the context of the Inception architecture. This guidance can lead to high performance vision networks that have a relatively modest computation cost compared to simpler, more monolithic architectures. Our highest quality version of Inception-v3 reaches 21.2%, top-1 and 5.6% top-5 error for single crop evaluation on the ILSVR 2012 classification, setting a new state of the art. This is achieved with relatively modest (2.5×) increase in computational cost compared to the network described in Ioffe et al [7]. Still our solution uses much less computation than the best published results based on denser networks: our model outperforms the results of He et al [6] – cutting the top-5 (top-1) error by 25% (14%) relative, respectively – while being six times cheaper computationally and using at least five times less parameters (estimated). Our ensemble of four Inception-v3 models reaches 3.5% with multi-crop evaluation reaches 3.5% top-5 error which represents an over 25% reduction to the best published results and is almost half of the error of ILSVRC 2014 winining GoogLeNet ensemble.
我们已经提供了几种扩大卷积网络的设计原则,并在Inception架构的背景下对它们进行了研究。与更简单、更单片化的架构相比,这种指导可以导致计算成本相对适中的高性能视觉网络。我们的Inception-v3的最高质量版本达到了21.2%,在ILSVR 2012分类的单个作物评估中,前1名和前5名误差分别为5.6%,这是一个新的技术水平。与Ioffe等人在[7]中描述的网络相比,这在计算成本上增加了相对适度(2.5倍)。然而,我们的解决方案使用的计算量比基于更密集网络的最佳公布结果少得多:我们的模型优于何等[6]的结果 - 将前5名(前1名)的误差分别减少了25% (14%)相对误差 - 同时计算成本降低了6倍,并且使用的参数(估计值)至少减少了5倍。我们的四个Inception-v3模型的集成达到了3.5%,多裁剪评估达到了3.5%的前5名误差,比最佳发布结果减少了25%以上,几乎是ILSVRC 2014 冠军GoogLeNet集成误差的一半
We have also demonstrated that high quality results can be reached with receptive field resolution as low as 79×79. This might prove to be helpful in systems for detecting relatively small objects. We have studied how factorizing convolutions and aggressive dimension reductions inside neural network can result in networks with relatively low computational cost while maintaining high quality. The combination of lower parameter count and additional regularization with batch-normalized auxiliary classifiers and label-smoothing allows for training high quality networks on relatively modest sized training sets.
我们还证明了在感受野分辨率低至79×79的情况下可以获得高质量的结果。这可能对探测相对较小物体的系统有所帮助。我们已经研究了神经网络内部的因子分解卷积和积极的降维如何能够在保持高质量的同时产生具有相对低的计算成本的网络。低参数总数和附加正则化与批量归一化辅助分类器和标签平滑的结合允许在相对适中的训练集上训练高质量的网络
Gitalk 加载中 ...