GoogLeNet_BN
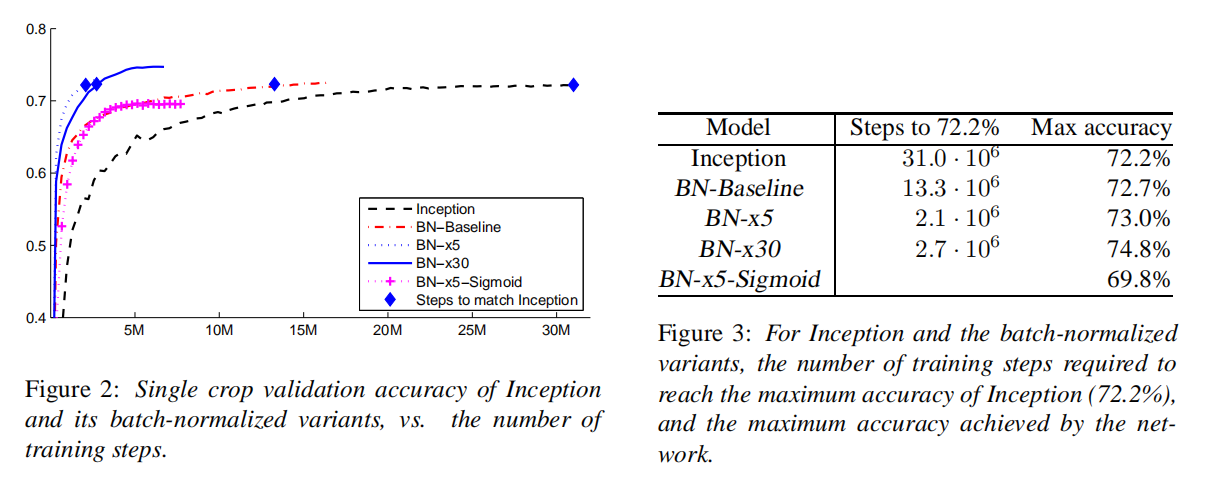
论文Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift将批量归一化方法作用于卷积神经网络,通过校正每层输入数据的数据分布,从而达到更快的训练目的。在文章最后,添加批量归一化层到GoogLeNet网络,得到了更好的检测效果
参数解析
论文中以表格方式给出了GoogLeNet_BN的参数设置
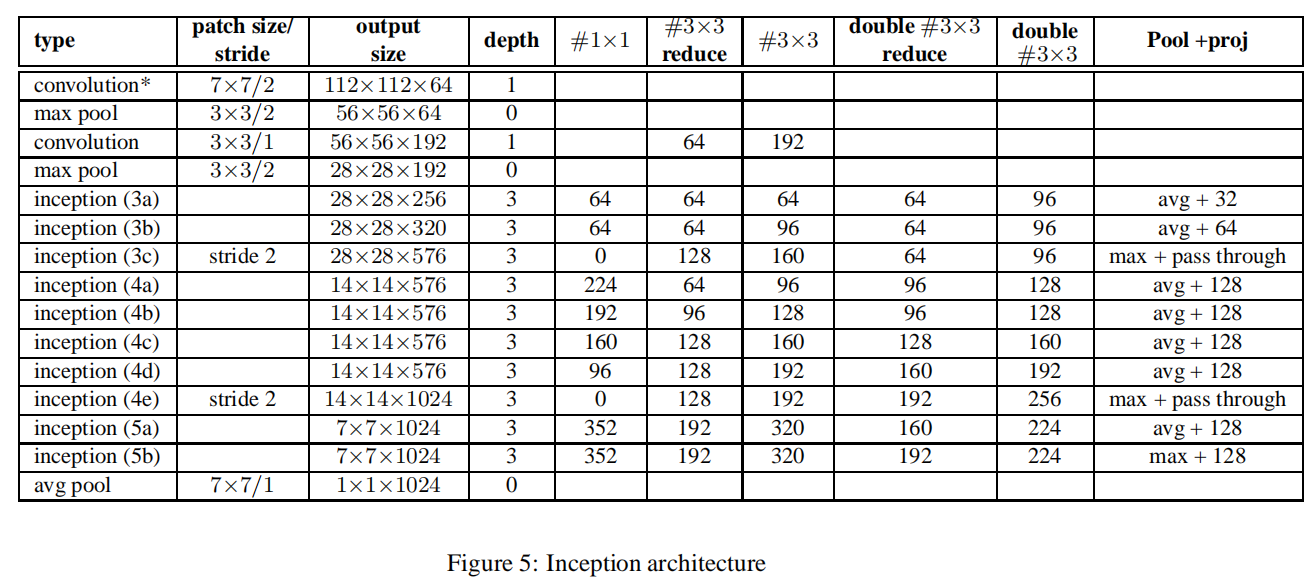
其相对于GoogLeNet的修改如下:
- 在
Inception模块中,9个权重层,从而使得参数数量提高了25%,计算耗时增加了30% - 增加了
Inception (3c) - 在
Inception模块中,使用平均池化(average pooling)或者最大池化(max pooling) - 在各个
Inception模块之间不再使用池化层进行操作,而是在Inception 3c/4e模块中使用步长2进行减半操作
同时GoogLeNet_BN在第一个卷积层使用了深度乘数为8的可分离卷积,以此来加速计算
Our model employed separable convolution with depth multiplier 8 on the first convolutional layer. This reduces the computational cost while increasing the memory consumption at training time
Note:经过计算后发现,Inception (4c/d/e)的输出深度有错误,应该分别为
推导
以Inception 3(a/b/c)模块为例,尝试推导修改后的模块实现
假定输入大小为
Inception (3a)
1x1
- 输入数据体:
- 卷积核大小为
- 滤波器个数:
- 输出数据体:
3x3
先执行
- 输入数据体:
- 卷积核大小为
- 滤波器个数:
- 输出数据体:
再执行
- 输入数据体:
- 卷积核大小为
- 滤波器个数:
- 输出数据体:
double 3x3
先执行
- 输入数据体:
- 卷积核大小为
- 滤波器个数:
- 输出数据体:
第一次执行
- 输入数据体:
- 卷积核大小为
- 滤波器个数:
- 输出数据体:
第二次执行
- 输入数据体:
- 卷积核大小为
- 滤波器个数:
- 输出数据体:
avg pooling
先执行
- 输入数据体:
- 卷积核大小为
- 输出数据体:
再执行
- 输入数据体:
- 卷积核大小为
- 滤波器个数:
- 输出数据体:
连接
上述4个子模块计算得到了相同的空间尺寸的输出书具体,然后按深度通道进行连接,最后得到
Inception (3b)
1x1
- 输入数据体:
- 卷积核大小为
- 滤波器个数:
- 输出数据体:
3x3
先执行
- 输入数据体:
- 卷积核大小为
- 滤波器个数:
- 输出数据体:
再执行
- 输入数据体:
- 卷积核大小为
- 滤波器个数:
- 输出数据体:
double 3x3
先执行
- 输入数据体:
- 卷积核大小为
- 滤波器个数:
- 输出数据体:
第一次执行
- 输入数据体:
- 卷积核大小为
- 滤波器个数:
- 输出数据体:
第二次执行
- 输入数据体:
- 卷积核大小为
- 滤波器个数:
- 输出数据体:
avg pooling
先执行
- 输入数据体:
- 卷积核大小为
- 输出数据体:
再执行
- 输入数据体:
- 卷积核大小为
- 滤波器个数:
- 输出数据体:
连接
上述4个子模块计算得到了相同的空间尺寸的输出书具体,然后按深度通道进行连接,最后得到
Inception (3c)
其步长为
3x3
先执行
- 输入数据体:
- 卷积核大小为
- 滤波器个数:
- 输出数据体:
再执行
- 输入数据体:
- 卷积核大小为
- 滤波器个数:
- 输出数据体:
double 3x3
先执行
- 输入数据体:
- 卷积核大小为
- 滤波器个数:
- 输出数据体:
第一次执行
- 输入数据体:
- 卷积核大小为
- 滤波器个数:
- 输出数据体:
第二次执行
- 输入数据体:
- 卷积核大小为
- 滤波器个数:
- 输出数据体:
max pooling
先执行
- 输入数据体:
- 卷积核大小为
- 输出数据体:
连接
上述4个子模块计算得到了相同的空间尺寸的输出数据,然后按深度通道进行连接,最后得到stride=2的目的,抑或者是参数表的错误。当前具体实现中不使用stride=2进行减半,还是通过Max Pooling)
PyTorch
关于
GoogLeNet实现参考:GoogLeNet关于
GoogLeNet_BN的具体实现参考:zjZSTU/GoogLeNet
BasicConv2d
在卷积操作后执行批量归一化
1 | class BasicConv2d(nn.Module): |
Inception
- 修改
- 根据输入选择最大池化或者平均池化操作
1 | class Inception(nn.Module): |
GoogLeNet_BN
1 | class GoogLeNet_BN(nn.Module): |
测试
比较GoogLeNet_BN与GoogLeNet.具体测试代码参考test_googlenet_bn.py
参数个数
1 | [googlenet_bn] param num: 17683640 |
GoogLeNet有1768万个参数,GoogLeNet有1337万个,两者相差1.32倍
测试时间
1 | [googlenet_bn] time: 0.0596 |
计算100次测试图像平均使用时间:
GoogLeNet_BN:0.0596秒GoogLeNet:0.0602秒
两者的计算时间相近
训练
比对GoogLeNet_BN和GoogLeNet训练,训练参数如下:
- 数据集:
PASCAL VOC 07+12,20类共40058个训练样本和12032个测试样本 - 批量大小:
128 - 优化器:
Adam,学习率为1e-3 - 随步长衰减:每隔
8轮衰减4%,学习因子为0.96 - 迭代次数:
100轮
训练100次结果如下:
1 | {'train': 40058, 'test': 12032} |
100轮迭代后,GoogLeNet_BN实现了74.78%的最好测试精度;GoogLeNet实现了74.23%的最好测试精度
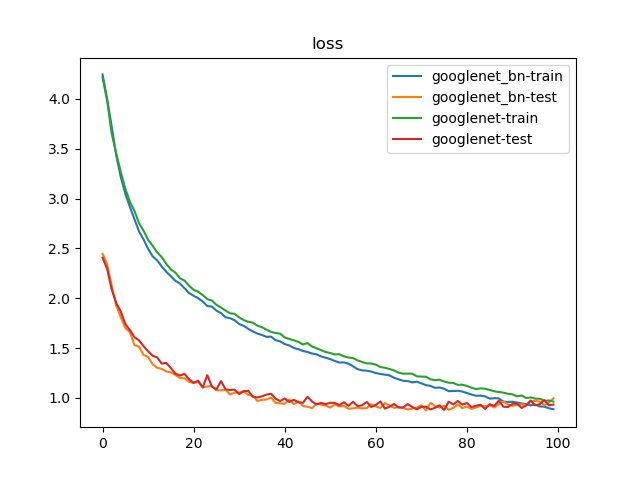
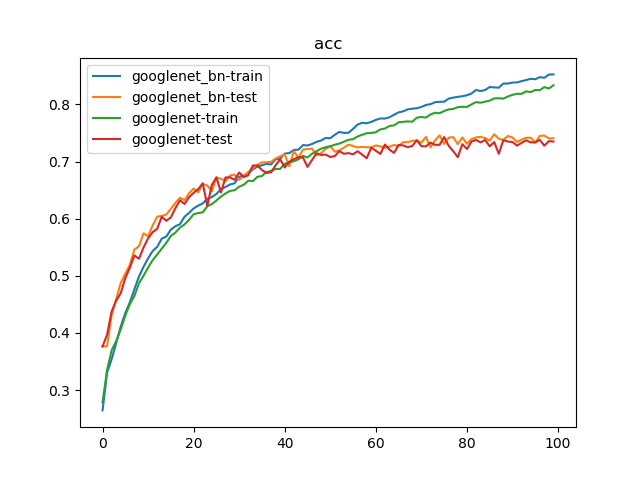
未找到相关的 Issues 进行评论
请联系 @zjykzj 初始化创建