激活函数

发表于 2019-04-30 更新于 2021-04-14 分类于深度学习/deeplearning 阅读次数：

本文字数： 2.4k 阅读时长 ≈ 4 分钟

介绍激活函数及其特性

Sigmoid
Tanh
ReLU
Leaky ReLU
Maxout

`Sigmoid`

Sigmoid函数是最早出现的激活函数，估计是因为逻辑回归模型的缘故

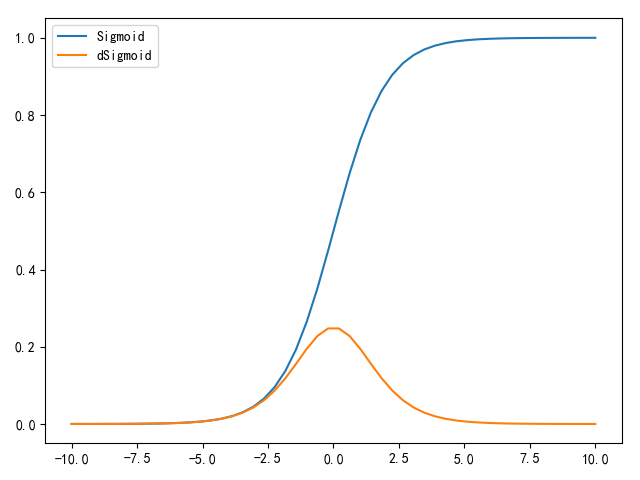
它能够将输入数据压缩到[0,1]之间，值越小，越接近于0；值越大，越接近于1。数学公式如下：

\[ \sigma (x)=\frac{1}{1+e^{-x}} \]

\[ \frac {\varphi \sigma (x)}{\varphi x}= \frac{-1}{(1+e^{-x})^2}\cdot e^{-x} \cdot (-1)= \frac{1}{1+e^{-x}}\cdot \frac{e^{-x}}{1+e^{-x}}= \sigma (x)\cdot (1-\sigma (x)) \]

目前基本不使用Sigmoid作为激活函数，主要有两个缺陷

当激活值处于饱和（saturate）状态（接近0或1），此时得到的梯度几乎为0（如下图所示），也就是说无法在反向传播过程中对权重进行有效更新，网络也将停止学习。所以初始化权重值不能过大，否则会导致激活函数饱和
因为Sigmoid的取值范围是[0,1]，所以其输出不是零中心（zero-centered）。如果输入的数据总是正值，会导致计算得到的梯度值变为全正或全负（依赖于线性运算的表达式\(f\)）。非零中心会导致权重更新时呈\(Z\)字形下降，这个问题可以通过初始化权重时平衡正负值来减轻影响

def sigmoid(x):
    return 1.0 / (1 + np.exp(-1 * x))

def dsigmoid(x):
    return sigmoid(x) * (1 - sigmoid(x))

`Tanh`

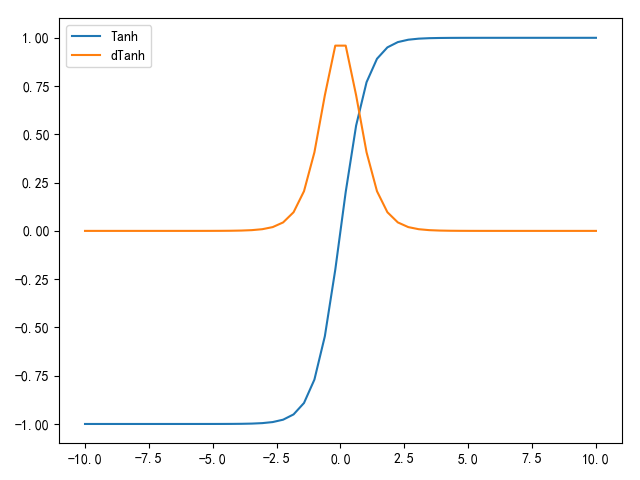
Tanh（全局正切）函数在Sigmoid函数的基础上进一步发展，其将取值压缩在[-1,1]之间，值越小，越接近于-1；值越大，越接近于1。数学公式如下：

\[ tanh(x) = \frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}=\frac{1-e^{-2x}}{1+e^{-2x}}=\frac{2-(1+e^{-2x})}{1+e^{-2x}}=2\sigma (2x)+1 \]

\[ \frac {\varphi tanh(x)}{\varphi x}= \frac {v(x)'\cdot u(x)-v(x)\cdot u(x)'}{u(x)^2} \]

其中

\[ v(x)=e^{x}-e^{-x} \Rightarrow {v(x)}'= e^{x}+e^{-x} \\ u(x)=e^{x}+e^{-x} \Rightarrow {u(x)}'= e^{x}-e^{-x} \]

所以

\[ \frac {\varphi tanh(x)}{\varphi x}=\frac {u(x)^2-v(x)^2}{u(x)^2}= 1-(tanh(x))^2 \]

根据公式可知，\(tanh\)函数是\(sigmoid\)函数的扩展，它解决了输出零中心的问题

def tanh(x):
    x1 = np.exp(x)
    x2 = np.exp(-1 * x)
    return (x1 - x2) / (x1 + x2)
    # return 2 * sigmoid(2 * x) + 1

def dtanh(x):
    return 1 - tanh(x) ** 2

`ReLU`

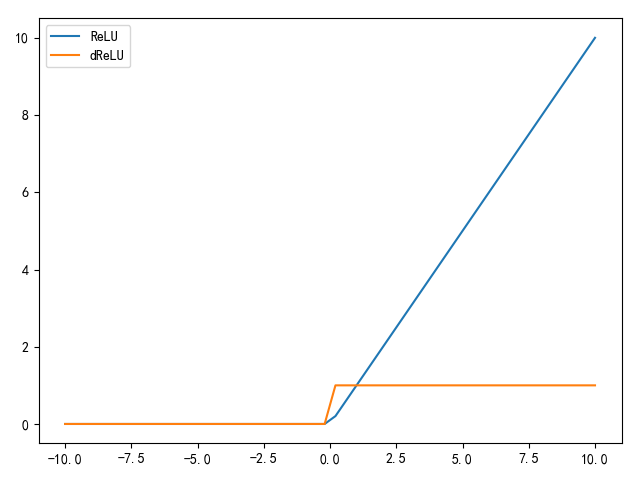
ReLU(Rectified Linear Unit，整流线性单元)激活函数是因为在AlexNet网络中的使用而得到了推广。当输入小于0时，输出为0；否则，输入为输出值。其数学公式如下：

\[ f(x)=\max (0,x) \]

\[ \frac {\varphi f(x)}{\varphi x}= \left\{\begin{matrix} 0, x<0\\ 1, x\geq 0 \end{matrix}\right. =1(x\geq 0) \]

优势如下：

计算高效。达到同样训练误差率的时间，使用ReLU能够比tanh快6倍
实现简单。相比于sigmoid/tanh需要指数运算，ReLU仅是线性阈值操作

缺陷如下：

输出值没有零中心
当输入值小于0时，梯度消失，权值不再更新

如果步长（learning rate，学习率）设置过大，有可能导致梯度更新后，神经元线性计算结果永远小于0，无法再次更新权值，也就是说这个神经元在训练过程中死亡了，所以需要合理设置步长大小

def relu(x):
    return np.array(list(map(lambda x: x if x > 0 else 0, x)))

def drelu(x):
    return x >= 0

`Leaky ReLU`

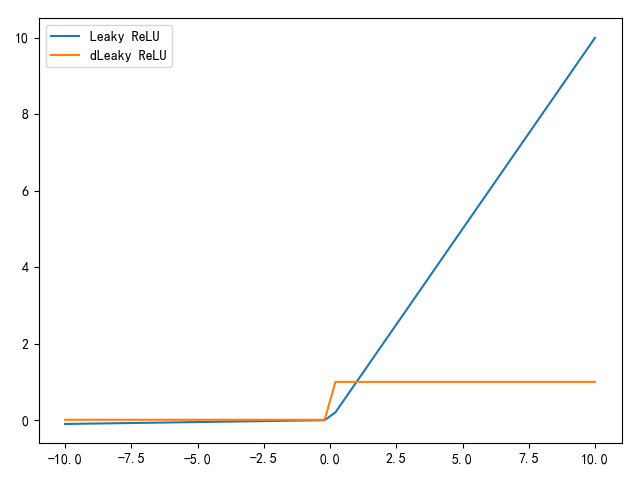
Leaky ReLU试图解决ReLU单侧梯度消失的问题，其实现公式如下：

\[ f(x)=I (x<0)(ax)+I (x>=0)(x) \]

\[ \frac {\varphi f(x)}{\varphi x}= \left\{\begin{matrix} a, x<0\\ 1, x\geq 0 \end{matrix}\right. \]

其中\(a\)是一个超参数，通常是一个很小的常数（比如\(0.01\)），这样当输入值小于\(0\)时仍旧能够进行权重更新

def leaky_relu(x, a=0.01):
    return np.array(list(map(lambda x: x if x > 0 else a * x, x)))

def dleaky_relu(x, a=0.01):
    return np.array(list(map(lambda x: 1 if x > 0 else a, x)))

小结

推荐使用顺序：ReLU > Leaky ReLU > Tanh > Sigmoid

大海

激活函数

`Sigmoid`

`Tanh`

`ReLU`

`Leaky ReLU`

小结

相关阅读