神经网络推导-单个数据

发表于 2019-05-01 更新于 2021-04-04 分类于算法，深度学习，数学阅读次数：

本文字数： 16k 阅读时长 ≈ 30 分钟

参考：

神经网络概述

神经网络

输入单个数据到神经网络，进行前向传播和反向传播的推导

预备知识

链式法则
雅可比矩阵

链式法则

参考：链式法则

反向传播（backpropagatation）的目的是进行可学习参数（learnable parameters）的更新，其实现方式是利用链式法则（chain rule）进行梯度计算

cs231n的Backpropagation, Intuitions 给出了生动的关于链式求导的学习示例

简单函数求导

对于简单函数而言，其导数计算方式很简单。比如

$$
f(x,y)=x\pm y \Rightarrow \frac{d f}{d x}=1 \ \ \frac{d f}{d y}=\pm 1 \
f(x)=ax \Rightarrow \frac{d f}{d x}=a \
f(x)=\frac {1}{x} \Rightarrow \frac{d f}{d x}=\frac {-1}{x^2} \
f(x)=e^{x} \Rightarrow \frac{d f}{d x}=e^{x} \
f(x,y)=max(x,y) \Rightarrow \frac{d f}{d x}=\mathbb{1}(x>=y) \ \ \frac{d f}{d y}=\mathbb{1}(y>=x)
$$

复合函数求导

对于复合函数而言，直接计算导数很复杂，但它可以拆分为多个简单函数，然后逐一进行计算

以函数$f(x_{1},x_{2})$为例，其实现公式如下：

$$
f(x_{1},x_{2})=\frac{1}{1+e^{-(w_{0}+w_{1}\cdot x_{1}+w_{2}\cdot x_{2})}}
$$

其中函数可拆分成如下形式：

$$
\sigma (x)=\frac {1}{1+e^{-x}} \
p(x)= w\cdot x\
$$

对$\sigma (x)$和$p(x)$求导如下：

$$
\frac{d \sigma}{d x} = \frac {-1}{(1+e^{-x})^2}\cdot (-e^{-x}) = \sigma (x)(1-\sigma (x)) \
\frac{d p}{d x} = w
$$

所以函数$f(x_{1},x_{2})$求导如下：

$$
\frac{d f}{d x_{1}}=\frac{d \sigma}{d p}\cdot \frac{d p}{d x_{1}}=f(x_{1},x_{2})\cdot (1-f(x_{1},x_{2}))\cdot w_{1} \
\frac{d f}{d x_{2}}=\frac{d \sigma}{d p}\cdot \frac{d p}{d x_{2}}=f (x_{1},x_{2})\cdot (1-f (x_{1},x_{2}))\cdot w_{2}
$$

可以用相同的方式对权重$w_{1},w_{2}$求导

所以链式法则指的是将复合函数拆分为一个个简单函数，通过组合简单函数的导数得到复合函数的导数，最后组成梯度进行权值更新

雅可比矩阵

假设函数从$R^{n}$映射到$R^{m}$，其雅可比（Jacobian）矩阵就是从$R^{n}$到$R^{m}$的线性映射

如果函数由$m$个实函数组成：$y_{1}(x_{1},…,x_{n}),…,y_{m}(x_{1},…,x_{n})$，则其偏导数（如果存在）可以组成一个$m$行$n$列的雅可比矩阵

$$
\left[ \begin{array}{ccc}{\frac{\partial y_{1}}{\partial x_{1}}} & {\cdots} & {\frac{\partial y_{1}}{\partial x_{n}}} \ {\vdots} & {\ddots} & {\vdots} \ {\frac{\partial y_{m}}{\partial x_{1}}} & {\cdots} & {\frac{\partial y_{m}}{\partial x_{n}}}\end{array}\right]
$$

其大小为$m\times n$

在神经网络中每次计算的输入输出结果都是向量或矩阵，所以其偏导数均可以组成Jacobian矩阵

比如函数$f’(z^{l})$表示输出向量$a^{(l)}$对输入向量$z^{(l)}$求导，就是一个雅可比矩阵

$$
\left[ \begin{array}{ccc}{\frac{\partial a^{(l)}{1}}{\partial z^{(l)}{1}}} & {\cdots} & {\frac{\partial a^{(1)}{1}}{\partial z^{(l)}{n}}} \ {\vdots} & {\ddots} & {\vdots} \ {\frac{\partial a^{(l)}{m}}{\partial z^{(l)}{1}}} & {\cdots} & {\frac{\partial a^{(l)}{m}}{\partial z^{(l)}{n}}}\end{array}\right]
$$

其大小为$n^{(l)}\times n^{(l)}$

网络符号定义

规范神经网络的计算符号

关于神经元和层数

$L$表示网络层数（不计入输入层）
- $L=2$，其中输入层是第0层，隐藏层是第1层，输出层是第2层
$n^{(l)}$表示第$l$层的神经元个数（不包括偏置神经元）
- $n^{(0)}=3$，表示输入层神经元个数为3
- $n^{(1)}=4$，表示隐藏层神经元个数为4
- $n^{(2)}=2$，表示输出层神经元个数为2

关于权重矩阵和偏置值

$W^{(l)}$表示第$l-1$层到第$l$层的权重矩阵，矩阵行数为第$l$层的神经元个数，列数为第$l-1$层神经元个数
- $W^{(1)}$表示输入层到隐藏层的权重矩阵，大小为$R^{4\times 3}$
- $W^{(2)}$表示隐藏层到输出层的权重矩阵，大小为$R^{2\times 4}$
$W^{(l)}_{i,j}$表示第$l$层第$i$个神经元到第$l-1$第$j$个神经元的权值
- $i$的取值范围是$[1,n^{(l)}]$
- $j$的取值范围是$[1, n^{(l-1)}]$
$W^{(l)}_{i}$表示第$l$层第$i$个神经元对应的权重向量，大小为$n^{(l-1)}$
$W^{(l)}_{,j}$表示第$l-1$层第$j$个神经元对应的权重向量，大小为$n^{(l)}$
$b^{(l)}$表示第$l$层的偏置向量
- $b^{(1)}$表示输入层到隐藏层的偏置向量，大小为$R^{4\times 1}$
- $b^{(2)}$表示隐藏层到输出层的偏置向量，大小为$R^{2\times 1}$
$b^{(l)}_{i}$表示第$l$层第$i$个神经元的偏置值
- $b^{(1)}_{2}$表示第$1$层隐藏层第$2$个神经元的偏置值

关于神经元输入向量和输出向量

$a^{(l)}$表示第$l$层输出向量，$a^{(l)}=[a^{(l)}{1},a^{(l)}{2},…,a^{(l)}_{n^{l}}]^{T}$
- $a^{(0)}$表示输入层输出向量，大小为$R^{3\times 1}$
- $a^{(1)}$表示隐藏层输出向量，大小为$R^{4\times 1}$
- $a^{(2)}$表示输出层输出向量，大小为$R^{2\times 1}$
$a^{(l)}_{i}$表示第$l$层第$i$个单元的输出值，其是输入向量经过激活计算后的值
- $a^{(1)}{3}$表示隐含层第$3$个神经元的输入值，$a^{(1)}{3}=g(z^{(1)}_{3})$
$z^{(l)}$表示第$l$层输入向量，$z^{(l)}=[z^{(l)}{1},z^{(l)}{2},…,z^{(l)}_{n^{l}}]^{T}$
- $z^{(1)}$表示隐藏层的输入向量，大小为$R^{4\times 1}$
- $z^{(2)}$表示输出层的输入向量，大小为$R^{2\times 1}$
$z^{(l)}_{i}$表示第$l$层第$i$个单元的输入值，其是上一层输出向量和该层第$i$个神经元权重向量的加权累加和
- $z^{(1)}{1}$表示隐藏层第$1$个神经元的输入值，$z^{(1)}{1}=b^{(1)}{1}+W^{(1)}{1,1}\cdot a^{(0)}{1}+W^{(1)}{1,2}\cdot a^{(0)}{2}+W^{(1)}{1,3}\cdot a^{(0)}_{3}$

关于神经元激活函数

$g()$表示激活函数操作

关于评分函数和损失函数

$h()$表示评分函数操作
$J()$表示代价函数操作

神经元执行步骤

神经元操作分为2步计算：

输入向量$z^{(l)}$=前一层神经元输出向量$a^{(l-1)}$与权重矩阵$W^{(l)}$的加权累加和+偏置向量

$$
z^{(l)}{j}=W^{(l)}{i,j}\cdot a^{(l-1)}{i} + b^{(l)}{j} \Rightarrow
z^{(l)}=W^{(l)}\cdot a^{(l-1)} + b^{(l)}
$$

输出向量$a^{(l)}$=对输入向量$z^{(l)}$进行激活函数操作

$$
a^{(l)}{i}=g(z{i}^{(l)})
\Rightarrow
a^{(l)}=g(z^{(l)})
$$

TestNet网络

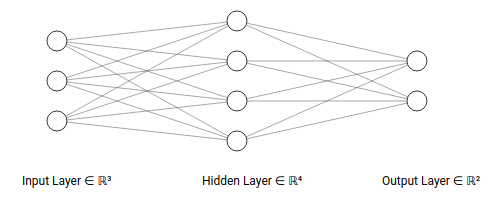
TestNet是一个2层神经网络，结构如下：

输入层有3个神经元
隐藏层有4个神经元
输出层有2个神经元

激活函数为relu函数
评分函数为softmax回归
代价函数为交叉熵损失

对输入层

$$
a^{(0)}=
\begin{bmatrix}
a^{(0)}{1}\
a^{(0)}{2}\
a^{(0)}_{3}
\end{bmatrix}
\in R^{3\times 1}
$$

对隐藏层

$$
W^{(1)}
=\begin{bmatrix}
W^{(1)}{1,1} & W^{(1)}{1,2} & W^{(1)}{1,3}\
W^{(1)}{2,1} & W^{(1)}{2,2} & W^{(1)}{2,3}\
W^{(1)}{3,1} & W^{(1)}{3,2} & W^{(1)}{3,3}\
W^{(1)}{4,1} & W^{(1)}{4,2} & W^{(1)}{4,3}
\end{bmatrix}
\in R^{4\times 3}
$$

$$
b^{(1)}=
\begin{bmatrix}
b^{(1)}{1}\
b^{(1)}{2}\
b^{(1)}{3}\
b^{(1)}{4}
\end{bmatrix}
\in R^{4\times 1}
$$

$$
z^{(1)}=
\begin{bmatrix}
z^{(1)}{1}\
z^{(1)}{2}\
z^{(1)}{3}\
z^{(1)}{4}
\end{bmatrix}
\in R^{4\times 1}
$$

$$
a^{(1)}=
\begin{bmatrix}
a^{(1)}{1}\
a^{(1)}{2}\
a^{(1)}{3}\
a^{(1)}{4}
\end{bmatrix}
\in R^{4\times 1}
$$

对输出层

$$
W^{(2)}
=\begin{bmatrix}
W^{(2)}{1,1} & W^{(2)}{1,2} & W^{(2)}{1,3} & W^{(2)}{1,4}\
W^{(2)}{2,1} & W^{(2)}{2,2} & W^{(2)}{2,3} & W^{(2)}{2,4}
\end{bmatrix}
\in R^{2\times 4}
$$

$$
b^{(2)}=
\begin{bmatrix}
b^{(2)}{1}\
b^{(2)}{2}
\end{bmatrix}
\in R^{4\times 1}
$$

$$
z^{(2)}=
\begin{bmatrix}
z^{(2)}{1}\
z^{(2)}{2}
\end{bmatrix}
\in R^{4\times 1}
$$

评分值

$$
h(z^{(2)})
=\begin{bmatrix}
p(y=1)\
p(y=2)
\end{bmatrix}
\in R^{2\times 1}
$$

损失值

$$
J(z^{(2)})=(-1)\cdot 1(y=1)\ln p(y=1)+(-1)\cdot 1(y=2)\ln p(y=2)\in R^{1}
$$

前向传播

对于输入层神经元，其得到输入数据后直接输出到下一层，并没有进行权值操作和激活函数操作，所以严格意义上讲输入层不是真正的神经元
对于输出层神经元，其得到输入数据，进行加权求和后直接输出进行评分函数计算，没有进行激活函数操作

输入层到隐藏层计算

$$
z^{(1)}{1}=W^{(1)}{1}\cdot a^{(0)}+b^{(1)}{1}
=W^{(1)}{1,1}\cdot a^{(0)}{1}
+W^{(1)}{1,2}\cdot a^{(0)}{2}
+W^{(1)}{1,3}\cdot a^{(0)}{3}
+b^{(1)}{1}
$$

$$
z^{(1)}{2}=W^{(1)}{2}\cdot a^{(0)}+b^{(1)}{2}
=W^{(1)}{2,1}\cdot a^{(0)}{1}
+W^{(1)}{2,2}\cdot a^{(0)}{2}
+W^{(1)}{2,3}\cdot a^{(0)}{3}
+b^{(1)}{2}
$$

$$
z^{(1)}{3}=W^{(1)}{3}\cdot a^{(0)}+b^{(1)}{3}
=W^{(1)}{3,1}\cdot a^{(0)}{1}
+W^{(1)}{3,2}\cdot a^{(0)}{2}
+W^{(1)}{3,3}\cdot a^{(0)}{3}
+b^{(1)}{3}
$$

$$
z^{(1)}{4}=W^{(1)}{4}\cdot a^{(0)}+b^{(1)}{4}
=W^{(1)}{4,1}\cdot a^{(0)}{1}
+W^{(1)}{4,2}\cdot a^{(0)}{2}
+W^{(1)}{4,3}\cdot a^{(0)}{3}
+b^{(1)}{4}
$$

$$
\Rightarrow z^{(1)}
=[z^{(1)}{1},z^{(1)}{2},z^{(1)}{3},z^{(1)}{4}]^{T}
=W^{(1)}\cdot a^{(0)}+b^{(1)}
$$

隐藏层输入向量到输出向量

$$
a^{(1)}{1}=relu(z^{(1)}{1}) \
a^{(1)}{2}=relu(z^{(1)}{2}) \
a^{(1)}{3}=relu(z^{(1)}{3}) \
a^{(1)}{4}=relu(z^{(1)}{4})
$$

$$
\Rightarrow
a^{(1)}=[a^{(1)}{1},a^{(1)}{2},a^{(1)}{3},a^{(1)}{4}]^{T}
=relu(z^{(1)})
$$

隐藏层到输出层计算

$$
z^{(2)}{1}=W^{(2)}{1}\cdot a^{(1)}+b^{(2)}{1}
=W^{(2)}{1,1}\cdot a^{(1)}{1}
+W^{(2)}{1,2}\cdot a^{(1)}{2}
+W^{(2)}{1,3}\cdot a^{(1)}{3}
+W^{(2)}{1,4}\cdot a^{(1)}{4}
+b^{(2)}{1}
$$

$$
z^{(2)}{2}=W^{(2)}{2}\cdot a^{(1)}+b^{(2)}{2}
=W^{(2)}{2,1}\cdot a^{(1)}{1}
+W^{(2)}{2,2}\cdot a^{(1)}{2}
+W^{(2)}{2,3}\cdot a^{(1)}{3}
+W^{(2)}{2,4}\cdot a^{(1)}{4}
+b^{(2)}{2}
$$

$$
\Rightarrow z^{(2)}
=[z^{(2)}{1},z^{(2)}{2}]^{T}
=W^{(2)}\cdot a^{(1)}+b^{(2)}
$$

评分操作

$$
p(y=1)=\frac {exp(z^{(2)}{1})}{\sum exp(z^{(2)})} \ \
p(y=2)=\frac {exp(z^{(2)}{2})}{\sum exp(z^{(2)})}
$$

$$
\Rightarrow h(z^{(2)})
=[p(y=1),p(y=2)]^{T}
=[\frac {exp(z^{(2)}{1})}{\sum exp(z^{(2)})}, \frac {exp(z^{(2)}{2})}{\sum exp(z^{(2)})}]^{T}
$$

损失值

$$
J(z^{(2)})=(-1)\cdot 1(y=1)\ln p(y=1)+(-1)\cdot 1(y=2)\ln p(y=2)
$$

反向传播

计算输出层输入向量梯度

$$
\frac {\partial J}{\partial z^{(2)}{1}}=
(-1)\cdot \frac {1(y=1)}{p(y=1)}\cdot \frac {\partial p(y=1)}{\partial z^{(2)}{1}}
+(-1)\cdot \frac {1(y=2)}{p(y=2)}\cdot \frac {\partial p(y=2)}{\partial z^{(2)}_{1}}
$$

$$
\frac {\partial p(y=1)}{\partial z^{(2)}{1}}
=\frac {exp(z^{(2)}{1})\cdot \sum exp(z^{(2)})-exp(z^{(2)}{1})\cdot exp(z^{(2)}{1})}{(\sum exp(z^{(2)}))^{2}}
=\frac {exp(z^{(2)}{1})}{\sum exp(z^{(2)})}
-(\frac {exp(z^{(2)}{1})}{\sum exp(z^{(2)})})^2
=p(y=1)-(p(y=1))^2
$$

$$
\frac {\partial p(y=2)}{\partial z^{(2)}{1}}
=\frac {-exp(z^{(2)}{2})\cdot exp(z^{(2)}{1})}{(\sum exp(z^{(2)}))^2}
=(-1)\cdot \frac {exp(z^{(2)}{1})}{\sum exp(z^{(2)})}\cdot \frac {exp(z^{(2)}_{2})}{\sum exp(z^{(2)})}
=(-1)\cdot p(y=1)p(y=2)
$$

$$
\Rightarrow
\frac {\partial J}{\partial z^{(2)}_{1}}
=(-1)\cdot \frac {1(y=1)}{p(y=1)}\cdot (p(y=1)-(p(y=1))^2)
+(-1)\cdot \frac {1(y=2)}{p(y=2)}\cdot (-1)\cdot p(y=1)p(y=2) \
=(-1)\cdot 1(y=1)\cdot (1-p(y=1))
+1(y=2)\cdot p(y=1)
=p(y=1)-1(y=1)
$$

$$
\Rightarrow
\frac {\partial J}{\partial z^{(2)}_{2}}
=p(y=2)-1(y=2)
$$

$$
\Rightarrow \frac {\partial J}{\partial z^{(2)}}
=[p(y=1)-1(y=1), p(y=2)-1(y=2)]^{T}
$$

计算输出层权重向量梯度

$$
\frac {\partial J}{\partial W^{(2)}{1,1}}
=\frac {\partial J}{\partial z^{(2)}{1}}\cdot \frac {\partial z^{(2)}{1}}{\partial W^{(2)}{1,1}}
=(p(y=1)-1(y=1))\cdot a^{(1)}_{1}
$$

$$
\frac {\partial J}{\partial W^{(2)}{1,2}}
=\frac {\partial J}{\partial z^{(2)}{1}}\cdot \frac {\partial z^{(2)}{1}}{\partial W^{(2)}{1,2}}
=(p(y=1)-1(y=1))\cdot a^{(1)}_{2}
$$

$$
\frac {\partial J}{\partial W^{(2)}{1,3}}
=\frac {\partial J}{\partial z^{(2)}{1}}\cdot \frac {\partial z^{(2)}{1}}{\partial W^{(2)}{1,3}}
=(p(y=1)-1(y=1))\cdot a^{(1)}_{3}
$$

$$
\frac {\partial J}{\partial W^{(2)}{1,4}}
=\frac {\partial J}{\partial z^{(2)}{1}}\cdot \frac {\partial z^{(2)}{1}}{\partial W^{(2)}{1,4}}
=(p(y=1)-1(y=1))\cdot a^{(1)}_{4}
$$

$$
\frac {\partial J}{\partial W^{(2)}{2,1}}
=\frac {\partial J}{\partial z^{(2)}{2}}\cdot \frac {\partial z^{(2)}{2}}{\partial W^{(2)}{2,1}}
=(p(y=2)-1(y=2))\cdot a^{(1)}_{1}
$$

$$
\frac {\partial J}{\partial W^{(2)}{2,2}}
=\frac {\partial J}{\partial z^{(2)}{2}}\cdot \frac {\partial z^{(2)}{2}}{\partial W^{(2)}{2,2}}
=(p(y=2)-1(y=2))\cdot a^{(1)}_{2}
$$

$$
\frac {\partial J}{\partial W^{(2)}{2,3}}
=\frac {\partial J}{\partial z^{(2)}{2}}\cdot \frac {\partial z^{(2)}{2}}{\partial W^{(2)}{2,3}}
=(p(y=2)-1(y=2))\cdot a^{(1)}_{3}
$$

$$
\frac {\partial J}{\partial W^{(2)}{2,4}}
=\frac {\partial J}{\partial z^{(2)}{2}}\cdot \frac {\partial z^{(2)}{2}}{\partial W^{(2)}{2,4}}
=(p(y=2)-1(y=2))\cdot a^{(1)}_{4}
$$

$$
\Rightarrow
\frac {\partial J}{\partial W^{(2)}}
=\begin{bmatrix}
\frac {\partial J}{\partial W^{(2)}{1,1}} & \frac {\partial J}{\partial W^{(2)}{1,2}} & \frac {\partial J}{\partial W^{(2)}{1,3}} & \frac {\partial J}{\partial W^{(2)}{1,4}}\
\frac {\partial J}{\partial W^{(2)}{2,1}} & \frac {\partial J}{\partial W^{(2)}{2,2}} & \frac {\partial J}{\partial W^{(2)}{2,3}} & \frac {\partial J}{\partial W^{(2)}{2,4}}
\end{bmatrix}
$$

$$
=\begin{bmatrix}
(p(y=1)-1(y=1))\cdot a^{(1)}{1} & (p(y=1)-1(y=1))\cdot a^{(1)}{2} & (p(y=1)-1(y=1))\cdot a^{(1)}{3} & (p(y=1)-1(y=1))\cdot a^{(1)}{4}\
(p(y=2)-1(y=2))\cdot a^{(1)}{1} & (p(y=2)-1(y=2))\cdot a^{(1)}{2} & (p(y=2)-1(y=2))\cdot a^{(1)}{3} & (p(y=2)-1(y=2))\cdot a^{(1)}{4}
\end{bmatrix}
$$

$$
=\begin{bmatrix}
p(y=1)-1(y=1)\
p(y=2)-1(y=2)
\end{bmatrix}
\begin{bmatrix}
a^{(1)}{1}\
a^{(1)}{2}\
a^{(1)}{3}\
a^{(1)}{4}
\end{bmatrix}
=R^{2\times 1}\cdot R^{1\times 4}
=R^{2\times 4}
$$

计算隐藏层输出向量梯度

$$
\frac {\partial J}{\partial a^{(1)}{1}}
=\frac {\partial J}{\partial z^{(2)}{1}}\cdot \frac {\partial z^{(2)}{1}}{\partial a^{(1)}{1}}
+\frac {\partial J}{\partial z^{(2)}{2}}\cdot \frac {\partial z^{(2)}{2}}{\partial a^{(1)}{1}}
=(p(y=1)-1(y=1))\cdot W^{(2)}{1,1}
+(p(y=2)-1(y=2))\cdot W^{(2)}_{2,1}
$$

$$
\frac {\partial J}{\partial a^{(1)}{2}}
=\frac {\partial J}{\partial z^{(2)}{1}}\cdot \frac {\partial z^{(2)}{1}}{\partial a^{(1)}{2}}
+\frac {\partial J}{\partial z^{(2)}{2}}\cdot \frac {\partial z^{(2)}{2}}{\partial a^{(1)}{2}}
=(p(y=1)-1(y=1))\cdot W^{(2)}{1,2}
+(p(y=2)-1(y=2))\cdot W^{(2)}_{2,2}
$$

$$
\frac {\partial J}{\partial a^{(1)}{3}}
=\frac {\partial J}{\partial z^{(2)}{1}}\cdot \frac {\partial z^{(2)}{1}}{\partial a^{(1)}{3}}
+\frac {\partial J}{\partial z^{(2)}{2}}\cdot \frac {\partial z^{(2)}{2}}{\partial a^{(1)}{3}}
=(p(y=1)-1(y=1))\cdot W^{(2)}{1,3}
+(p(y=2)-1(y=2))\cdot W^{(2)}_{2,3}
$$

$$
\frac {\partial J}{\partial a^{(1)}{4}}
=\frac {\partial J}{\partial z^{(2)}{1}}\cdot \frac {\partial z^{(2)}{1}}{\partial a^{(1)}{4}}
+\frac {\partial J}{\partial z^{(2)}{2}}\cdot \frac {\partial z^{(2)}{2}}{\partial a^{(1)}{4}}
=(p(y=1)-1(y=1))\cdot W^{(2)}{1,4}
+(p(y=2)-1(y=2))\cdot W^{(2)}_{2,4}
$$

$$
\Rightarrow \frac {\partial J}{\partial a^{(1)}}
=\begin{bmatrix}
W^{(2)}{1,1} & W^{(2)}{2,1}\
W^{(2)}{1,2} & W^{(2)}{2,2}\
W^{(2)}{1,3} & W^{(2)}{2,3}\
W^{(2)}{1,4} & W^{(2)}{2,4}
\end{bmatrix}
\begin{bmatrix}
p(y=1)-1(y=1)\
p(y=2)-1(y=2)
\end{bmatrix}
=R^{4\times 2}\cdot R^{2\times 1}
=R^{4\times 1}
$$

计算隐藏层输入向量的梯度

$$
\frac {\partial J}{\partial z^{(1)}{1}}
=\frac {\partial J}{\partial a^{(1)}{1}}\cdot \frac {\partial a^{(1)}{1}}{\partial z^{(1)}{1}}
=((p(y=1)-1(y=1))\cdot W^{(2)}{1,1}
+(p(y=2)-1(y=2))\cdot W^{(2)}{2,1})\cdot 1(z^{(1)}_{1}\geq 0)
$$

$$
\frac {\partial J}{\partial z^{(1)}{2}}
=\frac {\partial J}{\partial a^{(1)}{2}}\cdot \frac {\partial a^{(1)}{2}}{\partial z^{(1)}{2}}
=((p(y=1)-1(y=1))\cdot W^{(2)}{1,2}
+(p(y=2)-1(y=2))\cdot W^{(2)}{2,2})\cdot 1(z^{(1)}_{2}\geq 0)
$$

$$
\frac {\partial J}{\partial z^{(1)}{3}}
=\frac {\partial J}{\partial a^{(1)}{3}}\cdot \frac {\partial a^{(1)}{3}}{\partial z^{(1)}{3}}
=((p(y=1)-1(y=1))\cdot W^{(2)}{1,3}
+(p(y=2)-1(y=2))\cdot W^{(2)}{2,3})\cdot 1(z^{(1)}_{3}\geq 0)
$$

$$
\frac {\partial J}{\partial z^{(1)}{4}}
=\frac {\partial J}{\partial a^{(1)}{4}}\cdot \frac {\partial a^{(1)}{4}}{\partial z^{(1)}{4}}
=((p(y=1)-1(y=1))\cdot W^{(2)}{1,4}
+(p(y=2)-1(y=2))\cdot W^{(2)}{2,4})\cdot 1(z^{(1)}_{4}\geq 0)
$$

$$
\Rightarrow \frac {\partial J}{\partial z^{(1)}}
=\frac {\partial J}{\partial a^{(1)}}\cdot \frac {\partial a^{(1)}}{\partial z^{(1)}}
=(
\begin{bmatrix}
W^{(2)}{1,1} & W^{(2)}{2,1}\
W^{(2)}{1,2} & W^{(2)}{2,2}\
W^{(2)}{1,3} & W^{(2)}{2,3}\
W^{(2)}{1,4} & W^{(2)}{2,4}
\end{bmatrix}
\begin{bmatrix}
p(y=1)-1(y=1)\
p(y=2)-1(y=2)
\end{bmatrix}
)
\begin{bmatrix}
1(z^{(1)}{1}\geq 0) \
1(z^{(1)}{2}\geq 0) \
1(z^{(1)}{3}\geq 0) \
1(z^{(1)}{4}\geq 0)
\end{bmatrix}
=(R^{4\times 2}\cdot R^{2\times 1}) R^{4\times 1}
=R^{4\times 1}
$$

计算隐藏层权重向量的梯度

$$
\frac {\partial J}{\partial W^{(1)}{1,1}}
=\frac {\partial J}{\partial z^{(1)}{1}}\cdot
\frac {\partial z^{(1)}{1}}{\partial W^{(1)}{1,1}}
=((p(y=1)-1(y=1))\cdot W^{(2)}{1,1}
+(p(y=2)-1(y=2))\cdot W^{(2)}{2,1})\cdot 1(z^{(1)}{1}\geq 0)\cdot a^{(0)}{1}
$$

$$
\Rightarrow \frac {\partial J}{\partial W^{(1)}{i,j}}
=\frac {\partial J}{\partial z^{(1)}{i}}\cdot
\frac {\partial z^{(1)}{i}}{\partial W^{(1)}{i,j}}
=((p(y=1)-1(y=1))\cdot W^{(2)}{1,i}
+(p(y=2)-1(y=2))\cdot W^{(2)}{2,i})\cdot 1(z^{(1)}{i}\geq 0)\cdot a^{(0)}{j}
$$

$$
\Rightarrow \frac {\partial J}{\partial W^{(1)}{i,:}}
=((p(y=1)-1(y=1))\cdot W^{(2)}{1,i}
+(p(y=2)-1(y=2))\cdot W^{(2)}{2,i})\cdot 1(z^{(1)}{i}\geq 0)\cdot a^{(0)}
$$

$$
\Rightarrow \frac {\partial J}{\partial W^{(1)}}
=\frac {\partial J}{\partial z^{(1)}_{1}}\cdot (a^{(0)})^{T}
=R^{4\times 1}\cdot R^{1\times 3}
=R^{4\times 3}
$$

小结

TestNet网络的前向操作如下：

$$
z^{(1)}
=W^{(1)}\cdot a^{(0)}+b^{(1)}
$$

$$
a^{(1)}
=g(z^{(1)})
$$

$$
z^{(2)}
=W^{(2)}\cdot a^{(1)}+b^{(2)}
$$

$$
h(z^{(2)})
=[p(y=1),p(y=2)]^{T}
=[\frac {exp(z^{(2)}{1})}{\sum exp(z^{(2)})}, \frac {exp(z^{(2)}{2})}{\sum exp(z^{(2)})}]^{T}
$$

$$
J(z^{(2)})=(-1)\cdot 1(y=1)\ln p(y=1)+(-1)\cdot 1(y=2)\ln p(y=2)
$$

反向传播如下：

$$
\frac {\partial J}{\partial z^{(2)}}
=[p(y=1)-1(y=1), p(y=2)-1(y=2)]^{T}
$$

$$
\frac {\partial J}{\partial W^{(2)}}
=\frac {\partial J}{\partial z^{(2)}}\cdot a^{(1)}
=\begin{bmatrix}
p(y=1)-1(y=1)\
p(y=2)-1(y=2)
\end{bmatrix}
\begin{bmatrix}
a^{(1)}{1}\
a^{(1)}{2}\
a^{(1)}{3}\
a^{(1)}{4}
\end{bmatrix}
$$

$$
\frac {\partial J}{\partial a^{(1)}}
=(W^{(2)})^{T}\cdot \frac {\partial J}{\partial z^{(2)}}
=\begin{bmatrix}
W^{(2)}{1,1} & W^{(2)}{2,1}\
W^{(2)}{1,2} & W^{(2)}{2,2}\
W^{(2)}{1,3} & W^{(2)}{2,3}\
W^{(2)}{1,4} & W^{(2)}{2,4}
\end{bmatrix}
\begin{bmatrix}
p(y=1)-1(y=1)\
p(y=2)-1(y=2)
\end{bmatrix}
$$

$$
\frac {\partial J}{\partial z^{(1)}}
=\frac {\partial J}{\partial a^{(1)}}*1(z^{(1)}\geq 0)
=(
\begin{bmatrix}
W^{(2)}{1,1} & W^{(2)}{2,1}\
W^{(2)}{1,2} & W^{(2)}{2,2}\
W^{(2)}{1,3} & W^{(2)}{2,3}\
W^{(2)}{1,4} & W^{(2)}{2,4}
\end{bmatrix}
\begin{bmatrix}
p(y=1)-1(y=1)\
p(y=2)-1(y=2)
\end{bmatrix}
)
*\begin{bmatrix}
1(z^{(1)}{1}\geq 0) \
1(z^{(1)}{2}\geq 0) \
1(z^{(1)}{3}\geq 0) \
1(z^{(1)}{4}\geq 0)
\end{bmatrix}
$$

$$
\frac {\partial J}{\partial W^{(1)}}
=\frac {\partial J}{\partial z^{(1)}_{1}}\cdot (a^{(0)})^{T}
$$

参考反向传导算法和神经网络反向传播的数学原理，设每层输入向量为残差$\delta^{(l)}=\frac{\partial J(W, b)}{\partial z^{(l)}}$，用于表示该层对最终输出值的残差造成的影响；而最终输出值的残差$\delta^{(L)}$就是损失函数对输出层输入向量的梯度

前向传播执行步骤

层与层之间的操作就是输出向量和权值矩阵的加权求和以及对输入向量的函数激活
$$
z^{(l)} = W^{(l)}\cdot a^{(l-1)}+b^{(l)} \
a^{(l)} = g(z^{(l)})
$$
输出层输出结果后，进行评分函数的计算，得到最终的计算结果（以softmax分类为例）
$$
h(z^{(2)})
=[p(y=1),…,p(y=n^{(L)})]^{T}
=[\frac {exp(z^{(2)}{1})}{\sum exp(z^{(2)})}, …,\frac {exp(z^{(2)}{n^{(L)}})}{\sum exp(z^{(2)})}]^{T}
$$
损失函数根据计算结果判断最终损失值（以交叉熵损失为例）
$$
J(z^{(L)})=(-1)\cdot 1(y=1)\ln p(y=1)+…+(-1)\cdot 1(y=n^{(L)})\ln p(y=n^{(L)})
$$

反向传播执行步骤

计算损失函数对于输出层输入向量的梯度(最终层残差)
$$
\delta^{(L)}=
\frac{\varphi J}{\varphi z^{(L)}}
=[p(y=1)-1(y=1), …, p(y=n^{(L)})-1(y=n^{(L)})]^{T}
$$
计算中间隐藏层的残差值（$L-1,L-2,…1$）
$$
\delta^{(l)}=
\frac{\varphi J}{\varphi z^{(l)}}
=(\frac{\varphi J}{\varphi z^{(l+1)}}\cdot \frac{\varphi z^{(l+1)}}{\varphi a^{(l)}})
*\frac{\varphi a^{(l)}}{\varphi z^{(l)}}
=((W^{(l+1)})^{T}\cdot \delta^{(l+1)})
*\frac{\varphi a^{(l)}}{\varphi z^{(l)}}
$$
完成所有的可学习参数（权值矩阵和偏置向量）的梯度计算
$$
\nabla_{W^{(l)}} J(W, b)= \delta^{(l)}\cdot a^{(l-1)}\
\nabla_{b^{(l)}} J(W, b)= \delta^{(l)}
$$
更新权值矩阵和偏置向量
$$
W^{(l)}=W^{(l)}-\alpha\left[\nabla W^{(l)}+\lambda W^{(l)}\right] \
b^{(l)}=b^{(l)}-\alpha \nabla b^{(l)}
$$

初始化数据的必要性

梯度与输入数据呈正相关，权值更新公式如下：

$$
W^{(l)}{i,j} = W^{(l)}{i,j} - \alpha \cdot \frac{\varphi J}{\varphi W^{(l)}_{i,j}}
$$

如果输入数据放大1000倍，那么梯度至少放大1000倍，这时需要极小的$\alpha$才能平衡每次更新的大小，所以初始化数据很有必要