用于大尺度图像分类的极深卷积网络

发表于 更新于 分类于
本文字数： 3k 阅读时长 ≈ 5 分钟

文章very deep convolutional networks for large-scale image recognition对卷积网络深度进行了详细研究，证明了增加模型深度能够有效提高网络性能，其实现的VGGNet在2014年ImageNet的定位（localisation）和分类（classification）比赛中获得第一和第二名

VGGNet在AlexNet模型配置和学习的基础上，参考ZFNet使用更小的感受野和更小的步长，参考OverFeat在整个图像和多个尺度上对网络进行密集的训练和测试。最终，VGGNet使用\(3\times 3\)大小卷积核进行模型深度的研究，在学习过程中使用多尺度图像进行训练和测试

主要内容如下：

  1. 卷积网络配置
  2. 训练和测试细节
  3. 分类实验
  4. 小结

卷积网络配置

通用架构

VGGNet有多个版本，每个模型均包含以下内容

  • 输入数据固定为\(224\times 224\)大小的RGB图像
  • 图像预处理仅执行均值零中心
  • 使用\(3\times 3\)大小的卷积核，某些模型会额外配置\(1\times 1\)大小的卷积核，用于跨通道信息交互
  • 步长固定为1，零填充用于保证卷积操作不改变输入数据体空间尺寸，\(3\times 3\)大小卷积核对应的零填充是1
  • 每个模型共有5个最大池化层，用于空间池化，滤波器大小为\(2\times 2\)，步长为2
  • 每个模型都包含3个全连接层，第一二个全连接层的神经元个数是4096，第三个神经元个数是类别数
  • 模型输出结果使用softmax评分函数
  • 所有隐藏层使用ReLU作为激活函数

模型配置

VGGNet共有5个版本，分别命名为A-E

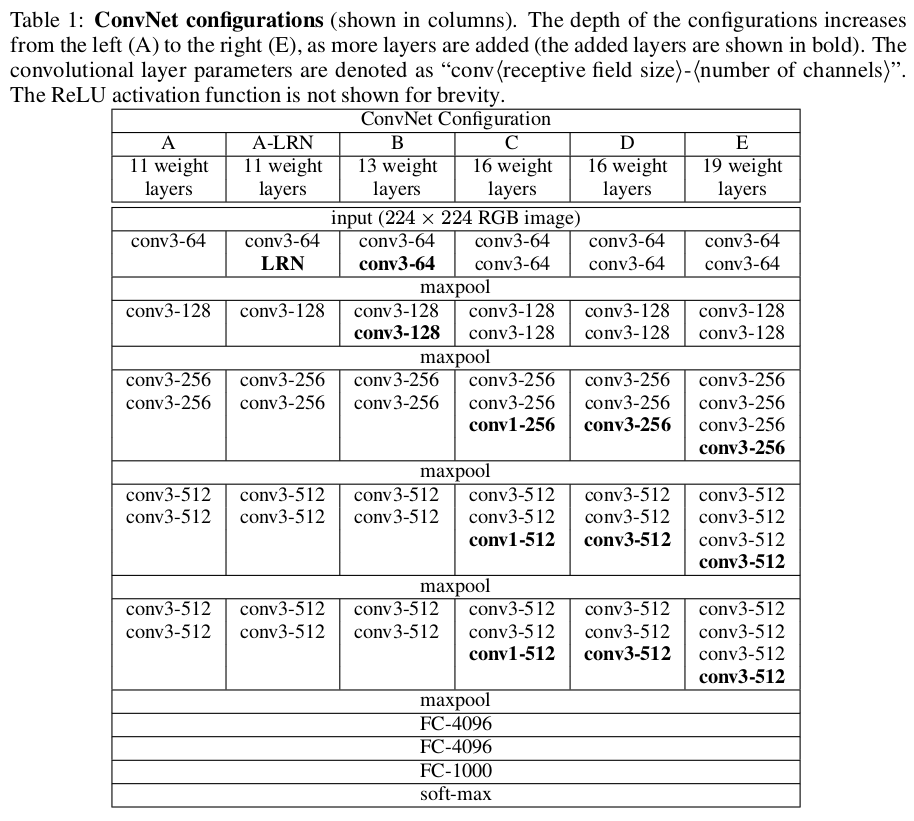
每一列表示一个模型配置，不同列的区别在于增加的卷积层，卷积层命名规则为

conv<卷积核大小>-<滤波器个数>

由于参数主要集中在全连接层，所以5个模型的参数大体一致

小卷积优势

VGGNet使用\(3\times 3\)大小卷积核进行特征提取，多个小卷积核操作的有效感受野等同于大卷积核一次操作。比如，两次\(3\times 3\)大小卷积操作（中间没有池化操作）等同于一次\(5\times 5\)大小卷积操作，三次\(3\times 3\)大小卷积操作的有效感受野等同于一次\(7\times 7\)大小卷积操作，参考感受野尺寸

\(3\times 3\)大小卷积操作还有如下优势：

  1. 每个卷积层包含激活函数运算，堆叠小卷积网络能够集成更多的非线性函数，增强模型判别能力
  2. 假设每个卷积层滤波器个数均为\(C\)通道，那么3次\(3\times 3\)大小卷积操作共有\(3\cdot 3\cdot 3\cdot C = 27C\)个参数，而一次\(7\times 7\)大小卷积操作共有\(49C\)个参数。使用小卷积网络能够降低45%的参数（此处和文章数据不太一致）

在模型C中还使用了\(1\times 1\)大小卷积核，参考NIN，其作用是进行跨通道的信息交互，同时能够集成激活函数，增加判别能力

训练和测试细节

训练

  • 批量大小为\(256\)
  • 动量因子为\(0.9\)
  • 权重惩罚因子为\(5\cdot 10^{-4}\)
  • 第一二个全连接层进行随机失活（失活因子为0.5）
  • 学习率初始化为\(10^{-2}\)，每当验证集精度停止提高时下降10%

整个训练过程共进行370K次（74次迭代），由于更小的卷积核滤波器、更深的深度以及某些层的预初始化，所以网络在较少的迭代次数后就能够拟合

首先对模型A进行训练，参数初始化为零均值，0.01方差；训练完成后使用其参数设置其他模型的1-4层卷积层和最后3个全连接层

训练图像

在每轮迭代中对图像进行随机采样\(224\times 224\)大小，并且进行随机水平翻转以及随机RGB颜色偏移

文章使用多种方法扩充数据集

单尺度图像采样：假设最小边长度为\(S\)，将输入图像最小边缩放到\(S=256或384\)大小，随机采样\(224\times 224\)大小进行训练

多尺度图像采样：将\(S\)随机缩放到尺度[S_{min}, S_{max}]之间（\(S_{min}=256, S_{max}=512\)），再随机采样\(224\times 224\)大小进行训练

测试

将模型全连接层转换成卷积层：第一二个全连接层的卷积核大小为\(7\times 7\)，第三个全连接层的卷积核大小为\(1\times 1\)，最后输出的通道数就是类别成绩

将测试图像最小边缩放至大小\(Q\)，直接应用到全卷积网络，对最后输出的激活图求均值得到类别成绩

同时使用水平翻转扩充测试集，使用最大类后验概率平均原始和翻转图像获得最终的成绩

分类实验

数据集

使用ILSVRC-2012数据集，共1000类，分为3组图像：训练集（130万张）、验证集（5万张）和测试集（10万张）

下面的单尺度、多尺度和多裁剪相对于测试阶段

单尺度评估

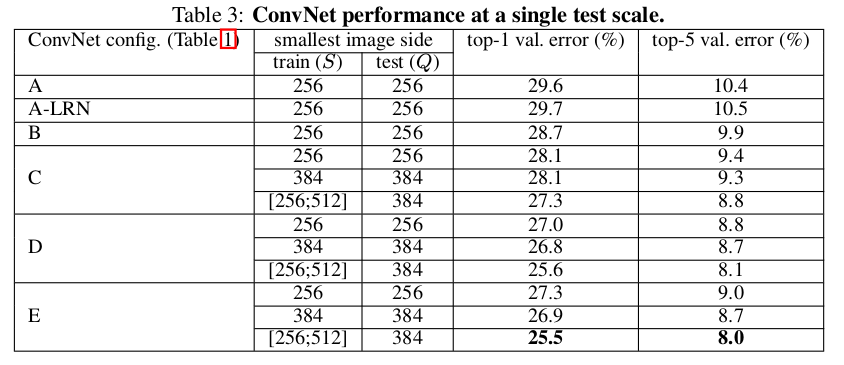
对于固定\(S\)，设置\(Q=S\)，对于\(S\in [S_{min}, S_{max}]\)，设置\(Q=0.5(S_{min}+S_{max})\)

  • 比较模型A和A-LRN，增加LRN层不对实验结果有提高
  • 比较模型A-E，增加模型深度能够提高检测结果
  • 比较模型B、C和D，C比B增加了\(1\times 1\)大小的卷积层，D比B增加了\(3\times 3\)大小的卷积层，实验结果表明虽然增加\(1\times 1\)卷积层能够提高判别能力，但是捕获更多的空间上下文信息更重要
  • 文章用\(5\times 5\)大小卷积核替换模型B的每一对\(3\times 3\)大小卷积核，结果发现更浅的网络比模型B的top-1误差率提高了7%，证明小卷积的深网络比大卷积的浅网络更有效
  • 训练阶段多尺度采样图像比单尺度采样图像的结果更好，表明尺度抖动（scale jittering）能够有效捕获多尺度图像信息

多尺度评估

对于训练集固定\(S\)的情况，测试集采集3张测试图像：\({S-32, S, S+32}\)，平均其检测结果

对于训练集浮动\(S\)的情况，测试集采集更大范围的图像：\({S_{min}, 0.5(S_{min}+S_{max}), S_{max}}\)

测试集尺度抖动能够有效提升检测性能

多裁剪评估

参考：在VGG网络中dense evaluation 与multi-crop evaluation两种预测方法的区别以及效果

比较dense evaluation（密集评估）和multi-crop evaluation（多裁剪评估）

  • 密集评估指直接将原图输入全卷积网络（FCN），最后对每个特征图求均值得到类别成绩

  • 多裁剪评估指对图像进行多次随机裁剪，最后平均每个类别值

通过实验证明两者存在互补性（complementarity），

模型融合

使用模型集成（model ensemble）的方法，组合多个网络进行测试，平均最后的检测结果，能够有效提高检测性能

小结

参考：VGGNet

文章对模型深度进行了详尽的评估，提出的共5个VGGNet模型从11层到19层，证明了堆叠深度能够有效提高网络性能

通过尺度抖动增加训练集，通过多裁剪评估和密集评估融合增加测试集，通过模型集成的方式来提高性能

虽然网络深度的增加能够提高网络性能，但是VGGNet的缺点在于参数多，占用内存大，运算时间长。所以后续的方向一方面在于是否能够减少网络参数，提高运算时间；另一方面在于是否能够堆叠更深的网络来得到更好的性能