卷积神经网络概述

发表于 2019-05-18 更新于 2021-04-27 分类于深度学习/deeplearning 阅读次数：

本文字数： 4.9k 阅读时长 ≈ 9 分钟

卷积神经网络（convolutional neural network）在神经网络（neural network）的基础上进一步发展，实现更强大的分类、识别性能

结合cs231n课程Convolutional Neural Networks: Architectures, Convolution / Pooling Layers，介绍卷积层和池化层，以及基于卷积层、池化层和全连接层的卷积神经网络常用的组成模式

暂不涉及之后发展的网络结构和组成模式

卷积神经网络以神经元为单位进行网络组织，不同于神经网络的2-D处理，卷积神经网络假定输入数据是图像（image），每层的输入输出都是一个3维数据体（3-D volume），各层神经元不仅在2-D空间上进行排列，还在深度（depth）上进行组织

卷积神经网络主要的层类型有卷积层（convolutional layer）、池化层（pooling layer）和全连接层（fully-connected layer）

输入层

输入层不实现任何功能，仅表示输入数据，有3个维度：长度（height）、宽度（width）和深度（depth），其中深度就是图像通道数（channels）

比如cifar-10数据库的图像是$32\times 32$大小的彩色图像，通道数是$3$，所以输入层数据为$32\times 32\times 3$

卷积层

卷积层以滤波器（filter）为单位，滤波器以神经元（neuron）为单位

卷积层有两个特性：局部连接（local connectivity）和参数共享（parameter sharing）

局部连接

滤波器是3维结构，有3个超参数：

长度（height）
宽度（width）
深度（depth）

滤波器神经元和前一层输出数据体局部区域神经元一一连接，其空间尺寸称为感受野（receptive field），也就是滤波器空间大小；滤波器深度和上一层输出数据体的深度一致

比如滤波器大小为$3\times 3\times 6$，那么感受野大小是$3\times 3$，前一层输出数据体的深度是$6$，滤波器神经元个数是$3\cdot 3\cdot 6=54$个

卷积层滤波器空间大小（长度和宽度）通常为$1\times 1$、$3\times 3$或$5\times 5$（奇数结构），滤波器每次只能和前一层输出数据体的局部数据进行交互，然后上下左右移动滤波器，再次进行交互，就像卷积（convolution）操作一样

为保证前一层数据体和滤波器能够完整的执行卷积操作，有以下超参数：

步长（stride）`
零填充（zero-padding）

步长表示滤波器每次移动的步长；零填充用于扩展数据体的边界，控制输出数据体的空间大小

假设输入数据体空间大小为$W$（也就是输入数据体宽度和高度为$W$），感受野大小为$F$，步长大小为$S$，零填充大小为$P$，所以经过滤波器卷积操作后的激活图空间大小为

\[ (W-F+2P)/S+1 \]

比如输入数据体空间大小是$32\times 32$，感受野大小是$5\times 5$，步长为$1$，零填充为$0$，所以激活图大小为

\[ (32-5+2*0)/1+1=28 \]

卷积层包含多个滤波器，每个滤波器和前一层输出数据体进行交互后生成一张2维激活图（activation map），多张激活图在深度方向进行堆叠，输出3维数据体。比如输入数据体大小为$227\times 227\times 3$，卷积层共有$96$个滤波器，滤波器大小为$11\times 11\times 3$，步长为$4$，零填充为$0$，那么输出激活图大小为

\[ (227-11+2*0)/2+1=55 \]

所以输出数据体大小为$55\times 55\times 96$

如果想要输入数据体和输出数据体空间尺寸一致，通常设置$S=1, P=(F-1)/2$，比如$F=3, S=1, P=1$

感受野尺寸

感受野表示卷积层滤波器连接到数据体局部区域的空间尺寸

默认针对上一层输出数据体，称为局部感受野（local receptive field）
针对原始输入图像的局部空间尺寸，称为有效感受野（effective receptive field）

比如原始图像大小为$32\times 32$

如果卷积层滤波器$A$大小为$3\times 3$，步长为$1$，零填充为$0$

第一次卷积操作后激活图空间大小为$30\times 30$；第二次卷积操作后激活图空间大小为$28\times 28$

如果卷积层滤波器$B$大小为$5\times 5$，步长为$1$，零填充为$0$

第一次卷积操作后激活图大小为$28\times 28$

所以滤波器$A$两次卷积操作等同于滤波器$B$一次卷积操作，滤波器$A$第二次卷积操作的局部感受野尺寸为$3\times 3$，有效感受野尺寸为$5\times 5$

类似的，滤波器$A$3次卷积操作等同于$7\times 7$大小的滤波器$C$一次卷积操作，所以$A$第三次卷积操作的有效感受野尺寸为$7\times 7$

参考如何计算感受野(Receptive Field)——原理，使用Receptive Field Calculator能够实现在线计算有效感受野大小

滤波器空间尺寸

通常使用更小的空间尺寸（$3$或者$5$）而不是大的空间尺寸（$7$或者更大）

原因如下：

多次卷积操作能够增加非线性，有利于特征提取
小卷积操作能够减少参数，有利于防止过拟合，增强泛化性。比如每层输出数据通道数均为$C$，那么$(7\times 7\times C)\times C$大小卷积层参数数量为$7\cdot 7\cdot C\cdot C=49C^{2}$，而$(3\times 3\times C)\times C$大小卷积层经过3轮卷积操作后能够实现同样的有效感受野，参数总数是$3\cdot 3\cdot C\cdot C\cdot 3=27C^{2}$

滤波器空间大小为啥是奇数?

偶数空间大小的滤波器同样能够完成卷积操作，不过滤波器空间大小通常选择奇数（3/5/7/9...），参考为什么CNN中的卷积核一般都是奇数奇数，没有偶数偶数的？，有以下原因：

更容易确定中心点
方便对称进行零填充

参数共享

参数共享是卷积操作的特性，也就是滤波器在前一层输出数据体上不同区域进行点积操作时使用同一套参数

cs231n课程的描述意思是因为使用了局部连接和参数共享的特性，所以滤波器操作看起来向卷积操作，所以称为卷积层。不过我感觉是因为要使用卷积操作（因为卷积操作有很好的特征提取能力），所以称为卷积层，有局部连接和参数共享的特征

Notice that if all neurons in a single depth slice are using the same weight vector, then the forward pass of the CONV layer can in each depth slice be computed as a convolution of the neuron’s weights with the input volume (Hence the name: Convolutional Layer). This is why it is common to refer to the sets of weights as a filter (or a kernel), that is convolved with the input.

cs231n课程同样提到另外一种情况：就是对于有明确中心结构的训练图像（比如人脸），期望不同的特征（比如眼睛特征或者头发特征）能够在不同位置被学习，那么可以放松参数共享的限制，称之为局部连接层（Locally-Connected Layer）

卷积层大小评判

假设输入图像尺寸是$32\times 32\times 3$

对于全连接层而言，单个神经元的参数个数是$32\times 32\times 3+1=3073$

如果输入图像尺寸扩展到$227\times 227\times 3$

那么全连接层单个神经元的参数个数是$227\times 227\times 3+1=154588$，

当图像尺寸扩大越50倍后，全连接层单个神经元的参数个数也扩大了约50倍，所以大尺寸图像会导致神经网络计算量爆炸

对于卷积层而言，单个神经元的参数个数是1，假设滤波器大小为$5\times 5\times 3$，共有$16$个滤波器，那么总的参数个数是$5\times 5\times 3\times 16+16=1216$（每个滤波器有一个偏置值），其个数不随图像尺寸而变化

卷积层局部连接和参数共享的特性保证了参数个数不随图像尺寸变化，这允许卷积神经网络在大尺寸图像上进行有效计算，而大尺寸图像也能够提供更多的信息

小结

假设输入数据体为$W_{1}\times H_{1}\times D_{1}$

卷积层有$K$个滤波器，滤波器空间大小$F$，步长$S$以及零填充$P$

那么输入数据体$W_{2}\times H_{2}\times D_{2}$计算如下

\[ W_{2}=(W_{1}-F+2P)/S+1\\ H_{2}=(H_{1}-F+2P)/S+1\\ D_{2}=K \]

每个滤波器的参数有$F\cdot F\cdot D_{1}$，总的参数个数是$(F\cdot F\cdot D_{1})\cdot K$，偏置向量个数是$K$

池化层

池化层执行降采样（downsampling）操作，减小数据体空间尺寸，其目的是

减少计算量以及内存缓存
降低参数个数，防止过拟合
增大有效感受野

有两个超参数：

空间尺寸$F$
步长$S$

比如输入数据体大小为$W_{1}\times H_{1}\times D_{1}$

那么输入数据体$W_{2}\times H_{2}\times D_{2}$计算如下

\[ W_{2}=(W_{1}-F)/S+1\\ H_{2}=(H_{1}-F)/S+1\\ D_{2}=D_{1} \]

最常用的池化层运算是对前一层输出数据体的每一个激活图执行$\max$运算，类似于卷积操作：对每个$2\times 2$大小的数据进行$\max$运算，然后左右移动$S$个距离后再次进行

常用的超参数组合有$F=2, S=2$，以及$F=3, S=2$（这也称为重叠池化层（overlapping pooling））

全连接层

卷积神经网络的全连接层和神经网络一致，参考：神经网络概述

网络架构

常用的网络架构如下：

\[ INPUT \rightarrow [[CONV \rightarrow RELU]*N \rightarrow POOL?]*M \rightarrow [FC \rightarrow RELU]*K \rightarrow FC \]

$INPUT$表示输入层
$CONV$表示卷积层
$RELU$表示激活函数操作
$POOL$表示池化层
$FC$表示全连接层
$*$号表示重复操作
$?$号表示可选操作
$N, M, K$表示数字

通常$N\in [0, 3], M\geq 0, K\in [0,3]$

以LeNet-5为例

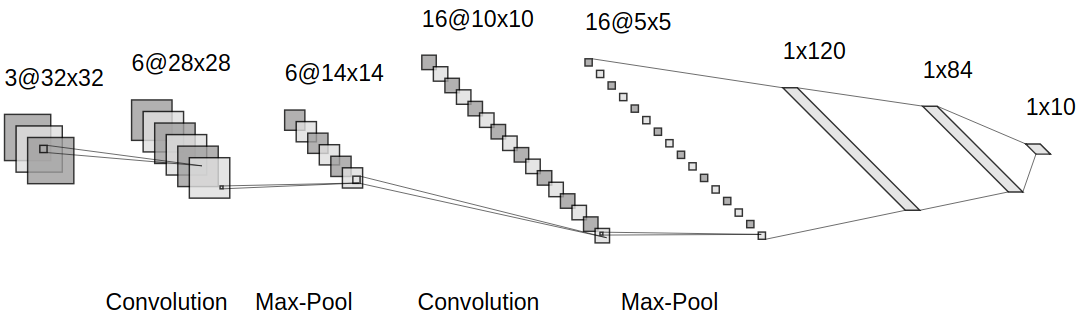
其网络架构为

\[ INPUT \rightarrow [CONV \rightarrow RELU] \rightarrow POOL \rightarrow [CONV \rightarrow RELU] \rightarrow POOL\\ \rightarrow [CONV \rightarrow RELU] \rightarrow [FC \rightarrow RELU] \rightarrow FC \]

所以$N=3, M=2, K=1$

大海