卷积神经网络推导-单张图片矩阵计算
以LeNet-5为例,进行卷积神经网络的矩阵推导
计算符号
参考lecun-98,卷积层标记为\(Cx\),池化层标记为\(Sx\),全连接层标记为\(Fx\),比如\(C1\)表示第一层是卷积层
LeNet-5简介
LeNet-5共有7层(不包含输入层)
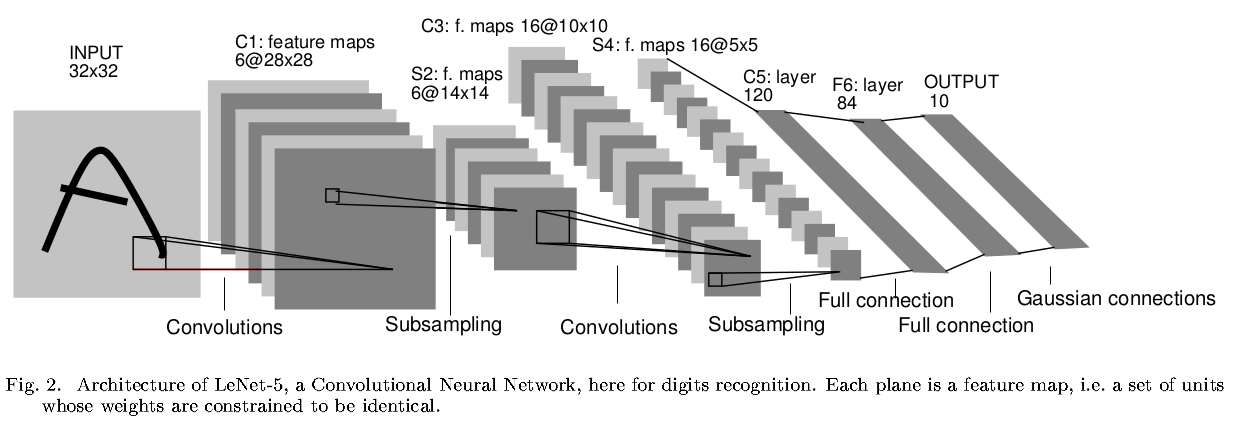
\(C1\)有
6个滤波器,感受野尺寸为\(5\times 5\),步长为\(1\),零填充为\(0\),所以\(C1\)共有\(5\cdot 5\cdot 6+6=156\)个训练参数,输出激活图尺寸为\(28\times 28\)\(S2\)感受野大小为\(2\times 2\),步长为\(2\),将输入数据体4个神经元相加后乘以一个可训练参数,再加上一个偏置值,最后进行\(sigmoid\)操作,所以\(S2\)共有\(2\times 6=12\)个训练参数,输出激活图尺寸为\(14\times 14\)
\(C3\)有
16个滤波器,感受野尺寸为\(5\times 5\),步长为\(1\), 零填充为\(0\),所以输出激活图尺寸为\(10\times 10\)- \(C3\)的滤波器没有和\(S2\)完全连接:前6个滤波器和\(S2\)连续的3个激活图交互,接下来6个滤波器和\(S2\)连续的4个激活图交互,接下来3个滤波器和\(S2\)不连续的4个激活图交互,最后一个滤波器和\(S2\)全连接
- \(C3\)的参数个数是\((5\cdot 5)\cdot (3\cdot 6+4\cdot 6+4\cdot 3+6\cdot 1)+16=1516\)
\(S4\)和\(S2\)一样,所以共有\(2\times 16=32\)个可学习参数,输出激活图尺寸为\(5\times 5\)
\(C5\)有
120个滤波器,感受野大小为\(5\times 5\),步长为\(1\),零填充为\(0\),所以\(C5\)共有\(5\cdot 5\cdot 16\cdot 120+120=48120\)个参数,输出激活图尺寸为\(1\times 1\),输出大小为\(1\times 1\times 120\)\(F6\)有
84个神经元,激活函数是\(tanh\),参数个数是\(120\times 84+84=10164\)个训练参数\(F7\)有
10个神经元,得到84个输入后,不再执行点积运算,而是执行欧氏径向基函数(euclidean radial basis function): \[ y_{i}=\sum_{j}(x_{i}-w_{ij})^{2} \]损失函数是均方误差(
Mean Squared Error, MSE)
最早的LeNet-5在1998年提出,经过多年发展,一些实现细节发生了变化,其中一个版本如下
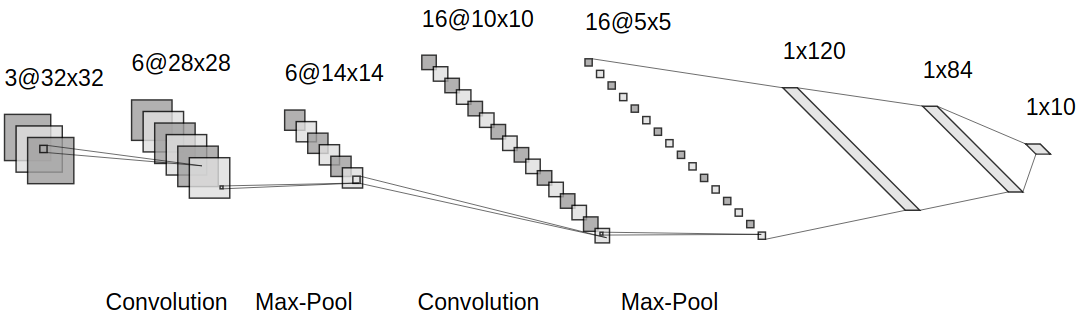
\(C1\)有
6个滤波器,感受野尺寸为\(5\times 5\),步长为\(1\),零填充为\(0\),激活函数是\(relu\),所以\(C1\)共有\(5\cdot 5\cdot 6+6=156\)个训练参数,输出激活图尺寸为\(28\times 28\)\(S2\)感受野大小为\(2\times 2\),步长为\(2\),使用\(\max\)运算,所以输出激活图尺寸为\(14\times 14\)
\(C3\)有
16个滤波器,感受野尺寸为\(5\times 5\),步长为\(1\), 零填充为\(0\),激活函数是\(relu\),所以\(C3\)参数个数是\(5\cdot 5\cdot 6\cdot 16+16=2416\),输出激活图尺寸为\(10\times 10\)\(S4\)和\(S2\)一样,步长为\(2\),使用\(\max\)运算,所以输出激活图尺寸为\(5\times 5\)
\(C5\)有
120个滤波器,感受野大小为\(5\times 5\),步长为\(1\),零填充为\(0\),激活函数为\(relu\),所以\(C5\)共有\(5\cdot 5\cdot 16\cdot 120+120=48120\),输出激活图尺寸为\(1\times 1\),输出大小为\(1\times 120\)\(F6\)有
84个神经元,激活函数是\(relu\),参数个数是\(120\times 84+84=10164\)个训练参数,输出大小为\(1\times 84\)\(F7\)有
10个神经元,参数个数是\(84\times 10+10=850\)个,输出大小为\(1\times 10\)评分函数使用\(softmax\)
损失函数是交叉熵损失(
Cross Entropy Loss)
| 输入 | 卷积核 | 步长 | 零填充 | 输出 | |
|---|---|---|---|---|---|
| C1 | 32x32x3 | 5x5 | 1 | 0 | 28x28x6 |
| S2 | 28x28x6 | 2x2 | 2 | \ | 14x14x6 |
| C3 | 14x14x6 | 5x5 | 1 | 0 | 10x10x16 |
| S4 | 10x10x16 | 2x2 | 2 | \ | 5x5x16 |
| C5 | 5x5x16 | 120 | 0 | 0 | 1x120 |
| F6 | 1x120 | 84 | \ | \ | 1x84 |
| F7 | 1x84 | 10 | \ | \ | 1x10 |
卷积层转全连接层
参考:Implementation as Matrix Multiplication
卷积层滤波器在输入数据体的局部区域执行点积操作,将每次局部连接数据体拉伸为行向量,那么卷积操作就等同于矩阵乘法,变成全连接层运算
比如输入图像大小为\(32\times 32\times 3\),卷积层滤波器大小为\(5\times 5\times 3\),步长为\(1\),零填充为\(0\),共有6个
那么等同于全连接层的输入维度为\(5\cdot 5\cdot 3=125\),共有\(((32-5)/1+1)=784\)个局部连接,所以矩阵运算如下:
\[ X\in R^{784\times 125}\\ W\in R^{125\times 6}\\ b\in R^{1\times 6}\\ Y=X\cdot W+B\in R^{784\times 6} \]
得到输出数据\(Y\)后再拉伸回\(55\times 55\times 6\),就是下一层的输入数据体
池化层转全连接层
池化层滤波器在输入数据体的激活图上执行\(\max\)操作,将每次局部连接区域拉伸为行向量,同样可以将池化层操作转换成全连接层操作
比如输入数据体大小为\(28\times 28\times 6\),池化层滤波器空间尺寸\(2\times 2\),步长为\(2\)
那么每次连接的向量大小是\(2\cdot 2=4\),每个激活图共有\((28/2)^{2}=196\)次局部连接,整个输入数据体共有\(196\cdot 6=1176\)次局部连接,所以运算如下:
\[ X\in R^{1176\times 4}\\ Y = \max(X)\in R^{1176\times 1} \]
得到输出数据\(Y\)后再拉伸回\(14\times 14\times 6\),就是下一层的输入数据体
矩阵计算
进行MNIST数据集的分类
前向传播
输入层
\[ X\in R^{32\times 32\times 1} \]
卷积层\(C1\)
共6个滤波器,每个滤波器空间尺寸为\(5\times 5\),步长为\(1\), 零填充为\(0\)
输出空间尺寸为\((32-5-2\cdot 0)/1+1=28\)
所以单次卷积操作的向量大小为\(5\cdot 5\cdot 1=25\),单个滤波器有\(28\cdot 28=784\)个局部连接
\[ a^{(0)}\in R^{784\times 25}\\ W^{(1)}\in R^{25\times 6}\\ b^{(1)}\in R^{1\times 6}\\ \Rightarrow z^{(1)}=a^{(0)}\cdot W^{(1)}+b^{(1)}\in R^{784\times 6}\\ \Rightarrow y^{(1)}=relu(z^{(1)})\\ \]
输出数据体\(output^{(1)}\in R^{28\times 28\times 6}\)
池化层\(S2\)
执行\(\max\)运算,每个滤波器空间尺寸\(2\times 2\),步长为\(2\)
输出空间尺寸为\((28-2)/2+1=14\)
所以单次\(\max\)操作的向量大小为\(2\cdot 2=4\),单个滤波器有\(14\cdot 14\cdot 6=1176\)个局部连接
\[ a^{(1)}\in R^{1176\times 4}\\ z^{(2)}=\max (a^{(1)})\in R^{1176\times 1} \]
\(argz^{(2)} = argmax(a^{(1)})\in R^{1176}\),每个值表示\(a^{(1)}\)中每行最大值下标
输出数据体\(output^{(2)}\in R^{14\times 14\times 6}\)
卷积层\(C3\)
共16个滤波器,每个滤波器空间尺寸为\(5\times 5\),步长为\(1\), 零填充为\(0\)
输出空间尺寸为\((14-5+2\cdot 0)/1+1=10\)
所以单次卷积操作的向量大小为\(5\cdot 5\cdot 6=150\),单个滤波器有\(10\cdot 10=100\)个局部连接
\[ a^{(2)}\in R^{100\times 150}\\ W^{(3)}\in R^{150\times 16}\\ b^{(3)}\in R^{1\times 16}\\ \Rightarrow z^{(3)}=a^{(2)}\cdot W^{(3)}+b^{(3)}\in R^{100\times 16}\\ \Rightarrow y^{(3)}=relu(z^{(3)})\\ \]
输出数据体\(output^{(3)}\in R^{10\times 10\times 16}\)
池化层\(S4\)
执行\(\max\)运算,每个滤波器空间尺寸\(2\times 2\),步长为\(2\)
输出空间尺寸为\((10-2)/2+1=5\)
所以单次\(\max\)操作的向量大小为\(2\cdot 2=4\),单个滤波器有\(5\cdot 5\cdot 16=400\)个局部连接
\[ a^{(3)}\in R^{400\times 4}\\ z^{(4)}=\max (a^{(3)})\in R^{400\times 1} \]
\(argz^{(4)} = argmax(a^{(3)})\in R^{400}\),每个值表示\(a^{(3)}\)中每行最大值下标
输出数据体\(output^{(4)}\in R^{5\times 5\times 16}\)
卷积层\(C5\)
共120个滤波器,每个滤波器空间尺寸为\(5\times 5\),步长为\(1\), 零填充为\(0\)
输出空间尺寸为\((5-5+2\cdot 0)/1+1=1\)
所以单次卷积操作的向量大小为\(5\cdot 5\cdot 16=400\),单个滤波器有\(1\cdot 1=1\)个局部连接
\[ a^{(4)}\in R^{1\times 400}\\ W^{(5)}\in R^{400\times 120}\\ b^{(5)}\in R^{1\times 120}\\ \Rightarrow z^{(5)}=a^{(4)}\cdot W^{(5)}+b^{(5)}\in R^{1\times 120}\\ \Rightarrow y^{(5)}=relu(z^{(5)})\\ \]
输出数据体\(output^{(5)}\in R^{1\times 120}\)
全连接层\(F6\)
神经元个数为\(84\)
\[ a^{(5)}=y^{(5)}\in R^{1\times 120}\\ W^{(6)}\in R^{120\times 84}\\ b^{(6)}\in R^{1\times 84}\\ \Rightarrow z^{(6)}=a^{(5)}\cdot W^{(6)}+b^{(6)}\in R^{1\times 84}\\ \Rightarrow y^{(6)}=relu(z^{(6)})\\ \]
输出数据体\(output^{(6)}\in R^{1\times 84}\)
输出层\(F7\)
神经元个数为\(10\)
\[ a^{(6)}=y^{(6)}\in R^{1\times 84}\\ W^{(7)}\in R^{84\times 10}\\ b^{(7)}\in R^{1\times 10}\\ \Rightarrow z^{(7)}=a^{(6)}\cdot W^{(7)}+b^{(7)}\in R^{1\times 10}\\ \]
输出数据体\(output^{(7)}\in R^{1\times 10}\)
分类概率
\[ probs=h(z^{(7)})=\frac {exp(z^{(7)})}{exp(z^{(7)})\cdot A\cdot B^{T}} \]
\(A\in R^{10\times 1}, B\in R^{10\times 1}\)都是全\(1\)向量
损失值
\[ dataLoss = -\frac {1}{N} 1^{T}\cdot \ln \frac {exp(z^{(7)}* Y\cdot A)}{exp(z^{(7)})\cdot A} \]
\[ regLoss = 0.5\cdot reg\cdot (||W^{(1)}||^{2} + ||W^{(3)}||^{2} + ||W^{(5)}||^{2} + ||W^{(6)}||^{2} + ||W^{(7)}||^{2}) \]
\[ J(z^{(7)})=dataLoss + regLoss \]
\(Y\in R^{1\times 10}\),仅有正确类别为1, 其余为0
反向传播
输出层\(F7\)
求输入向量\(z^{(7)}\)梯度
\[ d(dataloss)=d(1^{T}\cdot \ln \frac {exp(z^{(7)}* Y\cdot A)}{exp(z^{(7)})\cdot A})=tr((probs^{T} - Y^{T})\cdot dz^{(7)}) \]
\[ \Rightarrow D_{z^{(7)}}f(z^{(7)})=probs^{T} - Y^{T}\\ \Rightarrow \bigtriangledown_{z^{(7)}}f(z^{(7)})=probs - Y \]
其他梯度
\[ z^{(7)}=a^{(6)}\cdot W^{(7)}+b^{(7)} \\ dz^{(7)}=da^{(6)}\cdot W^{(7)} + a^{(6)}\cdot dW^{(7)} + db^{(7)}\\ d(dataloss)=tr(D_{z^{(7)}}f(z^{(7)})\cdot dz^{(7)})\\ =tr(D_{z^{(7)}}f(z^{(7)})\cdot (da^{(6)}\cdot W^{(7)} + a^{(6)}\cdot dW^{(7)} + db^{(7)}))\\ =tr(D_{z^{(7)}}f(z^{(7)})\cdot da^{(6)}\cdot W^{(7)}) +tr(D_{z^{(7)}}f(z^{(7)})\cdot a^{(6)}\cdot dW^{(7)}) +tr(D_{z^{(7)}}f(z^{(7)})\cdot db^{(7)})) \]
求权重矩阵\(W^{(7)}\)梯度
\[ d(dataloss)=tr(D_{z^{(7)}}f(z^{(7)})\cdot a^{(6)}\cdot dW^{(7)}) \]
\[ \Rightarrow D_{W^{(7)}}f(W^{(7)})=D_{z^{(7)}}f(z^{(7)})\cdot a^{(6)}\\ \Rightarrow \bigtriangledown_{W^{(7)}}f(W^{(7)})=(a^{(6)})^{T}\cdot \bigtriangledown_{z^{(7)}}f(z^{(7)}) \]
求偏置向量\(b^{(7)}\)梯度
\[ d(dataloss)=tr(D_{z^{(7)}}f(z^{(7)})\cdot db^{(7)})) \]
\[ \Rightarrow D_{b^{(7)}}f(b^{(7)})=D_{z^{(7)}}f(z^{(7)})\\ \Rightarrow \bigtriangledown_{b^{(7)}}f(b^{(7)})=\bigtriangledown_{z^{(7)}}f(z^{(7)}) \]
求上一层输出向量\(a^{(6)}\)梯度
\[ d(dataloss)=tr(D_{z^{(7)}}f(z^{(7)})\cdot da^{(6)}\cdot W^{(7)}) =tr(W^{(7)}\cdot D_{z^{(7)}}f(z^{(7)})\cdot da^{(6)}) \]
\[ \Rightarrow D_{a^{(6)}}f(a^{(6)})=W^{(7)}\cdot D_{z^{(7)}}f(z^{(7)})\\ \Rightarrow \bigtriangledown_{a^{(6)}}f(a^{(6)})=\bigtriangledown_{z^{(7)}}f(z^{(7)})\cdot (W^{(7)})^{T} \]
全连接层\(F6\)
求输入向量\(z^{(6)}\)梯度
\[ a^{(6)}=y^{(6)}=relu(z^{(6)})\\ da^{(6)}=1(z^{(6)}\geq 0)* dz^{(6)} \]
\[ d(dataloss)=tr(D_{a^{(6)}}f(a^{(6)}) da^{(6)})=tr(D_{a^{(6)}}f(a^{(6)})\cdot (1(z^{(6)}\geq 0)* dz^{(6)}))\\ =tr(D_{a^{(6)}}f(a^{(6)})* 1(z^{(6)}\geq 0)^{T}\cdot dz^{(6)}) \]
\[ \Rightarrow D_{z^{(6)}}f(z^{(6)})=D_{a^{(6)}}f(a^{(6)})* 1(z^{(6)}\geq 0)^{T}\\ \Rightarrow \bigtriangledown_{z^{(6)}}f(z^{(6)})=\bigtriangledown_{a^{(6)}}f(a^{(6)})* 1(z^{(6)}\geq 0) \]
其他梯度
\[ z^{(6)}=a^{(5)}\cdot W^{(6)}+b^{(6)} \\ dz^{(6)}=da^{(5)}\cdot W^{(6)}+a^{(5)}\cdot dW^{(6)}+db^{(6)}\\ d(dataloss)=tr(D_{z^{(6)}}f(z^{(6)})\cdot dz^{(6)})\\ =tr(D_{z^{(6)}}f(z^{(6)})\cdot (da^{(5)}\cdot W^{(6)} + a^{(5)}\cdot dW^{(6)} + db^{(6)}))\\ =tr(D_{z^{(6)}}f(z^{(6)})\cdot da^{(5)}\cdot W^{(6)}) +tr(D_{z^{(6)}}f(z^{(6)})\cdot a^{(5)}\cdot dW^{(6)}) +tr(D_{z^{(6)}}f(z^{(6)})\cdot db^{(6)})) \]
求权重矩阵\(w^{(6)}\)梯度
\[ d(dataloss)=tr(D_{z^{(6)}}f(z^{(6)})\cdot a^{(5)}\cdot dW^{(6)}) \]
\[ \Rightarrow D_{W^{(6)}}f(W^{(6)})=D_{z^{(6)}}f(z^{(6)})\cdot a^{(5)}\\ \Rightarrow \bigtriangledown_{W^{(6)}}f(W^{(6)})=(a^{(5)})^{T}\cdot \bigtriangledown_{z^{(6)}}f(z^{(6)}) \]
求偏置向量\(b^{(6)}\)梯度
\[ d(dataloss)=tr(D_{z^{(6)}}f(z^{(6)})\cdot db^{(6)})) \]
\[ \Rightarrow D_{b^{(6)}}f(b^{(6)})=D_{z^{(6)}}f(z^{(6)})\\ \Rightarrow \bigtriangledown_{b^{(6)}}f(b^{(6)})=\bigtriangledown_{z^{(6)}}f(z^{(6)}) \]
求上一层输出向量\(a^{(5)}\)梯度
\[ d(dataloss)=tr(D_{z^{(6)}}f(z^{(6)})\cdot da^{(5)}\cdot W^{(6)}) =tr(W^{(6)}\cdot D_{z^{(6)}}f(z^{(6)})\cdot da^{(5)}) \]
\[ \Rightarrow D_{a^{(5)}}f(a^{(5)})=W^{(6)}\cdot D_{z^{(6)}}f(z^{(6)})\\ \Rightarrow \bigtriangledown_{a^{(5)}}f(a^{(5)})=\bigtriangledown_{z^{(6)}}f(z^{(6)})\cdot (W^{(6)})^{T} \]
卷积层\(C5\)
求输入向量\(z^{(5)}\)梯度
\[ a^{(5)}=y^{(5)}=relu(z^{(5)})\\ da^{(5)}=1(z^{(5)}\geq 0)* dz^{(5)}\\ \]
\[ d(dataloss)=tr(D_{a^{(5)}}f(a^{(5)}) da^{(5)})=tr(D_{a^{(5)}}f(a^{(5)})\cdot (1(z^{(5)}\geq 0)* dz^{(5)}))\\ =tr(D_{a^{(5)}}f(a^{(5)})* 1(z^{(5)}\geq 0)^{T}\cdot dz^{(5)}) \]
\[ \Rightarrow D_{z^{(5)}}f(z^{(5)})=D_{a^{(5)}}f(a^{(5)})* 1(z^{(5)}\geq 0)^{T}\\ \Rightarrow \bigtriangledown_{z^{(5)}}f(z^{(5)})=\bigtriangledown_{a^{(5)}}f(a^{(5)})* 1(z^{(5)}\geq 0) \]
其他梯度
\[ z^{(5)}=a^{(4)}\cdot W^{(5)}+b^{(5)} \\ dz^{(5)}=da^{(4)}\cdot W^{(5)}+a^{(4)}\cdot dW^{(5)}+db^{(5)}\\ d(dataloss)=tr(D_{z^{(5)}}f(z^{(5)})\cdot dz^{(5)})\\ =tr(D_{z^{(5)}}f(z^{(5)})\cdot (da^{(4)}\cdot W^{(5)} + a^{(4)}\cdot dW^{(5)} + db^{(5)}))\\ =tr(D_{z^{(5)}}f(z^{(5)})\cdot da^{(4)}\cdot W^{(5)}) +tr(D_{z^{(5)}}f(z^{(5)})\cdot a^{(4)}\cdot dW^{(5)}) +tr(D_{z^{(5)}}f(z^{(5)})\cdot db^{(5)})) \]
求权重矩阵\(W^{(5)}\)梯度
\[ d(dataloss)=tr(D_{z^{(5)}}f(z^{(5)})\cdot a^{(4)}\cdot dW^{(5)}) \]
\[ \Rightarrow D_{W^{(5)}}f(W^{(5)})=D_{z^{(5)}}f(z^{(5)})\cdot a^{(4)}\\ \Rightarrow \bigtriangledown_{W^{(5)}}f(W^{(5)})=(a^{(4)})^{T}\cdot \bigtriangledown_{z^{(5)}}f(z^{(5)}) \]
求偏置向量\(b^{(5)}\)梯度
\[ d(dataloss)=tr(D_{z^{(5)}}f(z^{(5)})\cdot db^{(5)}) \]
\[ \Rightarrow D_{b^{(5)}}f(b^{(5)})=D_{z^{(5)}}f(z^{(5)})\\ \Rightarrow \bigtriangledown_{b^{(5)}}f(b^{(5)})=\bigtriangledown_{z^{(5)}}f(z^{(5)}) \]
求上一层输出向量\(a^{(4)}\)梯度
\[ d(dataloss)=tr(D_{z^{(5)}}f(z^{(5)})\cdot da^{(4)}\cdot W^{(5)}) =tr(W^{(5)}\cdot D_{z^{(5)}}f(z^{(5)})\cdot da^{(4)}) \]
\[ \Rightarrow D_{a^{(4)}}f(a^{(4)})=W^{(5)}\cdot D_{z^{(5)}}f(z^{(5)})\\ \Rightarrow \bigtriangledown_{a^{(4)}}f(a^{(4)})=\bigtriangledown_{z^{(5)}}f(z^{(5)})\cdot (W^{(5)})^{T} \]
池化层\(S4\)
将\(a^{(4)}\)梯度重置回\(output^{(4)}\)梯度,再重置为\(y^{(4)}\)梯度
因为卷积层\(C5\)滤波器的空间尺寸和\(output^{(4)}\)的空间尺寸一致,所以不需要将\(a^{(4)}\)先转换成\(output^{(4)}\),再转换成\(y^{(4)}\),可以一步到位
求输入向量\(z^{(4)}\)梯度
\[ z^{(4)}\in R^{400\times 1},\ a^{(4)}\in R^{1\times 400}\\ \Rightarrow a^{(4)} = (z^{(4)})^{T}\\ \Rightarrow da^{(4)} = d(z^{(4)})^{T} \]
\[ d(dataloss)=tr(D_{a^{(4)}}f(a^{(4)}) da^{(4)})=tr(D_{a^{(4)}}f(a^{(4)})\cdot d(z^{(4)})^{T})\\ =tr(D_{a^{(4)}}f(a^{(4)})^{T}\cdot dz^{(4)}) \]
\[ \Rightarrow D_{z^{(4)}}f(z^{(4)})=D_{a^{(4)}}f(a^{(4)})^{T}\\ \Rightarrow \bigtriangledown_{z^{(4)}}f(z^{(4)})=D_{a^{(4)}}f(a^{(4)}) \]
上一层输出向量\(a^{(3)}\)梯度
\[ z^{(4)}=\max (a^{(3)})\\ dz^{(4)}=1(a^{(3)}\ is\ the\ max)* da^{(3)} \]
配合\(argz^{(4)}\),最大值梯度和\(z^{(4)}\)一致,其余梯度为\(0\)
\[ d(dataloss)=tr(D_{z^{(4)}}f(z^{(4)}) dz^{(4)})\\ =tr(D_{z^{(4)}}f(z^{(4)})\cdot 1(a^{(3)}\ is\ the\ max)* da^{(3)}) =tr(D_{z^{(4)}}f(z^{(4)})* 1(a^{(3)}\ is\ the\ max)^{T}\cdot da^{(3)} \]
\[ \Rightarrow D_{a^{(3)}}f(a^{(3)})=D_{z^{(4)}}f(z^{(4)})* 1(a^{(3)}\ is\ the\ max)^{T}\\ \Rightarrow \bigtriangledown_{a^{(3)}}f(a^{(3)})=\bigtriangledown_{z^{(4)}}f(z^{(4)})* 1(a^{(3)}\ is\ the\ max) \]
卷积层\(C3\)
将\(a^{(3)}\)梯度重置回\(output^{(3)}\)梯度,再重置为\(y^{(3)}\)梯度
求输入向量\(z^{(3)}\)梯度
\[ y^{(3)} = relu(z^{(3)})\\ dy^{(3)} = 1(z^{(3)} \geq 0)*dz^{(3)} \]
\[ d(dataloss) =tr(D_{y^{(3)}}f(y^{(3)})\cdot dy^{(3)})\\ =tr(D_{y^{(3)}}f(y^{(3)})\cdot (1(z^{(3)} \geq 0)*dz^{(3)}))\\ =tr(D_{y^{(3)}}f(y^{(3)})* 1(z^{(3)} \geq 0)^{T}\cdot dz^{(3)}) \]
\[ \Rightarrow D_{z^{(3)}}f(z^{(3)})=D_{y^{(3)}}f(y^{(3)})* 1(z^{(3)} \geq 0)^{T}\\ \Rightarrow \bigtriangledown_{z^{(3)}}f(z^{(3)})=\bigtriangledown_{y^{(3)}}f(y^{(3)})* 1(z^{(3)} \geq 0) \]
其他梯度
\[ z^{(3)}=a^{(2)}\cdot W^{(3)}+b^{(3)} \\ dz^{(3)}=da^{(2)}\cdot W^{(3)}+a^{(2)}\cdot dW^{(3)}+db^{(3)}\\ d(dataloss)=tr(D_{z^{(3)}}f(z^{(3)})\cdot dz^{(3)})\\ =tr(D_{z^{(3)}}f(z^{(3)})\cdot (da^{(2)}\cdot W^{(3)} + a^{(2)}\cdot dW^{(3)} + db^{(3)}))\\ =tr(D_{z^{(3)}}f(z^{(3)})\cdot da^{(2)}\cdot W^{(3)}) +tr(D_{z^{(3)}}f(z^{(3)})\cdot a^{(2)}\cdot dW^{(3)}) +tr(D_{z^{(3)}}f(z^{(3)})\cdot db^{(3)})) \]
求权重矩阵\(W^{(3)}\)梯度
\[ d(dataloss)=tr(D_{z^{(3)}}f(z^{(3)})\cdot a^{(2)}\cdot dW^{(3)}) \]
\[ \Rightarrow D_{W^{(3)}}f(W^{(3)})=D_{z^{(3)}}f(z^{(3)})\cdot a^{(2)}\\ \Rightarrow \bigtriangledown_{W^{(3)}}f(W^{(3)})=(a^{(2)})^{T}\cdot \bigtriangledown_{z^{(3)}}f(z^{(3)}) \]
求偏置向量\(b^{(3)}\)梯度
\[ d(dataloss)=\frac {1}{N} \sum_{i=1}^{N} tr(D_{z^{(3)}}f(z^{(3)})\cdot db^{(3)}) \]
\[ \Rightarrow D_{b^{(3)}}f(b^{(3)})=\frac {1}{N} \sum_{i=1}^{N} D_{z^{(3)}}f(z^{(3)})\\ \Rightarrow \bigtriangledown_{b^{(3)}}f(b^{(3)})=\frac {1}{N} \sum_{i=1}^{N} \bigtriangledown_{z^{(3)}}f(z^{(3)}) \]
\(N\)表示\(dz^{(3)}\)的行数
求上一层输出向量\(a^{(2)}\)梯度
\[ d(dataloss)=tr(D_{z^{(3)}}f(z^{(3)})\cdot da^{(2)}\cdot W^{(3)}) =tr(W^{(3)}\cdot D_{z^{(3)}}f(z^{(3)})\cdot da^{(2)}) \]
\[ \Rightarrow D_{a^{(2)}}f(a^{(2)})=W^{(3)}\cdot D_{z^{(3)}}f(z^{(3)})\\ \Rightarrow \bigtriangledown_{a^{(2)}}f(a^{(2)})=\bigtriangledown_{z^{(3)}}f(z^{(3)})\cdot (W^{(3)})^{T} \]
池化层\(S2\)
\(C3\)输入层梯度大小为\(100\times 150\),是在\(S2\)输出数据体\(output^{(2)}\)上采样获得,将\(da^{(2)}\)重采样回\(output^{(2)}\)梯度矩阵,再重置回\(1176\times 1\)大小,就是\(z^{(2)}\)的梯度
上一层输出向量\(a^{(1)}\)梯度
\[ z^{(2)}=\max (a^{(1)})\\ dz^{(2)}=1(a^{(1)}\ is\ the\ max)* da^{(1)} \]
配合\(argz^{(2)}\),最大值梯度和\(z^{(2)}\)一致,其余梯度为\(0\)
\[ d(dataloss)=tr(D_{z^{(2)}}f(z^{(2)}) dz^{(2)})\\ =tr(D_{z^{(2)}}f(z^{(2)})\cdot 1(a^{(1)}\ is\ the\ max)* da^{(1)}) =tr(D_{z^{(2)}}f(z^{(2)})* 1(a^{(1)}\ is\ the\ max)^{T}\cdot da^{(1)} \]
\[ \Rightarrow D_{a^{(1)}}f(a^{(1)})=D_{z^{(2)}}f(z^{(2)})* 1(a^{(1)}\ is\ the\ max)^{T}\\ \Rightarrow \bigtriangledown_{a^{(1)}}f(a^{(1)})=\bigtriangledown_{z^{(2)}}f(z^{(2)})* 1(a^{(1)}\ is\ the\ max) \]
卷积层\(C1\)
将\(a^{(1)}\)梯度重置回\(output^{(1)}\)梯度,再重置为\(y^{(1)}\)梯度
求输入向量\(z^{(1)}\)梯度
\[ y^{(1)} = relu(z^{(1)})\\ dy^{(1)} = 1(z^{(1)} \geq 0)*dz^{(1)} \]
\[ d(dataloss) =tr(D_{y^{(1)}}f(y^{(1)})\cdot dy^{(1)})\\ =tr(D_{y^{(1)}}f(y^{(1)})\cdot (1(z^{(1)} \geq 0)*dz^{(1)}))\\ =tr(D_{y^{(1)}}f(y^{(1)})* 1(z^{(1)} \geq 0)^{T}\cdot dz^{(1)}) \]
\[ \Rightarrow D_{z^{(1)}}f(z^{(1)})=D_{y^{(1)}}f(y^{(1)})* 1(z^{(1)} \geq 0)^{T}\\ \Rightarrow \bigtriangledown_{z^{(1)}}f(z^{(1)})=\bigtriangledown_{y^{(1)}}f(y^{(1)})* 1(z^{(1)} \geq 0) \]
其他梯度
\[ z^{(1)}=a^{(0)}\cdot W^{(1)}+b^{(1)} \\ dz^{(1)}=da^{(0)}\cdot W^{(1)}+a^{(0)}\cdot dW^{(1)}+db^{(1)}\\ d(dataloss)=tr(D_{z^{(1)}}f(z^{(1)})\cdot dz^{(1)})\\ =tr(D_{z^{(1)}}f(z^{(1)})\cdot (da^{(0)}\cdot W^{(1)} + a^{(0)}\cdot dW^{(1)} + db^{(1)}))\\ =tr(D_{z^{(1)}}f(z^{(1)})\cdot da^{(0)}\cdot W^{(1)}) +tr(D_{z^{(1)}}f(z^{(1)})\cdot a^{(0)}\cdot dW^{(1)}) +tr(D_{z^{(1)}}f(z^{(1)})\cdot db^{(1)})) \]
求权重矩阵\(W^{(1)}\)梯度
\[ d(dataloss)=tr(D_{z^{(1)}}f(z^{(1)})\cdot a^{(0)}\cdot dW^{(1)}) \]
\[ \Rightarrow D_{W^{(1)}}f(W^{(1)})=D_{z^{(1)}}f(z^{(1)})\cdot a^{(0)}\\ \Rightarrow \bigtriangledown_{W^{(1)}}f(W^{(1)})=(a^{(0)})^{T}\cdot \bigtriangledown_{z^{(1)}}f(z^{(1)}) \]
求偏置向量\(b^{(1)}\)梯度
\[ d(dataloss)=\frac {1}{N} \sum_{i=1}^{N} tr(D_{z^{(1)}}f(z^{(1)})\cdot db^{(1)}) \]
\[ \Rightarrow D_{b^{(1)}}f(b^{(1)})=\frac {1}{N} \sum_{i=1}^{N} D_{z^{(1)}}f(z^{(1)})\\ \Rightarrow \bigtriangledown_{b^{(1)}}f(b^{(1)})=\frac {1}{N} \sum_{i=1}^{N} \bigtriangledown_{z^{(1)}}f(z^{(1)}) \]
\(N\)表示\(dz^{(1)}\)的行数