神经网络实现-numpy

使用numpy实现神经网络模型

• 使用单层神经网络OneNet实现逻辑或、逻辑与和逻辑非分类
• 使用2层神经网络TwoNet实现逻辑异或分类
• 使用3层神经网络ThreeNet实现iris数据集和mnist数据集分类

使用单层神经网络OneNet实现逻辑或、逻辑与和逻辑非分类

使用单层神经网络OneNet

• 输入层有2个神经元
• 输出层有1个神经元
• 评分函数是sigmoid
• 损失函数是交叉熵损失

OneNet就是逻辑回归模型

• $L=1$
• $a^{(0)}\in R^{m\times 2}$
• $W^{(1)}\in R^{2\times 1}$
• $b^{(1)}\in R^{1\times 2}$
• $y\in R^{m\times 1}$，每行数值表示正确类别（0或者1）

前向传播过程

$$\begin{gathered} z^{(1)}=a^{(0)}\cdot W^{(1)}+b^{(1)} \\ h(z^{(1)})=p(y=1)=sigmoid(z^{(1)})=\frac{1}{1+e^{-z^{(1)}}} \end{gathered}$$

所以分类概率是

$$\begin{gathered} probs=[p(y=0),p(y=1)]=[1-h(z^{(1)}),h(z^{(1)})] \\ =[\frac{e^{-z^{(1)}}}{1+e^{-z^{(1)}}}，\frac{1}{1+e^{-z^{(1)}}}]\in R^{m\times 2} \end{gathered}$$

损失值是

$$J(z^{(1)})=-\frac{1}{m}{1}^T\cdot (y\ast \ln h(z^{(1)})+(1-y)\ast \ln (1-h(z^{(1)})))$$

因为OneNet很特殊（类别不是0就是1），所以损失值可以用下式计算

$$J(z^{(1)})=-\frac{1}{m}(y\cdot \ln h(z^{(1)})+(1-y)\cdot \ln (1-h(z^{(1)})))$$

反向传播过程

计算最终残差${\delta }^{(L)}$

$$\begin{gathered} dJ=d(-\frac{1}{m}{1}^T\cdot (y\ast \ln h(z^{(1)})+(1-y)\ast \ln (1-h(z^{(1)})))) \\ =d(-\frac{1}{m}{1}^T\cdot (y\ast \ln h(z^{(1)})))+d(-\frac{1}{m}{1}^T\cdot (1-y)\ast \ln (1-h(z^{(1)}))) \end{gathered}$$

因为

$$\begin{gathered} d(-\frac{1}{m}{1}^T\cdot (y\ast \ln h(z^{(1)})))=d(-\frac{1}{m}{1}^T\cdot (y\ast (h(z^{(1)}{)}^{-1}\cdot dh(z^{(1)}))) \\ =d(-\frac{1}{m}{1}^T\cdot (y\ast (h(z^{(1)}{)}^{-1}\cdot h(z^{(1)})\cdot (1-h(z^{(1)})\ast d{z}^{(1)})))) \\ =d(-\frac{1}{m}{1}^T\cdot (y\ast ((1-h(z^{(1)})\ast d{z}^{(1)})))) \\ =d(-\frac{1}{m}{y}^T\cdot ((1-h(z^{(1)})\ast d{z}^{(1)}))) \\ =d(-\frac{1}{m}{y}^T\ast (1-h(z^{(1)}{)}^T\cdot d{z}^{(1)})) \end{gathered}$$

$$\begin{gathered} d(-\frac{1}{m}{1}^T\cdot (1-y)\ast \ln (1-h(z^{(1)})))=d(-\frac{1}{m}{1}^T\cdot (1-y)\ast ((1-h(z^{(1)}){)}^{-1}\cdot d(1-h(z^{(1)})))) \\ =d(-\frac{1}{m}{1}^T\cdot (1-y)\ast ((1-h(z^{(1)}){)}^{-1}\cdot (-1)\cdot (1-h(z^{(1)}))\cdot h(z^{(1)})\ast d{z}^{(1)})) \\ =d(-\frac{1}{m}{1}^T\cdot (1-y)\ast ((-1)\cdot h(z^{(1)})\ast d{z}^{(1)})) \\ =d(\frac{1}{m}{1}^T\cdot (1-y)\ast (h(z^{(1)})\ast d{z}^{(1)})) \\ =d(\frac{1}{m}(1-y{)}^T\cdot (h(z^{(1)})\ast d{z}^{(1)})) \\ =d(\frac{1}{m}(1-y{)}^T\ast h(z^{(1)}{)}^T\cdot d{z}^{(1)}) \end{gathered}$$

所以

$$\begin{gathered} dJ=d(-\frac{1}{m}{y}^T\ast (1-h(z^{(1)}{)}^T\cdot d{z}^{(1)}))+d(\frac{1}{m}(1-y{)}^T\ast h(z^{(1)}{)}^T\cdot d{z}^{(1)}) \\ =d(\frac{1}{m}((1-y{)}^T\ast h(z^{(1)}{)}^T-y^T\ast (1-h(z^{(1)}{)}^T)\cdot d{z}^{(1)})) \\ =d(\frac{1}{m}(h(z^{(1)}{)}^T-y^T\ast h(z^{(1)}{)}^T-y^T+y^T\ast h(z^{(1)}{)}^T)\cdot d{z}^{(1)})) \\ =d(\frac{1}{m}(h(z^{(1)}{)}^T-y^T)\cdot d{z}^{(1)})) \end{gathered}$$

$$\begin{gathered} D_{z^{(1)}}f(z^{(1)})=\frac{1}{m}\cdot (h(z^{(1)}{)}^T-y^T) \\ {▽}_{z^{(1)}}f(z^{(1)})=\frac{1}{m}\cdot (h(z^{(1)})-y) \end{gathered}$$

因为OneNet是单层神经网络，所以仅有一个权重矩阵和偏置值

$$\begin{gathered} z^{(1)}=a^{(0)}\cdot W^{(1)}+b^{(1)} \\ d{z}^{(1)}=a^{(0)}\cdot d{W}^{(1)}+d{b}^{(1)} \\ dJ=d(\frac{1}{m}(h(z^{(1)}{)}^T-y^T)\cdot d{z}^{(1)})) \\ =d(\frac{1}{m}(h(z^{(1)}{)}^T-y^T)\cdot (a^{(0)}\cdot d{W}^{(1)}+d{b}^{(1)}))) \\ =d(\frac{1}{m}(h(z^{(1)}{)}^T-y^T)\cdot a^{(0)}\cdot d{W}^{(1)})+d(\frac{1}{m}(h(z^{(1)}{)}^T-y^T)\cdot d{b}^{(1)}) \end{gathered}$$

$$\begin{gathered} D_{W^{(1)}}f(W^{(1)})=\frac{1}{m}\cdot (h(z^{(1)}{)}^T-y^T)\cdot a^{(0)} \\ {▽}_{W^{(1)}}f(W^{(1)})=\frac{1}{m}\cdot (a^{(0)}{)}^T\cdot (h(z^{(1)})-y) \end{gathered}$$

$$\begin{gathered} D_{b^{(1)}}f(b^{(1)})=\frac{1}{m}\cdot \sum _{i=1}^m(h(z_i^{(1)}{)}^T-y_i^T) \\ {▽}_{b^{(1)}}f(b^{(1)})=\frac{1}{m}\cdot \sum _{i=1}^m(h(z_i^{(1)})-y_i) \end{gathered}$$

偏置向量需要考虑维数

进行权重更新时添加正则化项

$$W^{(1)}=W^{(1)}-\alpha \cdot ({\mathrm{\nabla }}_{W^{(1)}}J(W,b)+\lambda \sum W^{(1)})$$

numpy实现

# -*- coding: utf-8 -*-

# @Time    : 19-5-17 下午2:54
# @Author  : zj

import matplotlib.pyplot as plt
import numpy as np

# 批量大小
N = 4
# 输入维数
D = 2
# 输出类别
K = 1


def init_weights(inputs, outputs):
    return 0.01 * np.random.normal(loc=0.0, scale=1.0, size=(inputs, outputs))


class OneNet(object):

    def __init__(self, w, b):
        self.w = w
        self.b = b

    def forward(self, inputs):
        """
        前向计算，计算评分函数值
        """
        self.m = inputs.shape[0]
        self.a0 = inputs

        self.z1 = inputs.dot(self.w) + self.b
        self.h = self.sigmoid(self.z1)
        return self.h

    def backward(self, output):
        """
        反向传播，计算梯度
        """
        delta = (self.h - output) / self.m
        self.dw = self.a0.T.dot(delta)
        self.db = np.sum(delta, axis=0)

    def update(self, alpha=1e-3, la=1e-3):
        """
        更新梯度
        """
        self.w = self.w - alpha * (self.dw + la * np.sum(self.w))
        self.b = self.b - alpha * self.db

    def sigmoid(self, inputs):
        return 1.0 / (1 + np.exp(-1 * inputs))

    def get_parameters(self):
        return self.w, self.b


def compute_loss(score, y, beta=0.0001):
    loss = -1.0 / score.shape[0] * (y.T.dot(np.log(score + beta)) + (1 - y).T.dot(np.log(1 - score + beta)))
    return loss[0][0]


def draw(loss_list, title='损失图'):
    plt.title(title)
    plt.ylabel('损失值')
    plt.xlabel('迭代/500次')
    plt.plot(loss_list)
    plt.show()


if __name__ == '__main__':
    w = init_weights(D, K)
    b = init_weights(K, D)
    net = OneNet(w, b)

    input_array = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
    or_array = np.array([[0, 0, 0, 1]]).T
    loss_list = []
    total_loss = 0
    for i in range(200000):
        score = net.forward(input_array)
        total_loss += compute_loss(score, or_array)
        net.backward(or_array)
        net.update()
        if (i % 500) == 499:
            print('epoch: %d loss: %.4f' % (i + 1, total_loss / 500))
            loss_list.append(total_loss / 500)
            total_loss = 0
    w, b = net.get_parameters()
    print('weight: {}'.format(w))
    print('bias: {}'.format(b))

    print('输入  输出  预测成绩')
    score = net.forward(input_array)
    for item in zip(input_array, or_array, score):
        print(item[0], item[1][0], item[2][0])
    draw(loss_list, '逻辑与')

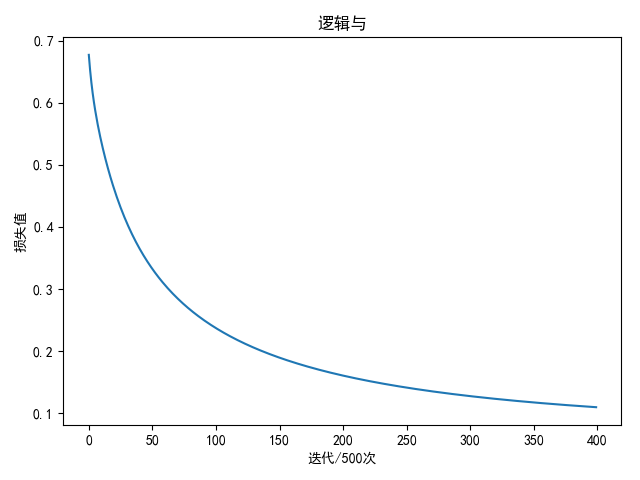
逻辑与

输入值与输出值

• (0,0) - 0
• (0,1) - 0
• (1,0) - 0
• (1,1) - 1

input_array = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
or_array = np.array([[0, 0, 0, 1]]).T

参数如下：

# 批量大小
N = 4
# 输入维数
D = 2
# 输出类别
K = 1
# 学习率
alpha=1e-3
# 正则化强度
la=1e-3

进行2万轮迭代后

weight: [[3.58627447 3.58664415]
 [3.58627445 3.58664413]]
bias: [[-5.69865399 -5.69921649]]
输入  输出  预测成绩
[0 0] 0 0.003339284003451103
[0 1] 0 0.1078994052700841
[1 0] 0 0.1078994065762308
[1 1] 1 0.8136486739472225

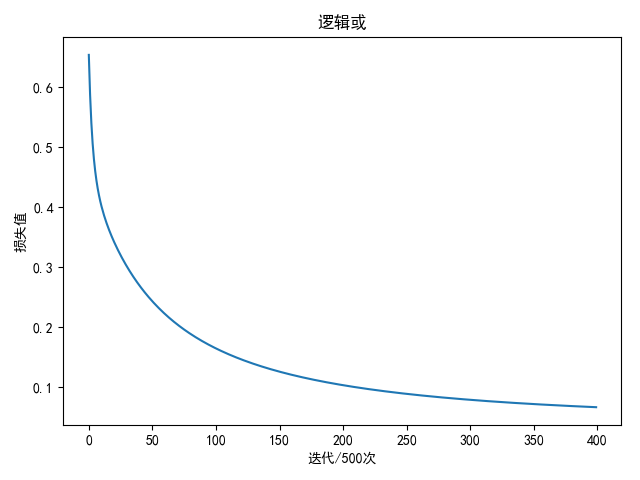
逻辑或

输入值与输出值

• (0,0) - 0
• (0,1) - 1
• (1,0) - 1
• (1,1) - 1

input_array = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
or_array = np.array([[0, 1, 1, 1]]).T

参数如下：

# 批量大小
N = 4
# 输入维数
D = 2
# 输出类别
K = 1
# 学习率
alpha=1e-3
# 正则化强度
la=1e-3

进行2万轮迭代后

weight: [[4.63629047]
 [4.63636187]]
bias: [[-1.87568775]]
输入  输出  预测成绩
[0 0] 0 0.1328849727549866
[0 1] 1 0.9405133604748699
[1 0] 1 0.9405093656227651
[1 1] 1 0.9993872646847757

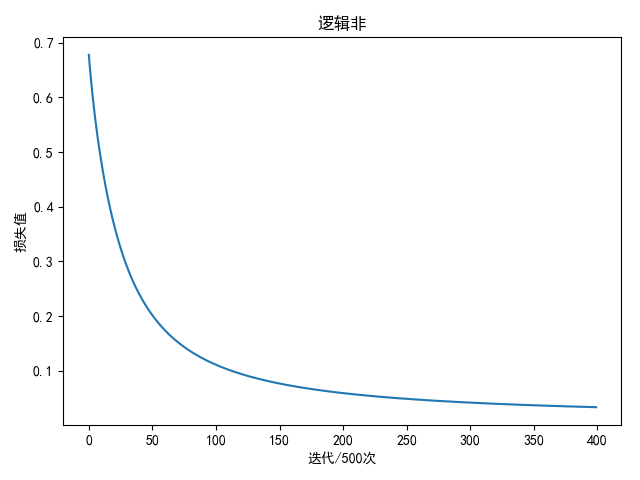
逻辑非

输入值与输出值

• 1. • 0
• 0. • 1

input_array = np.array([[1], [0]])
or_array = np.array([[0, 1]]).T

参数如下：

# 批量大小
N = 2
# 输入维数
D = 1
# 输出类别
K = 1
# 学习率
alpha=1e-3
# 正则化强度
la=1e-3

进行2万轮迭代后

weight: [[-6.79010254]]
bias: [[3.26280938]]
输入  输出  预测成绩
[1] 0 0.02854555463398659
[0] 1 0.9631306816639573

使用2层神经网络TwoNet实现逻辑异或分类

使用2层神经网络TwoNet

• 网络层数$L=2$
• 批量数据$N$
• 输入层神经元个数$D$
• 隐藏层神经元个数$H$
• 输出层神经元个数$K$
• 激活函数是relu
• 评分函数是softmax评分
• 损失函数是交叉熵损失平凡

• $a^{(0)}\in R^{N\times D}$
• $W^{(1)}\in R^{D\times H}$
• $b^{(1)}\in R^{1\times H}$
• $W^{(2)}\in R^{H\times K}$
• $b^{(2)}\in R^{1\times K}$
• $Y\in R^{N\times K}$，每行仅有正确类别为1，其余为0

前向传播过程

$$\begin{gathered} z^{(1)}=a^{(0)}\cdot W^{(1)}+b^{(1)} \\ {a}^{(1)}=relu(z^{(1)}) \\ {z}^{(2)}=a^{(1)}\cdot W^{(2)}+b^{(2)} \end{gathered}$$

所以分类概率是

$$probs=h(z^{(2)})=\frac{exp(z^{(2)})}{exp(z^{(2)})\cdot A\cdot B^T}$$

其中$A\in R^{K\times 1}，B\in R^{K\times 1}$都是全$1$向量，

损失值是

$$dataLoss=-\frac{1}{N}{1}^T\cdot \ln \frac{exp(z^{(2)}\ast Y\cdot A)}{exp(z^2)\cdot A}$$

$$regLoss=0.5\cdot reg\cdot ||W^{(1)}|{|}^2+0.5\cdot reg\cdot ||W^{(2)}|{|}^2$$

$$J(z^{(2)})=dataLoss+regLoss$$

反向传播过程

输出层输入向量梯度

$$\begin{gathered} d(dataloss)=d(-\frac{1}{N}{1}^T\cdot \ln \frac{exp(z^{(2)}\ast Y\cdot A)}{exp(z^2)\cdot A}) \\ =tr(\frac{1}{N}(prob{s}^T-Y^T)\cdot d{z}^{(2)}) \end{gathered}$$

所以

$$\begin{gathered} D_{z^{(2)}}f(z^{(2)})=\frac{1}{N}(prob{s}^T-Y^T) \\ {▽}_{z^{(2)}}f(z^{(2)})=\frac{1}{N}(probs-Y) \end{gathered}$$

对于输出层权重矩阵、偏置向量以及隐藏层输出向量

$$\begin{gathered} z^{(2)}=a^{(1)}\cdot W^{(2)}+b^{(2)} \\ d{z}^{(2)}=d{a}^{(1)}\cdot W^{(2)}+a^{(1)}\cdot d{W}^{(2)}+d{b}^{(2)} \end{gathered}$$

$$\begin{gathered} d(dataloss)=tr(\frac{1}{N}(prob{s}^T-Y^T)\cdot d{z}^{(2)}) \\ =tr(\frac{1}{N}(prob{s}^T-Y^T)\cdot (d{a}^{(1)}\cdot W^{(2)}+a^{(1)}\cdot d{W}^{(2)}+d{b}^{(2)})) \\ tr(\frac{1}{N}(prob{s}^T-Y^T)\cdot d{a}^{(1)}\cdot W^{(2)})+tr(\frac{1}{N}(prob{s}^T-Y^T)\cdot a^{(1)}\cdot d{W}^{(2)})+tr(\frac{1}{N}(prob{s}^T-Y^T)\cdot d{b}^{(2)})) \end{gathered}$$

输出层权重矩阵

$$d(dataloss)=tr(\frac{1}{N}(prob{s}^T-Y^T)\cdot a^{(1)}\cdot d{W}^{(2)})$$

$$\begin{gathered} D_{W^{(2)}}f(W^{(2)})=\frac{1}{N}(prob{s}^T-Y^T)\cdot a^{(1)} \\ {▽}_{W^{(2)}}f(W^{(2)})=\frac{1}{N}(a^{(1)}{)}^T\cdot (probs-Y) \end{gathered}$$

输出层偏置向量

$$d(dataloss)=tr(\frac{1}{N}(prob{s}^T-Y^T)\cdot d{b}^{(2)}))$$

$$\begin{gathered} D_{b^{(2)}}f(b^{(2)})=\frac{1}{N}\sum _{i=1}^N(prob{s}_i^T-Y_i^T) \\ {▽}_{b^{(2)}}f(b^{(2)})=\frac{1}{N}\sum _{i=1}^N(prob{s}_i-Y_i) \end{gathered}$$

隐藏层输出向量

$$d(dataloss)=tr(\frac{1}{N}(prob{s}^T-Y^T)\cdot d{a}^{(1)}\cdot W^{(2)})=tr(\frac{1}{N}{W}^{(2)}\cdot (prob{s}^T-Y^T)\cdot d{a}^{(1)})$$

$$\begin{gathered} D_{a^{(1)}}f(a^{(1)})=\frac{1}{N}{W}^{(2)}\cdot (prob{s}^T-Y^T) \\ {▽}_{a^{(1)}}f(a^{(1)})=\frac{1}{N}(probs-Y)\cdot (W^{(2)}{)}^T \end{gathered}$$

对于隐藏层输入向量

$$\begin{gathered} a^{(1)}=relu(z^{(1)}) \\ d{a}^{(1)}=1(z^{(1)}\ge 0)\ast d{z}^{(1)} \end{gathered}$$

$$\begin{gathered} d(dataloss)=tr(\frac{1}{N}{W}^{(2)}\cdot (prob{s}^T-Y^T)\cdot d{a}^{(1)}) \\ =tr(\frac{1}{N}(W^{(2)}\cdot (prob{s}^T-Y^T))\cdot 1(z^{(1)}\ge 0)\ast d{z}^{(1)}) \\ =tr(\frac{1}{N}(W^{(2)}\cdot (prob{s}^T-Y^T))\ast 1(z^{(1)}\ge 0{)}^T\cdot d{z}^{(1)}) \end{gathered}$$

$$\begin{gathered} D_{z^{(1)}}f(z^{(1)})=\frac{1}{N}(W^{(2)}\cdot (prob{s}^T-Y^T))\ast 1(z^{(1)}\ge 0{)}^T \\ {▽}_{z^{(1)}}f(z^{(1)})=\frac{1}{N}((probs-Y)\cdot (W^{(2)}{)}^T)\ast 1(z^{(1)}\ge 0) \end{gathered}$$

对于隐藏层权重矩阵和偏置值

$$\begin{gathered} z^{(1)}=a^{(0)}\cdot W^{(1)}+b^{(1)} \\ d{z}^{(1)}=d{a}^{(0)}\cdot W^{(1)}+a^{(0)}\cdot d{W}^{(1)}+d{b}^{(1)} \end{gathered}$$

$$\begin{gathered} d(dataloss)=tr(\frac{1}{N}(W^{(2)}\cdot (prob{s}^T-Y^T))\ast 1(z^{(1)}\ge 0{)}^T\cdot d{z}^{(1)}) \\ =tr(\frac{1}{N}(W^{(2)}\cdot (prob{s}^T-Y^T))\ast 1(z^{(1)}\ge 0{)}^T\cdot (d{a}^{(0)}\cdot W^{(1)}+a^{(0)}\cdot d{W}^{(1)}+d{b}^{(1)})) \\ =tr(\frac{1}{N}(W^{(2)}\cdot (prob{s}^T-Y^T))\ast 1(z^{(1)}\ge 0{)}^T\cdot (d{a}^{(0)}\cdot W^{(1)}) \\ +tr(\frac{1}{N}(W^{(2)}\cdot (prob{s}^T-Y^T))\ast 1(z^{(1)}\ge 0{)}^T\cdot a^{(0)}\cdot d{W}^{(1)})+tr(\frac{1}{N}(W^{(2)}\cdot (prob{s}^T-Y^T))\ast 1(z^{(1)}\ge 0{)}^T\cdot d{b}^{(1)}) \end{gathered}$$

输出层权重矩阵

$$d(dataloss)=tr(\frac{1}{N}(W^{(2)}\cdot (prob{s}^T-Y^T))\ast 1(z^{(1)}\ge 0{)}^T\cdot a^{(0)}\cdot d{W}^{(1)})$$

$$\begin{gathered} D_{W^{(1)}}f(W^{(1)})=\frac{1}{N}(W^{(2)}\cdot (prob{s}^T-Y^T))\ast 1(z^{(1)}\ge 0{)}^T\cdot a^{(0)} \\ {▽}_{W^{(1)}}f(W^{(1)})=\frac{1}{N}(a^{(0)}{)}^T\cdot (W^{(2)}\cdot (prob{s}^T-Y^T))\ast 1(z^{(1)}\ge 0) \end{gathered}$$

输出层偏置向量

$$d(dataloss)=tr(\frac{1}{N}(W^{(2)}\cdot (prob{s}^T-Y^T))\ast 1(z^{(1)}\ge 0{)}^T\cdot d{b}^{(1)})$$

$$\begin{gathered} D_{b^{(1)}}f(b^{(1)})=\frac{1}{N}\sum _{i=1}^N(W^{(2)}\cdot (prob{s}^T-Y^T))\ast 1(z^{(1)}\ge 0{)}^T \\ {▽}_{b^{(1)}}f(b^{(1)})=\frac{1}{N}\sum _{i=1}^N((probs-Y)\cdot (W^{(2)}{)}^T)\ast 1(z^{(1)}\ge 0) \end{gathered}$$

numpy实现

# -*- coding: utf-8 -*-

# @Time    : 19-5-17 下午6:45
# @Author  : zj

import matplotlib.pyplot as plt
import numpy as np

# 批量大小
N = 4
# 输入维数
D = 2
# 隐藏层大小
H = 30
# 输出类别
K = 2

# 学习率
learning_rate = 1e-1
# 正则化强度
lambda_rate = 1e-3


def init_weights(inputs, outputs):
    return 0.01 * np.random.normal(loc=0.0, scale=1.0, size=(inputs, outputs))


class TwoNet(object):

    def __init__(self, w, b, w2, b2):
        self.w = w
        self.b = b
        self.w2 = w2
        self.b2 = b2

    def forward(self, inputs):
        """
        前向计算，计算评分函数值
        """
        self.N = inputs.shape[0]
        self.a0 = inputs

        self.z1 = inputs.dot(self.w) + self.b
        self.a1 = np.maximum(0, self.z1)
        self.z2 = self.a1.dot(self.w2) + self.b2
        expscores = np.exp(self.z2)
        self.h = expscores / np.sum(expscores, axis=1, keepdims=True)
        return self.h

    def backward(self, output):
        """
        反向传播，计算梯度
        """
        delta = self.h
        delta[range(self.N), output] -= 1
        delta /= self.N
        self.dw2 = self.a1.T.dot(delta)
        self.db2 = np.sum(delta, axis=0, keepdims=True)

        da1 = delta.dot(self.w2.T)
        dz1 = da1
        dz1[self.z1 < 0] = 0

        self.dw = self.a0.T.dot(dz1)
        self.db = np.sum(dz1, axis=0, keepdims=True)

    def update(self):
        """
        更新梯度
        """
        self.dw2 += lambda_rate * self.w2
        self.dw += lambda_rate * self.w

        self.w2 = self.w2 - learning_rate * self.dw2
        self.b2 = self.b2 - learning_rate * self.b2

        self.w = self.w - learning_rate * self.dw
        self.b = self.b - learning_rate * self.db


def compute_loss(score, y):
    num = score.shape[0]
    data_loss = -1.0 / num * np.sum(np.log(score[range(num), y]))
    # reg_loss = 0.5 * lambda_rate * (np.sum(w ** 2) + np.sum(w2 ** 2))
    return data_loss


def compute_accuracy(y, score):
    predict = np.argmax(score, axis=1)
    return np.mean(predict == y), predict


def draw(loss_list, title='损失图'):
    plt.title(title)
    plt.ylabel('损失值')
    plt.xlabel('迭代/500次')
    plt.plot(loss_list)
    plt.show()


if __name__ == '__main__':
    w = init_weights(D, H)
    b = init_weights(1, H)
    w2 = init_weights(H, K)
    b2 = init_weights(1, K)
    net = TwoNet(w, b, w2, b2)

    input_array = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
    xor_array = np.array([0, 1, 1, 0])
    loss_list = []
    total_loss = 0
    for i in range(10000):
        score = net.forward(input_array)
        total_loss += compute_loss(score, xor_array)
        net.backward(xor_array)
        net.update()
        if (i % 500) == 499:
            print('epoch: %d loss: %.4f' % (i + 1, total_loss / 500))
            loss_list.append(total_loss / 500)
            total_loss = 0
    draw(loss_list, '逻辑异或')

    w, b = net.get_parameters()
    print('weight: {}'.format(w))
    print('bias: {}'.format(b))

    score = net.forward(input_array)
    res, predict = compute_accuracy(xor_array, score)
    print('labels: ' + str(xor_array))
    print('predict: ' + str(predict))
    print('training accuracy: %.2f %%' % (res * 100))

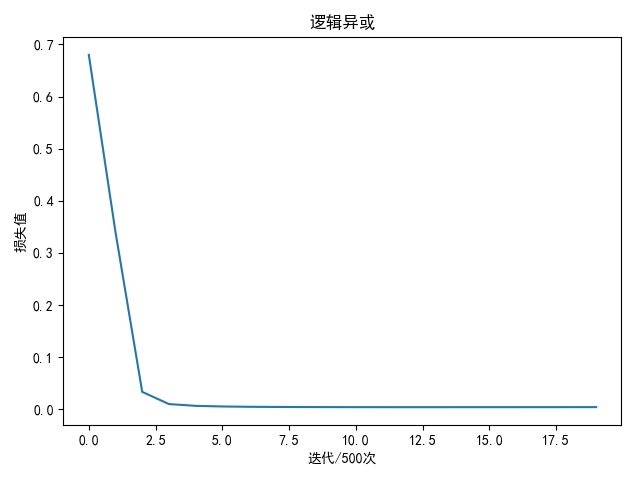
逻辑异或

输入值与输出值

• (0,0) - 0
• (0,1) - 1
• (1,0) - 1
• (1,1) - 0

input_array = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
xor_array = np.array([0, 1, 1, 0])

参数如下：

# 批量大小
N = 4
# 输入维数
D = 2
# 隐藏层大小
H = 6
# 输出类别
K = 2

# 学习率
learning_rate = 1e-1
# 正则化强度
lambda_rate = 1e-3

进行1万轮迭代后

weight: [[-1.39091559  0.26154732 -0.90273461  1.66258303  1.63181952 -1.61815551]
 [ 1.39121663  0.26156278  0.90284832 -1.66206662  1.63189271 -1.61824032]]
bias: [[ 4.92481313e-05 -2.61570825e-01  8.55319233e-06  8.17393648e-05
  -1.63169400e+00  1.61798312e+00]]
labels: [0 1 1 0]
predict: [0 1 1 0]
training accuracy: 100.00 %

使用3层神经网络ThreeNet实现iris数据集和mnist数据集分类

使用3层神经网络ThreeNet

• 网络层数$L=3$
• 批量数据$N$
• 输入层神经元个数$D$
• 第一个隐藏层神经元个数$H1$
• 第二个隐藏层神经元个数$H2$
• 输出层神经元个数$K$
• 激活函数是relu
• 评分函数是softmax评分
• 损失函数是交叉熵损失平凡

• $a^{(0)}\in R^{N\times D}$
• $W^{(1)}\in R^{D\times H1}$
• $b^{(1)}\in R^{1\times H1}$
• $W^{(2)}\in R^{H1\times H2}$
• $b^{(2)}\in R^{1\times H2}$
• $W^{(3)}\in R^{H2\times K}$
• $b^{(3)}\in R^{1\times K}$
• $Y\in R^{N\times K}$，每行仅有正确类别为1，其余为0

前向传播过程

$$\begin{gathered} z^{(1)}=a^{(0)}\cdot W^{(1)}+b^{(1)} \\ {a}^{(1)}=relu(z^{(1)}) \\ {z}^{(2)}=a^{(1)}\cdot W^{(2)}+b^{(2)} \\ {a}^{(2)}=relu(z^{(2)}) \\ {z}^{(3)}=a^{(2)}\cdot W^{(3)}+b^{(3)} \end{gathered}$$

所以分类概率是

$$probs=h(z^{(3)})=\frac{exp(z^{(3)})}{exp(z^{(3)})\cdot A\cdot B^T}$$

其中$A\in R^{K\times 1}，B\in R^{K\times 1}$都是全$1$向量，

损失值是

$$dataLoss=-\frac{1}{N}{1}^T\cdot \ln \frac{exp(z^{(3)}\ast Y\cdot A)}{exp(z^3)\cdot A}$$

$$regLoss=0.5\cdot reg\cdot ||W^{(1)}|{|}^2+0.5\cdot reg\cdot ||W^{(2)}|{|}^2+0.5\cdot reg\cdot ||W^{(3)}|{|}^2$$

$$J(z^{(2)})=dataLoss+regLoss$$

反向传播过程

输出层输入向量梯度

$${▽}_{z^{(3)}}f(z^{(3)})=\frac{1}{N}(probs-Y)$$

对于输出层权重矩阵、偏置向量以及第二个隐藏层输出向量

$${▽}_{W^{(3)}}f(W^{(3)})=\frac{1}{N}(a^{(2)}{)}^T\cdot (probs-Y)$$

$${▽}_{b^{(3)}}f(b^{(3)})=\frac{1}{N}\sum _{i=1}^N(prob{s}_i-Y_i)$$

$${▽}_{a^{(2)}}f(a^{(2)})=\frac{1}{N}(probs-Y)\cdot (W^{(3)}{)}^T$$

对于第二个隐藏层输入向量

$${▽}_{z^{(2)}}f(z^{(2)})=\frac{1}{N}((probs-Y)\cdot (W^{(3)}{)}^T)\ast 1(z^{(2)}\ge 0)$$

对于第二个隐藏层权重矩阵、偏置向量和第一个隐藏层输出向量

$${▽}_{W^{(2)}}f(W^{(2)})=\frac{1}{N}(a^{(1)}{)}^T\cdot ((W^{(3)}\cdot (prob{s}^T-Y^T))\ast 1(z^{(2)}\ge 0))$$

$${▽}_{b^{(2)}}f(b^{(1)})=\frac{1}{N}\sum _{i=1}^N((probs-Y)\cdot (W^{(3)}{)}^T)\ast 1(z^{(2)}\ge 0)$$

$${▽}_{a^{(1)}}f(a^{(1)})=\frac{1}{N}(((probs-Y)\cdot (W^{(3)}{)}^T)\ast 1(z^{(2)}\ge 0))\cdot (W^{(2)}{)}^T$$

对于第一个隐藏层输入向量

$${▽}_{z^{(2)}}f(z^{(2)})=\frac{1}{N}(((probs-Y)\cdot (W^{(3)}{)}^T)\ast 1(z^{(2)}\ge 0)\cdot (W^{(2)}{)}^T)\ast 1(z^{(1)}\ge 0)$$

对于第一个隐藏层权重矩阵和偏置向量

$${▽}_{W^{(2)}}f(W^{(2)})=\frac{1}{N}(a^{(1)}{)}^T\cdot ((((probs-Y)\cdot (W^{(3)}{)}^T)\ast 1(z^{(2)}\ge 0)\cdot (W^{(2)}{)}^T)\ast 1(z^{(1)}\ge 0))$$

$${▽}_{b^{(2)}}f(b^{(1)})=\frac{1}{N}\sum _{i=1}^N(((probs-Y)\cdot (W^{(3)}{)}^T)\ast 1(z^{(2)}\ge 0)\cdot (W^{(2)}{)}^T)\ast 1(z^{(1)}\ge 0)$$

numpy实现

class ThreeNet(object):

    def __init__(self, w, b, w2, b2, w3, b3):
        self.w = w
        self.b = b
        self.w2 = w2
        self.b2 = b2
        self.w3 = w3
        self.b3 = b3

    def forward(self, inputs):
        """
        前向计算，计算评分函数值
        """
        self.N = inputs.shape[0]
        self.a0 = inputs

        self.z1 = inputs.dot(self.w) + self.b
        self.a1 = np.maximum(0, self.z1)

        self.z2 = self.a1.dot(self.w2) + self.b2
        self.a2 = np.maximum(0, self.z2)

        self.z3 = self.a2.dot(self.w3) + self.b3
        expscores = np.exp(self.z3)
        self.h = expscores / np.sum(expscores, axis=1, keepdims=True)
        return self.h

    def backward(self, output):
        """
        反向传播，计算梯度
        """
        delta = self.h
        delta[range(self.N), output] -= 1
        delta /= self.N

        self.dw3 = self.a2.T.dot(delta)
        self.db3 = np.sum(delta, axis=0, keepdims=True)

        da2 = delta.dot(self.w3.T)
        dz2 = da2
        dz2[self.z2 < 0] = 0

        self.dw2 = self.a1.T.dot(dz2)
        self.db2 = np.sum(dz2, axis=0, keepdims=True)

        da1 = dz2.dot(self.w2.T)
        dz1 = da1
        dz1[self.z1 < 0] = 0

        self.dw = self.a0.T.dot(dz1)
        self.db = np.sum(dz1, axis=0, keepdims=True)

    def update(self):
        """
        更新梯度
        """
        self.dw3 += lambda_rate * self.w3
        self.dw2 += lambda_rate * self.w2
        self.dw += lambda_rate * self.w

        self.w3 = self.w3 - learning_rate * self.dw3
        self.b3 = self.b3 - learning_rate * self.b3

        self.w2 = self.w2 - learning_rate * self.dw2
        self.b2 = self.b2 - learning_rate * self.b2

        self.w = self.w - learning_rate * self.dw
        self.b = self.b - learning_rate * self.db

    def __copy__(self):
        w = copy.deepcopy(self.w)
        b = copy.deepcopy(self.b)
        w2 = copy.deepcopy(self.w2)
        b2 = copy.deepcopy(self.b2)
        w3 = copy.deepcopy(self.w3)
        b3 = copy.deepcopy(self.b3)

        net = ThreeNet(w, b, w2, b2, w3, b3)
        return net

iris数据集

分类鸢尾（iris）数据集，下载地址：iris

共4个变量：

• SepalLengthCm - 花萼长度
• SepalWidthCm - 花萼宽度
• PetalLengthCm - 花瓣长度
• PetalWidthCm - 花瓣宽度

以及3个类别：

• Iris-setosa
• Iris-versicolor
• Iris-virginica

网络和训练参数如下：

# 批量大小
N = 120
# 输入维数
D = 4
# 隐藏层大小
H1 = 20
H2 = 20
# 输出类别
K = 3

# 学习率
learning_rate = 5e-2
# 正则化强度
lambda_rate = 1e-3

完整代码如下：

# -*- coding: utf-8 -*-

# @Time    : 19-5-18 下午2:23
# @Author  : zj

# -*- coding: utf-8 -*-

# @Time    : 19-5-18 上午11:48
# @Author  : zj

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import copy
from sklearn import utils
from sklearn.model_selection import train_test_split

# 批量大小
N = 120
# 输入维数
D = 4
# 隐藏层大小
H1 = 20
H2 = 20
# 输出类别
K = 3

# 学习率
learning_rate = 5e-2
# 正则化强度
lambda_rate = 1e-3

data_path = '../data/iris-species/Iris.csv'


def load_data(shuffle=True, tsize=0.8):
    """
    加载iris数据
    """
    data = pd.read_csv(data_path, header=0, delimiter=',')

    if shuffle:
        data = utils.shuffle(data)

    species_dict = {
        'Iris-setosa': 0,
        'Iris-versicolor': 1,
        'Iris-virginica': 2
    }
    data['Species'] = data['Species'].map(species_dict)

    data_x = np.array(
        [data['SepalLengthCm'], data['SepalWidthCm'], data['PetalLengthCm'], data['PetalWidthCm']]).T
    data_y = data['Species']

    x_train, x_test, y_train, y_test = train_test_split(data_x, data_y, train_size=tsize, test_size=(1 - tsize),
                                                        shuffle=False)

    return x_train, x_test, y_train, y_test


def init_weights(inputs, outputs):
    return 0.01 * np.random.normal(loc=0.0, scale=1.0, size=(inputs, outputs))


class ThreeNet(object):
    ...
    ...


def compute_loss(score, y):
    num = score.shape[0]
    data_loss = -1.0 / num * np.sum(np.log(score[range(num), y]))
    # reg_loss = 0.5 * lambda_rate * (np.sum(w ** 2) + np.sum(w2 ** 2))
    return data_loss


def compute_accuracy(score, y):
    predict = np.argmax(score, axis=1)
    return np.mean(predict == y)


def draw(loss_list, title='损失图', ylabel='损失值', xlabel='迭代/100次'):
    plt.title(title)
    plt.ylabel(ylabel)
    plt.xlabel(xlabel)
    plt.plot(loss_list)
    plt.show()


if __name__ == '__main__':
    x_train, x_test, y_train, y_test = load_data(shuffle=True, tsize=0.8)

    w = init_weights(D, H1)
    b = init_weights(1, H1)
    w2 = init_weights(H1, H2)
    b2 = init_weights(1, H2)
    w3 = init_weights(H2, K)
    b3 = init_weights(1, K)
    net = ThreeNet(w, b, w2, b2, w3, b3)

    loss_list = []
    total_loss = 0
    accuracy_list = []
    bestA = 0
    best_net = None
    for i in range(10000):
        score = net.forward(x_train)
        total_loss += compute_loss(score, y_train)
        net.backward(y_train)
        net.update()

        if i % 100 == 99:
            avg_loss = total_loss / 100
            print('epoch: %d loss: %.4f' % (i + 1, avg_loss))
            loss_list.append(avg_loss)
            total_loss = 0

            # 计算训练数据集检测精度
            accuracy = compute_accuracy(net.forward(x_train), y_train)
            accuracy_list.append(accuracy)
            if accuracy >= bestA:
                bestA = accuracy
                best_net = net.__copy__()

    draw(loss_list, 'iris数据集')
    draw(accuracy_list, '训练精度', '检测精度')

    test_score = best_net.forward(x_test)
    res = compute_accuracy(test_score, y_test)
    print('best train accuracy: %.2f %%' % (bestA * 100))
    print('test accuracy: %.2f %%' % (res * 100))

训练1万次结果如下：

best train accuracy: 98.33 %
test accuracy: 100.00 %

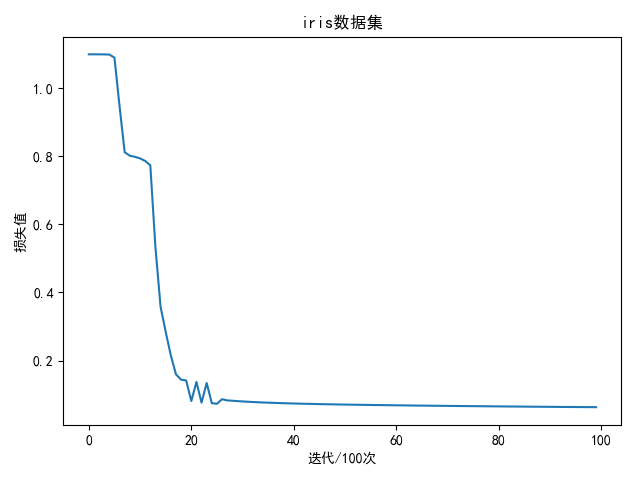
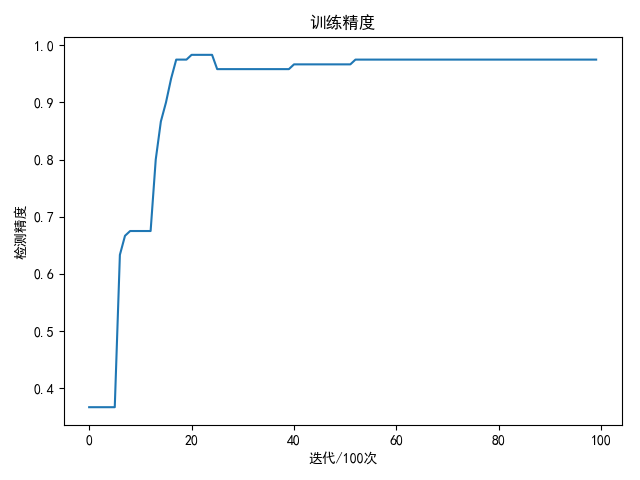
	softmax回归	神经网络
iris	96.67%	98.33%

mnist数据集

mnist数据集是手写数字数据集，共有共有60000张训练图像和10000张测试图像，分别表示数字0-9

数据集的下载和解压参考：Python MNIST解压

网络和训练参数如下：

# 批量大小
batch_size = 256
# 输入维数
D = 784
# 隐藏层大小
H1 = 200
H2 = 80
# 输出类别
K = 10

# 学习率
learning_rate = 1e-3
# 正则化强度
lambda_rate = 1e-3

完整代码如下：

# -*- coding: utf-8 -*-

# @Time    : 19-5-18 上午11:48
# @Author  : zj

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import copy
import cv2
import os
import warnings

warnings.filterwarnings('ignore')

# 批量大小
batch_size = 256
# 输入维数
D = 784
# 隐藏层大小
H1 = 200
H2 = 80
# 输出类别
K = 10

# 学习率
learning_rate = 1e-3
# 正则化强度
lambda_rate = 1e-3

data_path = '../data/mnist/'

cate_list = list(range(10))


def load_data(shuffle=True):
    """
    加载mnist数据
    """
    train_dir = os.path.join(data_path, 'train')
    test_dir = os.path.join(data_path, 'test')

    x_train = []
    x_test = []
    y_train = []
    y_test = []
    train_file_list = []
    for i in cate_list:
        data_dir = os.path.join(train_dir, str(i))
        file_list = os.listdir(data_dir)
        for filename in file_list:
            file_path = os.path.join(data_dir, filename)
            train_file_list.append(file_path)

        data_dir = os.path.join(test_dir, str(i))
        file_list = os.listdir(data_dir)
        for filename in file_list:
            file_path = os.path.join(data_dir, filename)
            img = cv2.imread(file_path, cv2.IMREAD_GRAYSCALE)
            if img is not None:
                h, w = img.shape[:2]
                x_test.append(img.reshape(h * w))
                y_test.append(i)

    train_file_list = np.array(train_file_list)
    if shuffle:
        np.random.shuffle(train_file_list)

    for file_path in train_file_list:
        img = cv2.imread(file_path, cv2.IMREAD_GRAYSCALE)
        if img is not None:
            h, w = img.shape[:2]
            x_train.append(img.reshape(h * w))
            y_train.append(int(os.path.split(file_path)[0].split('/')[-1]))

    return np.array(x_train), np.array(x_test), np.array(y_train), np.array(y_test)


def init_weights(inputs, outputs):
    return 0.01 * np.random.normal(loc=0.0, scale=1.0, size=(inputs, outputs))


class ThreeNet(object):
    ...
    ...


def compute_loss(score, y):
    num = score.shape[0]
    data_loss = -1.0 / num * np.sum(np.log(score[range(num), y]))
    # reg_loss = 0.5 * lambda_rate * (np.sum(w ** 2) + np.sum(w2 ** 2))
    return data_loss


def compute_accuracy(score, y):
    predict = np.argmax(score, axis=1)
    return np.mean(predict == y)


def draw(loss_list, title='损失图', ylabel='损失值', xlabel='迭代/100次'):
    plt.title(title)
    plt.ylabel(ylabel)
    plt.xlabel(xlabel)
    plt.plot(loss_list)
    plt.show()


if __name__ == '__main__':
    x_train, x_test, y_train, y_test = load_data(shuffle=True)

    w = init_weights(D, H1)
    b = init_weights(1, H1)
    w2 = init_weights(H1, H2)
    b2 = init_weights(1, H2)
    w3 = init_weights(H2, K)
    b3 = init_weights(1, K)
    net = ThreeNet(w, b, w2, b2, w3, b3)

    loss_list = []
    total_loss = 0
    accuracy_list = []
    bestA = 0
    best_net = None
    range_list = np.arange(0, x_train.shape[0] - batch_size, step=batch_size)
    for i in range(200):
        for j in range_list:
            data = x_train[j:j + batch_size]
            labels = y_train[j:j + batch_size]

            score = net.forward(data)
            total_loss += compute_loss(score, labels)
            net.backward(labels)
            net.update()

            if j == range_list[-1]:
                avg_loss = total_loss / len(range_list)
                print('epoch: %d loss: %.4f' % (i + 1, avg_loss))
                loss_list.append(avg_loss)
                total_loss = 0

                # 计算训练数据集检测精度
                score = net.forward(x_train[j:j + batch_size])
                accuracy = compute_accuracy(score, labels)
                accuracy_list.append(accuracy)
                if accuracy >= bestA:
                    bestA = accuracy
                    best_net = net.__copy__()
                break

    draw(loss_list, title='mnist', xlabel='迭代/次')
    draw(accuracy_list, title='训练精度', ylabel='检测精度', xlabel='迭代/次')

    test_score = best_net.forward(x_test)
    res = compute_accuracy(test_score, y_test)
    print('best train accuracy: %.2f %%' % (bestA * 100))
    print('test accuracy: %.2f %%' % (res * 100))

训练200次结果如下：

best train accuracy: 100.00 %
test accuracy: 97.92 %

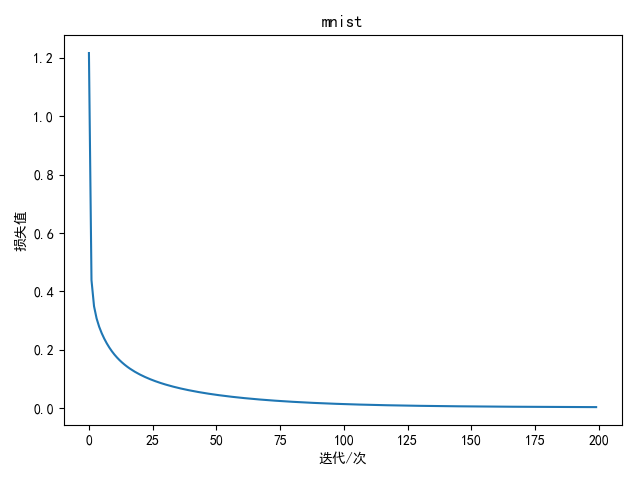
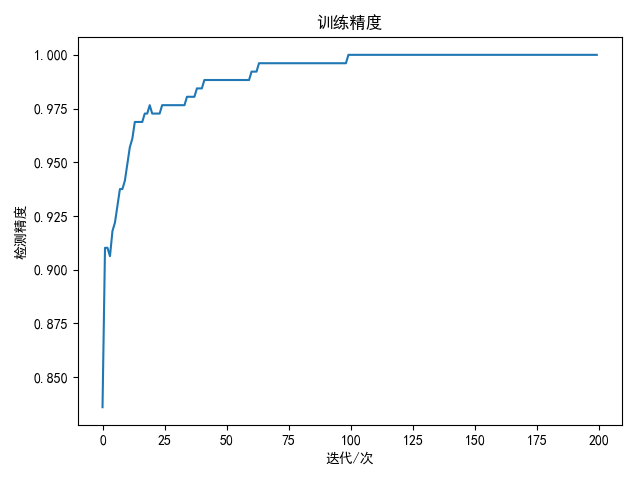
	softmax回归	神经网络
mnist	92.15%	97.92%

相关阅读

• 神经网络概述

• 神经网络推导-批量数据

• 神经网络推导-矩阵计算

• softmax回归

• 使用softmax回归进行mnist分类