高斯滤波

发表于 2019-08-12 更新于 2021-03-30 分类于算法，编程，编程语言，代码库，图像处理，图像滤波阅读次数：

本文字数： 14k 阅读时长 ≈ 25 分钟

在进行图像分割之前通常会使用滤波器进行平滑操作，其目的是消除高斯噪声的影响。学习高斯噪声/高斯滤波的相关概念并实现高斯滤波器

高斯分布

参考：

高斯模糊的原理是什么，怎样在界面中实现？

正态分布

3d绘图

一维高斯分布

$$
G(x) = \frac {1}{\sqrt {2 \pi} \sigma} e^{-\frac {x^{2}}{2\sigma^{2}}}
$$

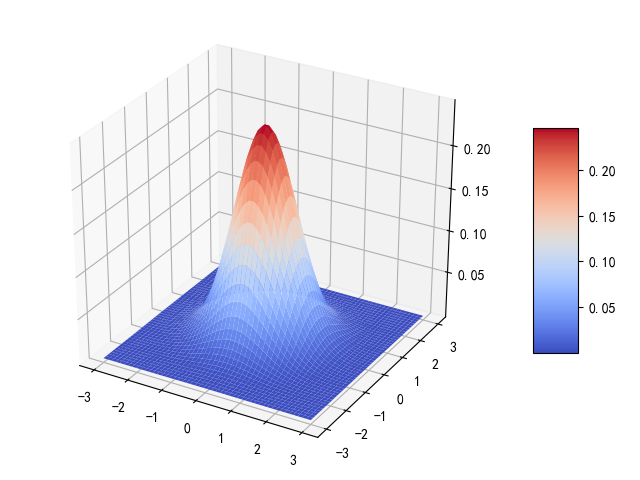
二维高斯分布

$$
G(x, y) = \frac {1}{2 \pi \sigma^{2}} e^{-\frac {x^{2} + y^{2}}{2\sigma^{2}}}
$$

每次计算均以当前像素点为中心，所以均值$\mu$为$0$

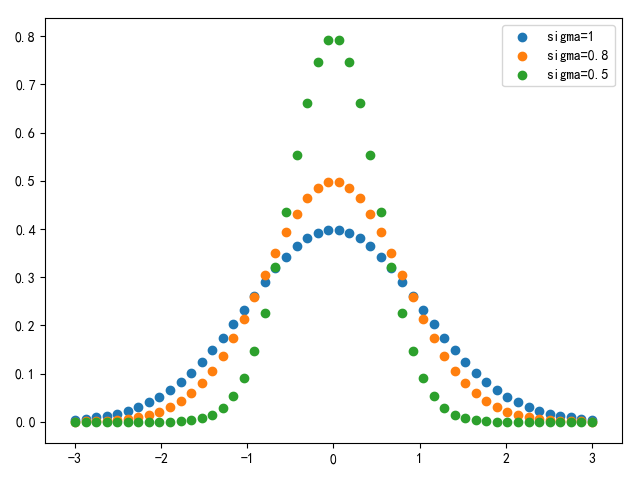
标准差$\sigma$控制离散程度，$\sigma$越大，曲线越扁平，数据分布越离散，滤波效果越明显；$\sigma$越小，曲线越廋高，数据分布越集中，滤波效果不明显

# -*- coding: utf-8 -*-

# @Time    : 19-8-12 下午7:19
# @Author  : zj

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
import math


def gauss_filter_1d(x, sigma=1.):
    w = 1 / (np.sqrt(2 * math.pi) * sigma)
    return np.exp(-1 * x ** 2 / (sigma ** 2 * 2)) * w


def gauss_filter_2d(x, y, sigma=1.):
    w = 1 / (2 * math.pi * sigma ** 2)
    return np.exp(-1 * (x ** 2 + y ** 2) / (sigma ** 2 * 2)) * w


if __name__ == '__main__':
    x = np.linspace(-3, 3, num=50)
    y = np.linspace(-3, 3, num=50)

    X, Y = np.meshgrid(x, y)
    Z = gauss_filter_2d(X, Y, sigma=0.8)

    fig = plt.figure(1)
    ax = fig.add_subplot(111, projection='3d')
    surf = ax.plot_surface(X, Y, Z, cmap=plt.cm.coolwarm)
    fig.colorbar(surf, shrink=0.5, aspect=5)

    fig = plt.figure(2)
    res = gauss_filter_1d(x, sigma=1)
    plt.scatter(x, res, label='sigma=1')
    res = gauss_filter_1d(x, sigma=0.8)
    plt.scatter(x, res, label='sigma=0.8')
    res = gauss_filter_1d(x, sigma=0.5)
    plt.scatter(x, res, label='sigma=0.5')
    plt.legend()

    plt.show()

高斯噪声

参考：高斯噪声

高斯噪声是指它的概率密度函数服从高斯分布（即正态分布）的一类噪声

数字图像中的高斯噪声的主要来源出现在采集期间，由于不良照明/高温引起的传感器噪声

高斯滤波

高斯滤波（gaussian filter）是一种线性平滑滤波，就是对整幅图像进行加权平均的过程，对每个像素点的值，结合邻域内其他像素值进行加权平均

具体操作如下：用一个模板（或称卷积、掩模）扫描图像中的每一个像素，用模板确定的邻域像素的加权平均灰度值去替代模板中心像素点的值

高斯滤波的优点在于消除高斯噪声，其副作用是消除图像细节，所以又称为高斯模糊（gaussian blur）

模板

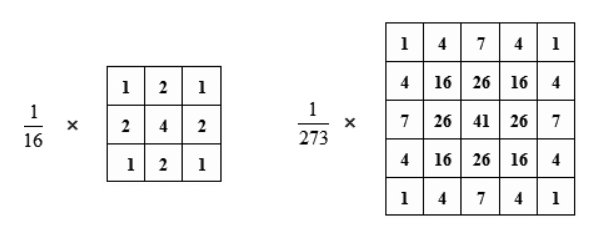
参考：关于高斯滤波的一些理解

有两个常用的高斯模板，分别是$3\times 3$和$5\times 5$大小

滤波过程中的模板是通过高斯公式计算得到的，以$3\times 3$大小模板为例，其原始值是

1
2
3

[[2 1 2]
 [1 0 1]
 [2 1 2]]

假定$\sigma=0.85$，输入到二维高斯函数计算得到

1
2
3

[[0.11759572 0.23493154 0.11759572]
 [0.23493154 0.46934386 0.23493154]
 [0.11759572 0.23493154 0.11759572]]

进行归一化

1
2
3

[[0.06256912 0.12499996 0.06256912]
 [0.12499996 0.24972366 0.12499996]
 [0.06256912 0.12499996 0.06256912]]

除以最小值

1
2
3

[[1 2 1]
 [2 4 2]
 [1 2 1]]

$5\times 5$大小模板同理，不过其$\sigma$约为$1.04$

if __name__ == '__main__':
    x = 5
    y = 5
    sigma = 1.04

    xx = np.abs(np.arange(-1 * (x // 2), x // 2 + 1))
    yy = np.abs(np.arange(-1 * (y // 2), y // 2 + 1))

    xx, yy = np.meshgrid(xx, yy)
    print(xx ** 2 + yy ** 2)
    zz = gauss_filter_2d(xx, yy, sigma=sigma)

    print(zz)
    print(zz / np.sum(zz))
    print((zz / np.min(zz) + 0.5).astype(np.int))

彩色图像

高斯滤波默认对单个通道图像进行，所以对于彩色图像，需要先分离为3个单通道图像，分别进行滤波处理后再合并为3通道图像

opencv实现

参考：

Smoothing.cpp

Gaussian Blurring

opencv提供了高斯滤波以及高斯模板的实现

源码位于：path/to/modules/imgproc/src/smooth.cpp

getGaussianKernel

函数getGaussianKernel()计算并返回高斯滤波系数的$ksize×1$大小矩阵：

$$
G_{i} = \alpha * e^{-(i-(ksize-1)/2)^{2}/(2*sigma^{2})}
$$

参数$ksize$应该是正奇数（1/3/5/...），如果输入为0（即Size(0,0)），则根据sigma值进行计算
参数$\sigma$是高斯标准差，如果输入不为正，根据ksize计算$sigma = 0.3*((ksize-1)\cdot 0.5 - 1)+0.8$，当ksize=3, sigma=0.8，当ksize=5, sigma=1.1
参数$i$遍历$0,…,ksize-1$
参数$\alpha$是缩放因子，其目的是使矩阵归一化：$\sum_{i}G_{i} = 1$

getGaussianKernel源码位于/path/to/modules/imgproc/src/smooth.cpp

当ksize=Size(0,0)时，计算如下：

// automatic detection of kernel size from sigma
if( ksize.width <= 0 && sigma1 > 0 )
    ksize.width = cvRound(sigma1*(depth == CV_8U ? 3 : 4)*2 + 1)|1;
if( ksize.height <= 0 && sigma2 > 0 )
    ksize.height = cvRound(sigma2*(depth == CV_8U ? 3 : 4)*2 + 1)|1;

当sigma=1.0时，ksize.width = cvRound(7)|1 = 0111|1 = 0111 = 7
当sigma=0.8时，ksize.width = cvRound(5.8)|1 = 6|1 = 0110|1 = 0111 = 7
当sigma=0.5时，ksize.width = cvRound(4)|1 = 0100|1 = 0101 = 5

GaussianBlur

函数GaussianBlur()将源图像与高斯核进行卷积操作

使用$(5,5)$大小，$sigma=1$的高斯核进行卷积操作

python语言

import cv2

img = cv2.imread('lena.jpg')
blur = cv2.GaussianBlur(img, (5, 5), 1)
cv2.imshow('img', img)
cv2.imshow('blur', blur)
cv2.waitKey(0)

C++语言

#include <iostream>
#include <opencv2/opencv.hpp>

using namespace std;
using namespace cv;

int main() {
    std::cout << "Hello, World!" << std::endl;

    Mat img = imread("lena.jpg");
    if (img.empty()) {
        std::cout << "error" << std::endl;
        exit(0);
    }

    Mat dst = img.clone();
    GaussianBlur(img, dst, Size(5, 5), 1, 1);

    imshow("img", img);
    imshow("gauss", dst);
    waitKey(0);

    return 0;
}

自定义实现（c++）

创建类GaussianFilter，实现获取高斯滤波功能

使用gaussFilter2d实现高斯分布计算（去掉weight计算，其在归一化过程中不需要）
使用Conv2d实现卷积核与图像计算
使用getGaussianKernel计算高斯模板
使用GaussianBlur进行高斯滤波

//
// Created by zj on 19-8-13.
//

#ifndef OPENCV_PROJECT_GAUSSIANFILTER_H
#define OPENCV_PROJECT_GAUSSIANFILTER_H

#include <cmath>
#include <iostream>
#include <opencv2/opencv.hpp>

using namespace std;
using namespace cv;

class GaussianFilter {

public:
    /**
     * 高斯滤波操作
     */
    void GaussianBlur(Mat &src, Mat &dst, int ksize = 3, double sigma = 1.0);

    /**
     * 生成二维高斯滤波内核
     */
    Mat getGaussianKernel(int ksize, double sigma);

private:
    /**
     * 二维卷积操作
     */
    void Conv2d(Mat &src, Mat &dst, Mat filter);

    /**
     * 二维高斯滤波
     */
    double gaussFilter2d(double x, double y, double sigma = 1.0);
};


#endif //OPENCV_PROJECT_GAUSSIANFILTER_H

//
// Created by zj on 19-8-13.
//

#include "GaussianFilter.h"


void GaussianFilter::GaussianBlur(Mat &src, Mat &dst, int ksize, double sigma) {
    int channels = src.channels();
    Mat filter = getGaussianKernel(ksize, sigma);

    if (channels == 1) {
        Conv2d(src, dst, filter);
    } else {
        vector<Mat> mats;
        vector<Mat> dstMats;
        split(src, mats);
        for (auto srcImg: mats) {
            Mat dstImg = srcImg.clone();

            Conv2d(srcImg, dstImg, filter);
            dstMats.push_back(dstImg);
        }
        merge(dstMats, dst);
    }
}

Mat GaussianFilter::getGaussianKernel(int ksize, double sigma) {
    // ksize=3, sigma=0.85
    // kszie=5, sigma=1.04
    static const double gaussian_kernel_3[][3] = {{0.06256912, 0.12499996, 0.06256912},
                                                  {0.12499996, 0.24972366, 0.12499996},
                                                  {0.06256912, 0.12499996, 0.06256912}};
    static const double gaussian_kernel_5[][5] = {
            {0.00373691, 0.0149557, 0.023745,  0.0149557, 0.00373691},
            {0.0149557,  0.0598552, 0.0950314, 0.0598552, 0.0149557},
            {0.023745,   0.0950314, 0.15088,   0.0950314, 0.023745},
            {0.0149557,  0.0598552, 0.0950314, 0.0598552, 0.0149557},
            {0.00373691, 0.0149557, 0.023745,  0.0149557, 0.00373691},
    };

    Mat res;
    if (ksize == 3) {
        res = Mat(ksize, ksize, CV_64FC1);
        std::memcpy(res.data, gaussian_kernel_3, ksize * ksize * sizeof(double));
    } else if (ksize == 5) {
        res = Mat(ksize, ksize, CV_64FC1);
        std::memcpy(res.data, gaussian_kernel_5, ksize * ksize * sizeof(double));
    } else {
        double kernel[ksize][ksize];
        int radius = ksize / 2;
        double sum = 0;

        for (int i = 0; i < ksize; i++) {
            for (int j = 0; j < ksize; j++) {
                kernel[i][j] = gaussFilter2d(abs(i - radius), abs(j - radius), sigma);
                sum += kernel[i][j];
            }
        }

        for (int i = 0; i < ksize; i++) {
            for (int j = 0; j < ksize; j++) {
                kernel[i][j] = kernel[i][j] / sum;
            }
        }

        res = Mat(ksize, ksize, CV_64FC1);
        std::memcpy(res.data, kernel, ksize * ksize * sizeof(double));
    }

    return res;
}

void GaussianFilter::Conv2d(Mat &src, Mat &dst, Mat filter) {
    int filter_h = filter.rows;
    int filter_w = filter.cols;

    int radius_y = filter_h / 2;
    int radius_x = filter_w / 2;

    int h = src.rows;
    int w = src.cols;

    double temp;
    int target_x;
    int target_y;
    bool flag;
    for (int i = 0; i < h; i++) {
        auto *data = dst.ptr<uchar>(i);
        for (int j = 0; j < w; j++) {
            temp = 0;
            for (int k = 0; k < filter_h; k++) {
                for (int l = 0; l < filter_w; l++) {
                    target_x = j - radius_x + l;
                    target_y = i - radius_y + k;

                    flag = target_x >= 0 and target_x < h and target_y >= 0 and target_y < w;
                    if (flag) {
                        auto *src_data = src.ptr<uchar>(target_y);
                        auto *filter_data = filter.ptr<double>(k);
                        temp += (int) src_data[target_x] * filter_data[l];
                    }
                }
            }
            data[j] = (uchar) round(temp);
        }
    }
}

double GaussianFilter::gaussFilter2d(double x, double y, double sigma) {
//    double weight = 1 / (sqrt(2 * M_PI) * sigma);
//    double temp = -1 * (x * x + y * y) / (2 * sigma * sigma);
//    return weight * exp(temp);
    return exp(-1 * (x * x + y * y) / (2 * sigma * sigma));
}

优化

参考：

算法优化学习：（二）二维高斯滤波的引入

二维高斯模糊和可分离核形式的快速实现

二维高斯分布公式可由两个一维高斯分布公式组成：

$$
G(x,y) = G(x)\cdot G(y)
$$

利用二维高斯模板对图像进行滤波：

$$
f(x,y) = \frac {1}{\sum^{r}{u=-r}\sum^{r}{v=-r}G(u,v)}
\cdot \sum^{r}{u=-r}\sum^{r}{v=-r}G(u,v)\cdot I(x+u,y+v)
$$

其中$I()$表示图像像素值，$r$表示模板半径，模板长宽为$2\cdot r+1$

利用一维高斯分布公式进行优化如下：

$$
f(x,y) = \frac {1}{\sum^{r}{u=-r}\sum^{r}{v=-r}G(u,v)}
\cdot \sum^{r}{u=-r}\sum^{r}{v=-r}G(u,v)\cdot I(x+u,y+v)\
=\frac {1}{\sum^{r}{u=-r}\sum^{r}{v=-r}G(u)\cdot G(v)}
\cdot \sum^{r}{u=-r}\sum^{r}{v=-r}G(u)\cdot G(v)\cdot I(x+u,y+v)\
=\frac {1}{\sum^{r}{u=-r}G(u)\cdot \sum^{r}{v=-r} G(v)}
\cdot \sum^{r}{u=-r}G(u)\cdot \sum^{r}{v=-r} G(v)\cdot I(x+u,y+v)\
=\frac {1}{\sum^{r}{v=-r} G(v)}\cdot \sum^{r}{u=-r}G(u) [
\frac {1}{\sum^{r}{u=-r}G(u)}\cdot \sum^{r}{v=-r} G(v)\cdot I(x+u,y+v)]
$$

可以先在垂直方向对图像进行一维高斯变换，再在水平方向对图像进行一维高斯变换

按照原先的二维模板计算方式，对单个图像像素进行计算需要$(2\cdot r+1)^{2}$次乘法以及$(2\cdot r+1)^{2}-1$次加法，时间复杂度为$O(n^{2})$

如果转换成一维模板计算，先进行垂直方向计算，需要$(2\cdot r+1)$次乘法，$(2\cdot r+1)-1$次加法。对于水平方向计算类似，总共需要$2\cdot(2\cdot r+1)$次乘法，$2\cdot(2\cdot r+1)-2$次加法，时间复杂度为$O(n)$

单单对单个图像像素进行计算不太好理解，好像使用一维模板计算的只是沿该像素点水平和垂直的领域像素，没有涉及到对角领域像素；如果扩大到整副图像就好理解了

修改后的GaussianFilter实现如下：

getGaussianKernel生成一维高斯算子，参考OpenCV实现使用固定模板
GaussianBlur先对水平方向进行高斯滤波，再对垂直方向进行高斯滤波

完整类定义如下：

//
// Created by zj on 19-8-13.
//

#ifndef OPENCV_PROJECT_GAUSSIANFILTER_H
#define OPENCV_PROJECT_GAUSSIANFILTER_H

#include <cmath>
#include <iostream>
#include <opencv2/opencv.hpp>

using namespace std;
using namespace cv;

class GaussianFilter {

public:
    /**
     * 高斯滤波操作
     */
    void GaussianBlur(Mat src, Mat &dst, Size ksize, double sigmaX, double sigmaY = 0);

    /**
     * 生成一维高斯滤波内核
     */
    Mat getGaussianKernel(int ksize, double sigma, int ktype = CV_64F);

private:
    /**
     * 二维卷积操作
     * 边界使用0填充
     */
    void Conv2d(Mat src, Mat &dst, Mat filter);
};


#endif //OPENCV_PROJECT_GAUSSIANFILTER_H

//
// Created by zj on 19-8-13.
//

#include "GaussianFilter.h"

void GaussianFilter::GaussianBlur(Mat src, Mat &dst, Size ksize, double sigmaX, double sigmaY) {
    sigmaY = sigmaY == 0 ? sigmaX : sigmaY;

    int channels = src.channels();
    Mat kernel_x = getGaussianKernel(ksize.width, sigmaX).reshape(1, 1);
    Mat kernel_y = getGaussianKernel(ksize.height, sigmaY);

    Mat tempImg = src.clone();
    if (channels == 1) {
        Conv2d(src, tempImg, kernel_x);
        Conv2d(tempImg, dst, kernel_y);
    } else {
        vector<Mat> mats;
        vector<Mat> dstMats;
        split(src, mats);
        for (auto srcImg: mats) {
            Mat dstImg = srcImg.clone();
            Conv2d(srcImg, tempImg, kernel_x);
            Conv2d(tempImg, dstImg, kernel_y);

            dstMats.push_back(dstImg.clone());
        }
        merge(dstMats, dst);
    }
}

Mat GaussianFilter::getGaussianKernel(int ksize, double sigma, int ktype) {
    const int SMALL_GAUSSIAN_SIZE = 7;
    static const float small_gaussian_tab[][SMALL_GAUSSIAN_SIZE] =
            {
                    {1.f},
                    {0.25f,    0.5f,      0.25f},
                    {0.0625f,  0.25f,     0.375f,   0.25f,    0.0625f},
                    {0.03125f, 0.109375f, 0.21875f, 0.28125f, 0.21875f, 0.109375f, 0.03125f}
            };

    const float *fixed_kernel = ksize % 2 == 1 && ksize <= SMALL_GAUSSIAN_SIZE && sigma <= 0 ?
                                small_gaussian_tab[ksize >> 1] : nullptr;

    Mat kernel = Mat(ksize, 1, ktype);
    auto *cd = kernel.ptr<double>();

    double sigmaX = sigma > 0 ? sigma : ((ksize - 1) * 0.5 - 1) * 0.3 + 0.8;
    double scale2X = -0.5 / (sigmaX * sigmaX);
    double sum = 0;

    int radius = ksize / 2;
    int i;
    for (i = 0; i < ksize; i++) {
        double x = i - radius;
        double t = fixed_kernel ? (double) fixed_kernel[i] : std::exp(scale2X * x * x);

        cd[i] = t;
        sum += cd[i];
    }

    sum = 1. / sum;
    for (i = 0; i < ksize; i++) {
        cd[i] *= sum;
    }

    return kernel;
}

void GaussianFilter::Conv2d(Mat src, Mat &dst, Mat filter) {
    int filter_h = filter.rows;
    int filter_w = filter.cols;

    int radius_y = filter_h / 2;
    int radius_x = filter_w / 2;

    int h = src.rows;
    int w = src.cols;

    double temp;
    int target_x;
    int target_y;
    bool flag;
    for (int i = 0; i < h; i++) {
        auto *data = dst.ptr<uchar>(i);
        for (int j = 0; j < w; j++) {
            temp = 0;
            for (int k = 0; k < filter_h; k++) {
                for (int l = 0; l < filter_w; l++) {
                    target_x = j - radius_x + l;
                    target_y = i - radius_y + k;

                    flag = target_x >= 0 and target_x < h and target_y >= 0 and target_y < w;
                    if (flag) {
                        auto *src_data = src.ptr<uchar>(target_y);
                        auto *filter_data = filter.ptr<double>(k);
                        temp += (int) src_data[target_x] * filter_data[l];
                    }
                }
            }
            data[j] = (uchar) round(temp);
        }
    }
}

测试代码如下：

#include <sys/time.h>
#include <iostream>
#include <opencv2/opencv.hpp>
#include "GaussianFilter.h"

using namespace std;
using namespace cv;

string getMillisecond() {
    struct timeval tv;
    gettimeofday(&tv, NULL);

    long int ms = tv.tv_sec * 1000 + tv.tv_usec / 1000;
    return to_string(ms);
}

void opencv_gauss() {
    Mat img = imread("lena.jpg");
    if (img.empty()) {
        std::cout << "error" << std::endl;
        exit(0);
    }

    Mat dst = img.clone();
    GaussianBlur(img, dst, Size(5, 5), 1, 1);

    imshow("img", img);
    imshow("gauss", dst);
    waitKey(0);
}


void custom_gauss(int ksize = 3, double sigma = 1.0) {
    Mat img = imread("lena.jpg");

    GaussianFilter gaussianFilter;

    Mat dst1 = img.clone();
    long int start = stol(getMillisecond());
    gaussianFilter.GaussianBlur(img, dst1, Size(ksize, ksize), sigma);
    long int end = stol(getMillisecond());
    cout << end - start << endl;

    Mat dst2 = img.clone();
    start = stol(getMillisecond());
    GaussianBlur(img, dst2, Size(ksize, ksize), sigma);
    end = stol(getMillisecond());
    cout << end - start << endl;

    imshow("img", img);
    imshow("dst1", dst1);
    imshow("dst2", dst2);
    waitKey(0);
}

int main() {
    custom_gauss(3, 0.85);

    return 0;

CMakeLists.txt内容如下：

cmake_minimum_required(VERSION 3.13)
project(opencv_project)

set(CMAKE_CXX_STANDARD 11)

#set(CMAKE_PREFIX_PATH /home/zj/opencv/opencv-4.0.1/install)
find_package( OpenCV REQUIRED )
MESSAGE("OpenCV version: ${OpenCV_VERSION}")
include_directories( ${OpenCV_INCLUDE_DIRS} )

add_executable(opencv_project main.cpp GaussianFilter.cpp GaussianFilter.h)

target_link_libraries( opencv_project ${OpenCV_LIBS} )

测试结果如下（单位：ms）：

	OpenCV	自定义	优化
3x3	4	67	64
5x5	6	182	94

进一步优化方向是多线程、编译优化、模板查表等