Nesterov加速梯度

发表于 更新于 分类于 阅读次数：47
本文字数： 1.7k 阅读时长 ≈ 3 分钟

Nesterov加速梯度（Nesterov's Accelerated Gradient，简称NAG）是梯度下降的一种优化方法，其收敛速度比动量更新方法更快，收敛曲线更加稳定

实现公式

NAG计算公式参考On the importance of initialization and momentum in deep learning

wt−1ahead=wt−1+μvt−1vt=μvt−1−lr▽f(wt−1ahead)wt=wt−1+vt

其实现和经典动量的区别在于 NAG计算的是当前权重加上累积速度后的梯度

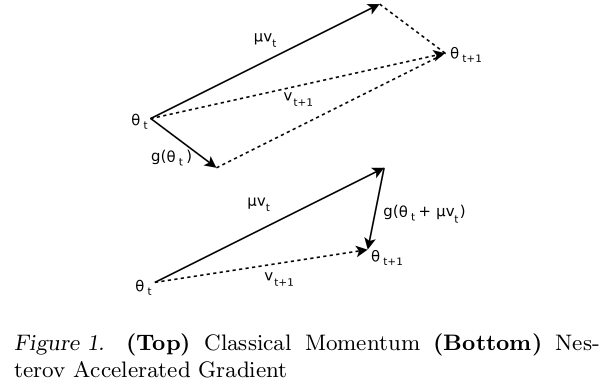
替换公式

实际使用过程中使用替换公式，参考Neural Networks Part 3: Learning and Evaluation

wt=wt−1+vt⇒wt+μvt+μvt−1=wt−1+vt+μvt+μvt−1⇒wtahead+μvt−1=wt−1ahead+(1+μ)vt⇒wtahead=wt−1ahead+(1+μ)vt−μvt−1

所以替换公式为

vt=μvt−1−lr▽f(wt−1ahead)wtahead=wt−1ahead+(1+μ)vt−μvt−1

⇒

vt=μvt−1−lr▽f(wt−1)wt=wt−1+(1+μ)vt−μvt−1

将使用的权重向量替换为权重向量加上累积速度后的权重值

numpy测试

参考：动量更新

原始公式实现

NAG实现代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def sgd_nesterov(x_start, lr, epochs=100, mu=0.5):
    dots = [x_start]

    x = x_start.copy()
    v = np.zeros((2))
    for i in range(epochs):
        x_ahead = x + mu * v
        grad = gradient(x_ahead)
        v = mu * v - lr * grad
        x += v
        dots.append(x.copy())
        if abs(np.sum(grad)) < 1e-6:
            break
    return np.array(dots)

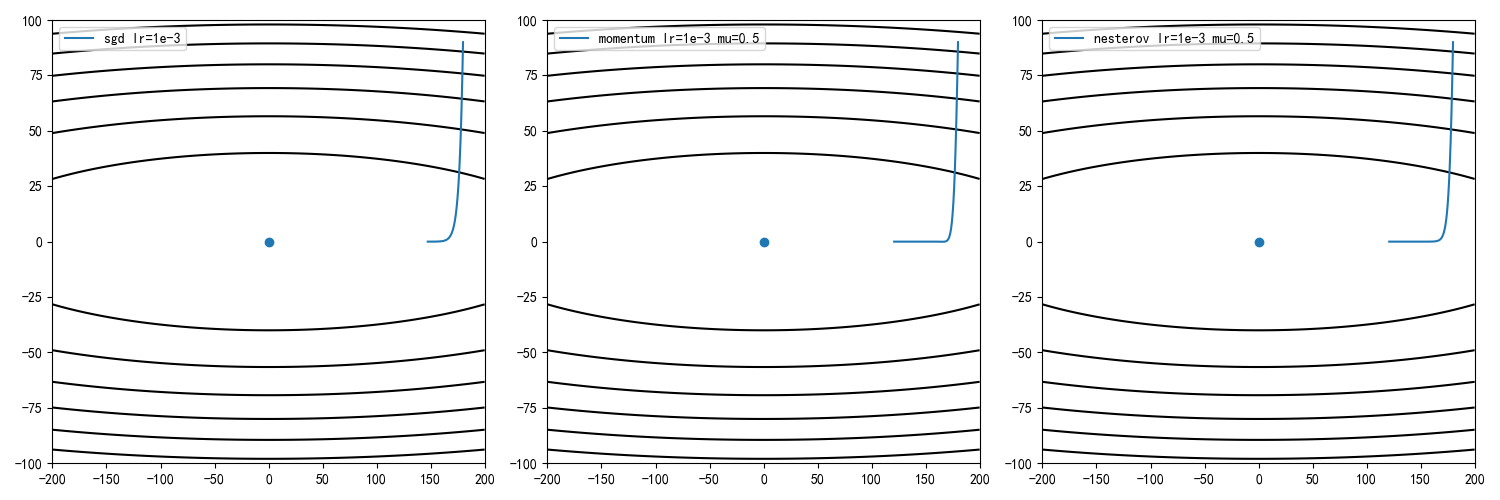
SGD vs CM vs NAG

学习率1e-3，动量因子0.5，迭代100次结果

学习率1e-2，动量因子0.5，迭代100次结果

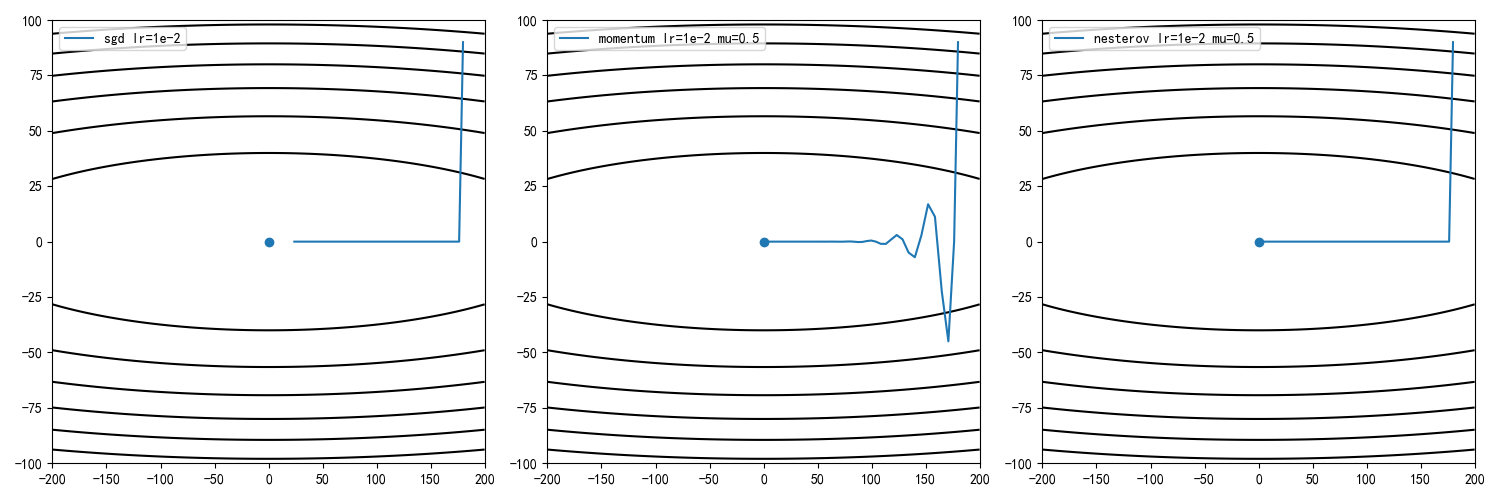
经典动量和NAG方法的收敛速度均比标准梯度下降更快

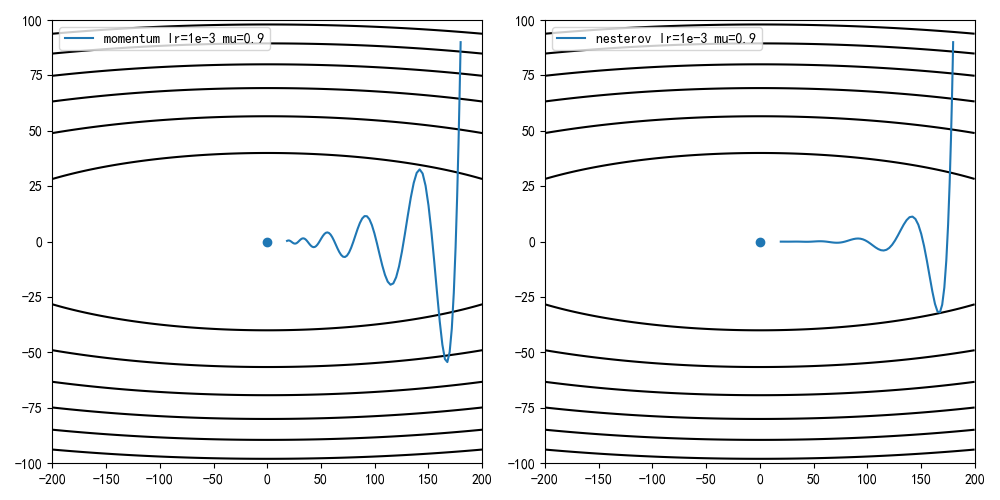
CM vs NAG

学习率1e-3，动量因子0.9，迭代100次结果

学习率1e-2，动量因子0.9，迭代100次结果

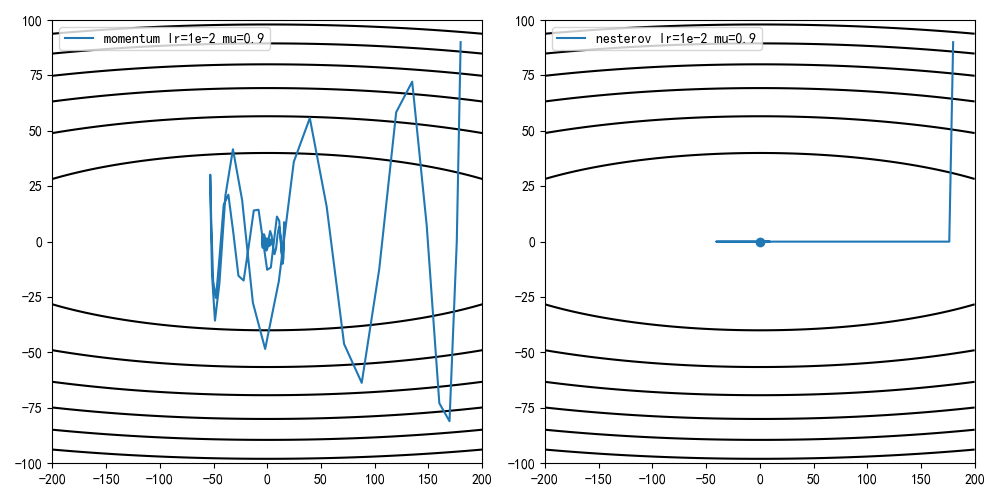
NAG方法的收敛曲线比经典动量方法更稳定

替换公式实现

替换公式实现代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def sgd_nesterov_v2(x_start, lr, epochs=100, mu=0.5):
    dots = [x_start]

    x = x_start.copy()
    v = 0
    for i in range(epochs):
        grad = gradient(x)
        v_prev = v
        v = mu * v - lr * grad
        x += (1 + mu) * v - mu * v_prev
        dots.append(x.copy())
        if abs(np.sum(grad)) < 1e-6:
            break
    return np.array(dots)

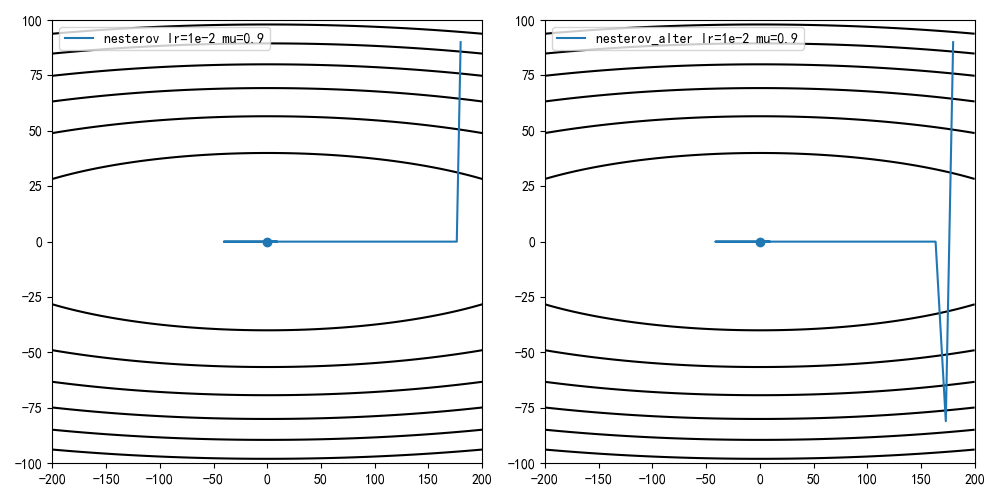
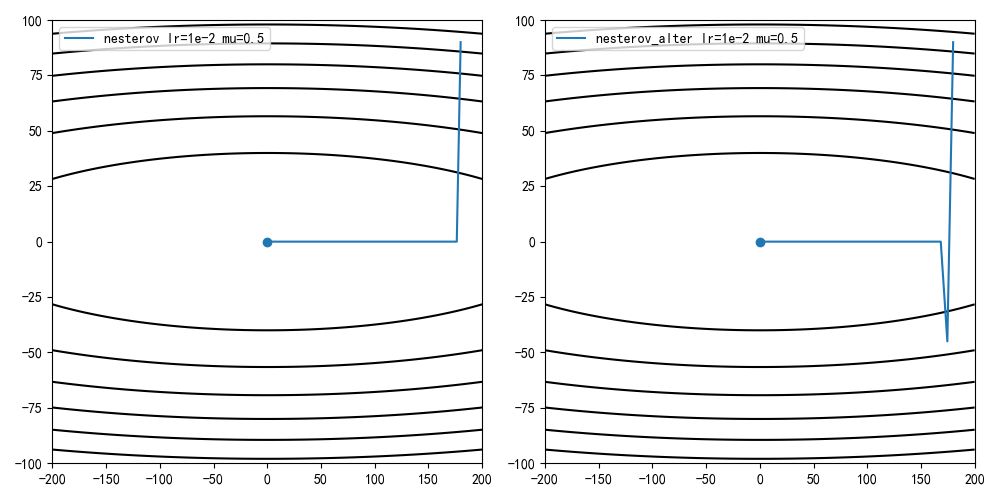
NAG vs NAG_alter

学习率1e-3，动量因子0.9，迭代100次结果

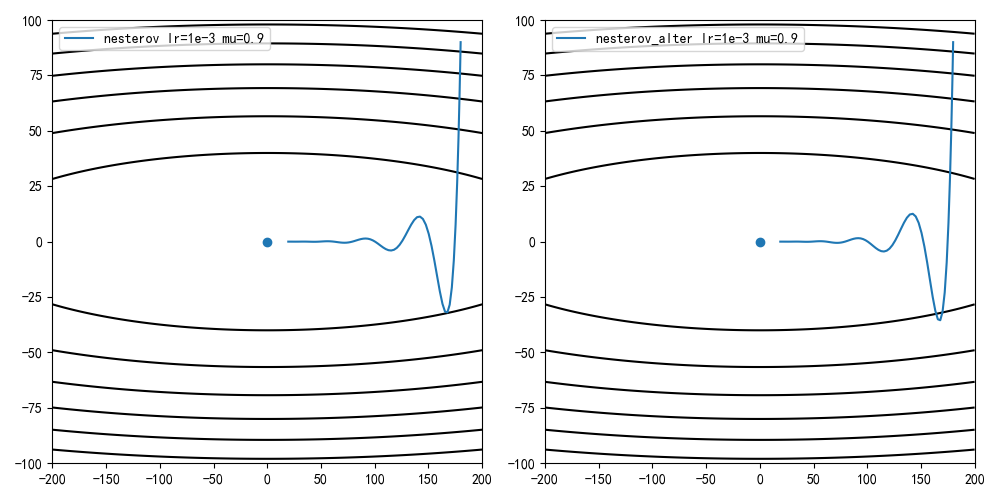
学习率1e-2，动量因子0.9，迭代100次结果

学习率1e-2，动量因子0.5，迭代100次结果

相关资料

Nesterov Accelerated Gradient and Momentum

比Momentum更快：揭开Nesterov Accelerated Gradient的真面目