从numpy到pytorch实现线性回归

发表于 更新于 分类于 ， ， ， ， ，
本文字数： 8.1k 阅读时长 ≈ 15 分钟

参考：

Linear Regression and Gradient Descent from scratch in PyTorch

PyTorch进阶之路（二）：如何实现线性回归

线性回归

特征缩放

首先利用numpy实现梯度下降解决多变量线性回归问题，然后逐步将操作转换成pytorch

实现步骤如下：

  1. 加载训练数据
  2. 初始化权重
  3. 计算预测结果
  4. 计算损失函数
  5. 梯度更新
  6. 重复3-5步，直到完成迭代次数
  7. 绘制损失图

多变量线性回归测试数据参考ex1data2.txt

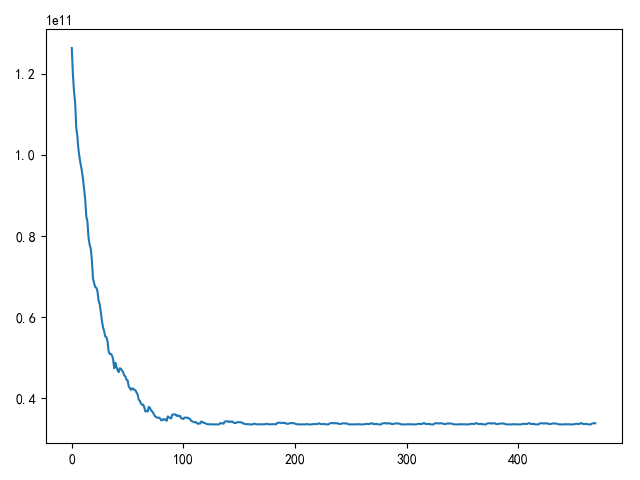
numpy实现随机梯度下降

参考：梯度下降

随机梯度下降实现如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
# -*- coding: utf-8 -*-

# @Author  : zj

"""
梯度下降法计算线性回归问题
"""

import matplotlib.pyplot as plt
import numpy as np


def load_ex1_multi_data():
    """
    加载多变量数据
    """
    path = '../data/coursera2.txt'
    datas = []
    with open(path, 'r') as f:
        lines = f.readlines()
        for line in lines:
            datas.append(line.strip().split(','))
    data_arr = np.array(datas)
    data_arr = data_arr.astype(np.float)

    X = data_arr[:, :2]
    Y = data_arr[:, 2]
    return X, Y


def draw_loss(loss_list):
    """
    绘制损失函数值
    """
    fig = plt.figure()
    plt.plot(loss_list)

    plt.show()


def init_weight(size):
    """
    初始化权重，使用均值为0,方差为1的标准正态分布
    """
    return np.random.normal(loc=0.0, scale=1.0, size=size)


def compute_loss(w, x, y):
    """
    计算损失值
    """
    n = y.shape[0]
    return (x.dot(w) - y).T.dot(x.dot(w) - y) / n


def using_stochastic_gradient_descent():
    """
    随机梯度下降
    """
    x, y = load_ex1_multi_data()
    extend_x = np.insert(x, 0, values=np.ones(x.shape[0]), axis=1)
    w = init_weight(extend_x.shape[1])
    # print(w)
    print(w.shape)

    # 打乱数据
    np.random.shuffle(extend_x)
    print(extend_x.shape)
    print(y.shape)

    n = y.shape[0]
    epoches = 10
    alpha = 1e-8
    loss_list = []
    for i in range(epoches):
        for j in range(n):
            temp = w - alpha * (extend_x[j].dot(w) - y[j]) * extend_x[j].T / 2
            w = temp
            loss_list.append(compute_loss(w, extend_x, y))
    draw_loss(loss_list)


if __name__ == '__main__':
    using_stochastic_gradient_descent()

pytorch实现批量梯度下降

pytorch使用tensor作为数据保存结构，使用函数from_numpy可以将numpy array数组转换成tensor类型

1
torch.from_numpy(X), torch.from_numpy(Y)

使用torch.randn可以生成符合标准正态分布的随机数组，用于生成权重和偏置值

1
torch.randn(h, 1, requires_grad=True, dtype=torch.double), torch.randn(1, requires_grad=True,                                                                                  dtype=torch.double)

pytorch内置了autograd包，计算预测结果和损失函数后，调用函数backward()就能够自动计算出梯度

首先需要开启权重和偏置值的梯度开关，然后在调用函数后进行梯度更新

1
2
3
4
5
with torch.no_grad():
      w -= w.grad * lr
      b -= b.grad * lr
      w.grad.zero_()
      b.grad.zero_()

使用torch.no_grad能够保证梯度更新过程中不再计算梯度值，计算完成后需要将梯度归零，避免下次叠加

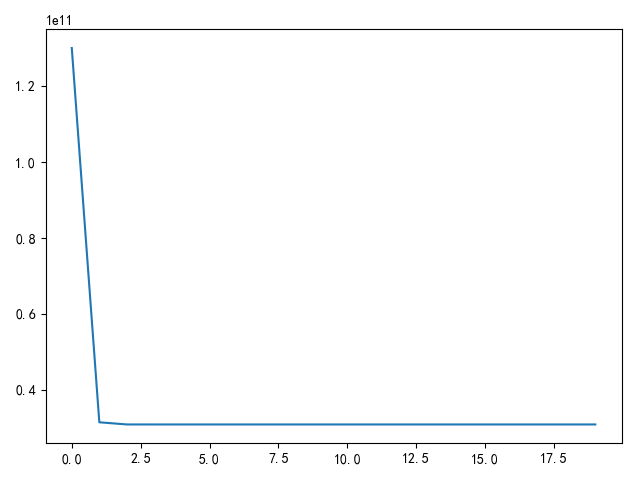
使用pytorch实现批量梯度下降计算多变量线性回归问题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
# -*- coding: utf-8 -*-

# @Author  : zj

"""
梯度下降法计算线性回归问题
"""

import matplotlib.pyplot as plt
import numpy as np
import torch


def load_ex1_multi_data():
    """
    加载多变量数据
    """
    path = '../data/coursera2.txt'
    datas = []
    with open(path, 'r') as f:
        lines = f.readlines()
        for line in lines:
            datas.append(line.strip().split(','))
    data_arr = np.array(datas)
    data_arr = data_arr.astype(np.float)

    X = data_arr[:, :2]
    Y = data_arr[:, 2]

    return torch.from_numpy(X), torch.from_numpy(Y)


def init_weight(h):
    """
    初始化权重，使用均值为0,方差为1的标准正态分布
    """
    return torch.randn(h, 1, requires_grad=True, dtype=torch.double), torch.randn(1, requires_grad=True,
                                                                                  dtype=torch.double)


def predict_result(w, b, x):
    """
    预测结果
    """
    return x.mm(w) + b


def compute_loss(w, b, x, y):
    """
    计算损失值 MSE
    """
    diff = y - predict_result(w, b, x)
    return torch.sum(diff * diff) / diff.numel()


def draw_loss(loss_list):
    """
    绘制损失函数值
    """
    fig = plt.figure()
    plt.plot(loss_list)

    plt.show()


def using_batch_gradient_descent():
    """
    批量梯度下降
    """
    x, y = load_ex1_multi_data()
    w, b = init_weight(x.shape[1])

    epoches = 20
    lr = 1e-7
    loss_list = []
    for i in range(epoches):
        # 计算损失值
        loss = compute_loss(w, b, x, y)
        # 保存损失值
        loss_list.append(loss)
        # 反向更新
        loss.backward()
        # 梯度更新
        with torch.no_grad():
            w -= w.grad * lr
            b -= b.grad * lr
            w.grad.zero_()
            b.grad.zero_()
    draw_loss(loss_list)


if __name__ == '__main__':
    using_batch_gradient_descent()

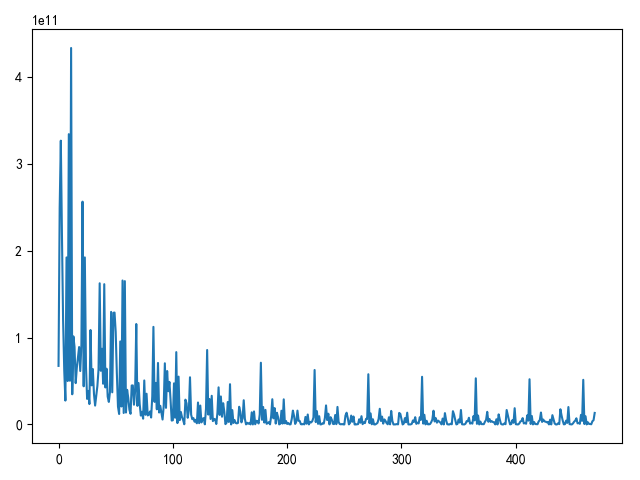
pytorch实现随机梯度下降

pytorch提供了许多类和函数用于计算，下面实现随机梯度下降解决多变量线性回归

首先在numpy数组转换成pytorch tensor类型前先打乱数据

1
2
3
4
5
# 打乱数据
indexs = np.arange(X.shape[0])
np.random.shuffle(indexs)
X = X[indexs]
Y = Y[indexs]

pytorch.nn包提供了类Linear用于线性计算

1
2
3
4
5
6
7
# 定义线性模型
model = nn.Linear(x.size()[1], 1)
# 获取初始权重和偏置值
w = model.weight
b = model.bias
# 计算预测结果，计算损失值
diff = y - model(x)

pytorch.nn.function包提供了函数mse_loss用于计算均方误差

也可以使用包装类nn.MSELoss

1
2
3
4
5
6
7
8
9
# 损失函数
loss_fn = F.mse_loss
# 计算损失值
loss = loss_fn(model(x), y)
# 或者
# 损失函数
criterion = nn.MSELoss()
# 计算损失值
loss = criterion(model(x), y)

pytorch.optim提供了类SGD用于计算随机梯度下降

1
2
3
4
5
6
7
8
# 定义优化器
optimizer = optim.SGD(model.parameters(), lr=2e-7, momentum=0.9)
# 清空梯度
optimizer.zero_grad()
# 计算梯度
loss.backward()
# 更新
optimizer.step()

实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
# -*- coding: utf-8 -*-

# @Author  : zj

"""
梯度下降法计算线性回归问题
"""

import matplotlib.pyplot as plt
import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim


def load_ex1_multi_data():
    """
    加载多变量数据
    """
    path = '../data/coursera2.txt'
    datas = []
    with open(path, 'r') as f:
        lines = f.readlines()
        for line in lines:
            datas.append(line.strip().split(','))
    data_arr = np.array(datas)
    data_arr = data_arr.astype(np.float)

    X = data_arr[:, :2]
    Y = data_arr[:, 2]
    
    # 打乱数据
    indexs = np.arange(X.shape[0])
    np.random.shuffle(indexs)
    X = X[indexs]
    Y = Y[indexs]

    return torch.from_numpy(X).float(), torch.from_numpy(Y).float()


def draw_loss(loss_list):
    """
    绘制损失函数值
    """
    fig = plt.figure()
    plt.plot(loss_list)

    plt.show()


def using_stochastic_gradient_descent():
    """
    随机梯度下降
    """
    x, y = load_ex1_multi_data()

    # 定义线性模型
    model = nn.Linear(x.size()[1], 1)
    # 获取初始权重和偏置值
    w = model.weight
    b = model.bias

    # 损失函数
    criterion = nn.MSELoss()
    # 定义优化器
    optimizer = optim.SGD(model.parameters(), lr=1e-10, momentum=0.9)

    epoches = 10
    loss_list = []
    for i in range(epoches):
        for j, item in enumerate(x, 0):
            # 计算损失值
            loss = criterion(model(item), y[j])
            # 清空梯度
            optimizer.zero_grad()
            # 计算梯度
            loss.backward()
            # 更新
            optimizer.step()
            # 保存损失值
            loss_list.append(loss)
    draw_loss(loss_list)


if __name__ == '__main__':
    using_stochastic_gradient_descent()

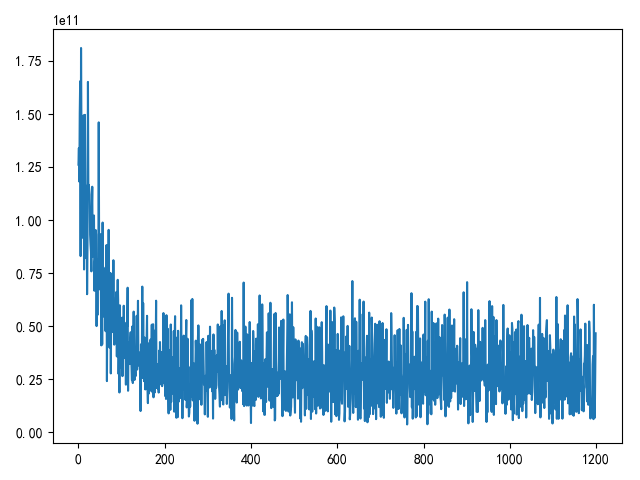
pytorch实现小批量梯度下降

实际训练过程中最常使用的梯度下降方法是小批量梯度下降，

pytorch提供了类torch.utils.data.TensorDataset以及torch.utils.data.DataLoader来实现数据的加载、打乱和批量化

1
2
3
4
5
6
7
batch_size = 8
data_ts = TensorDataset(x, y)
data_loader = DataLoader(data_ts, batch_size=batch_size, shuffle=True)
for j, item in enumerate(data_loader, 0):
    inputs, targets = item
    # 计算损失值
    loss = criterion(model(inputs), targets)

实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
# -*- coding: utf-8 -*-

# @Author  : zj

"""
梯度下降法计算线性回归问题
"""

import matplotlib.pyplot as plt
import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torch.utils.data import TensorDataset
from torch.utils.data import DataLoader


def load_ex1_multi_data():
    """
    加载多变量数据
    """
    path = '../data/coursera2.txt'
    datas = []
    with open(path, 'r') as f:
        lines = f.readlines()
        for line in lines:
            datas.append(line.strip().split(','))
    data_arr = np.array(datas)
    data_arr = data_arr.astype(np.float)

    X = data_arr[:, :2]
    Y = data_arr[:, 2]

    return torch.from_numpy(X).float(), torch.from_numpy(Y).float()


def draw_loss(loss_list):
    """
    绘制损失函数值
    """
    fig = plt.figure()
    plt.plot(loss_list)

    plt.show()


def using_small_batch_gradient_descent():
    """
    小批量梯度下降
    """
    x, y = load_ex1_multi_data()

    batch_size = 8
    data_ts = TensorDataset(x, y)
    data_loader = DataLoader(data_ts, batch_size=batch_size, shuffle=True)

    # 定义线性模型
    model = nn.Linear(x.size()[1], 1)
    # 获取初始权重和偏置值
    w = model.weight
    b = model.bias

    # 损失函数
    criterion = nn.MSELoss()
    # 定义优化器
    optimizer = optim.SGD(model.parameters(), lr=1e-10, momentum=0.9)

    epoches = 200
    loss_list = []
    for i in range(epoches):
        for j, item in enumerate(data_loader, 0):
            # print(item)
            inputs, targets = item
            # 计算损失值
            loss = criterion(model(inputs), targets)
            # 清空梯度
            optimizer.zero_grad()
            # 计算梯度
            loss.backward()
            # 更新
            optimizer.step()
            # 保存损失值
            loss_list.append(loss)
    draw_loss(loss_list)


if __name__ == '__main__':
    using_small_batch_gradient_descent()

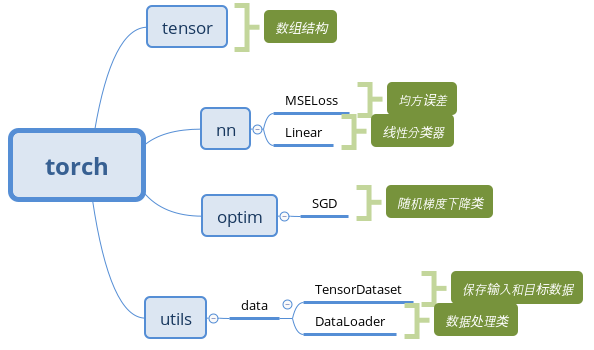
小结

pytorch使用到的类库如下所示