数据结构-图3

发表于 更新于 分类于
本文字数： 3.4k 阅读时长 ≈ 6 分钟

学习路径如下：

  1. 图的基本定义
  2. 顶点/边/图的关系
  3. 图的存储结构（本文学习内容）
  4. 深度/广度优先遍历
  5. 最小生成树

完整工程：zjZSTU/GraphLib

概述

有5种图的存储结构：

  1. 邻接矩阵
  2. 邻接表
  3. 十字链表
  4. 邻接多重表
  5. 边集数组

其中常用的存储结构是邻接矩阵和邻接表

邻接矩阵

图由两部分组成：顶点集+边集，分别存储这两部分有利于后续的操作

图的邻接矩阵（adjacency matrix）存储方式是用两个数组来表示图。一个一维数组存储图中顶点信息，一个二维数组（称为邻接矩阵）存储图中的边或弧信息

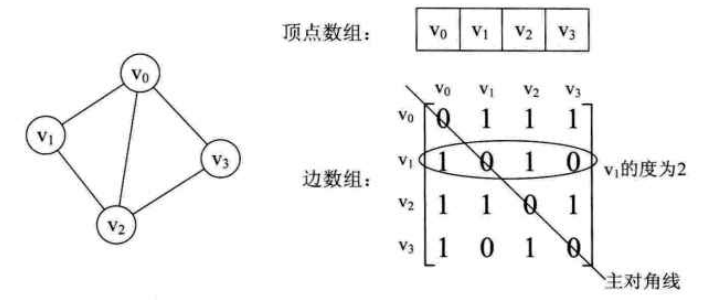
设图\(G\)中有两个顶点，则邻接矩阵是一个\(n\times n\)的方阵，定义为：

\[ arc[i][j] = \left\{\begin{matrix} 1 & 若(v_{i}, v_{j})\subseteq E或<v_{i}, v_{j}>\subseteq E\\ 0 & 反之 \end{matrix}\right. \]

对于有权图，修改邻接矩阵指定位置的值即可，如下所示：

\[ arc[i][j] = \left\{\begin{matrix} 1 & 若(v_{i}, v_{j})\subseteq E或<v_{i}, v_{j}>\subseteq E\\ 0 & 若i==j\\ \infty & 反之 \end{matrix}\right. \]

使用\(\infty\)表示两顶点之间没有连接

C++实现

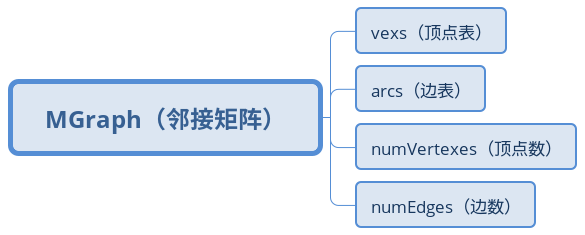
定义邻接矩阵

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include <iostream>
#include <array>

// 假定最大顶点个数
#define MAXVEX 100
// 假定最大边集个数
#define MAXEDGE 100
// 模拟无穷大
#define GINFINITY 63335


// 顶点数据类型
typedef std::string VertexType;
// 边权值类型
typedef int EdgeType;

// 邻接矩阵存储结构
typedef struct {
    // 顶点表
    std::array<VertexType, MAXVEX> vexs;
    // 边表
    std::array<std::array<EdgeType, MAXVEX>, MAXVEX> arcs;
    int numVertexes, numEdges;
} MGraph;

创建邻接矩阵

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
void Undigraph::CreateMGraph(MGraph *G) {
    int i, j, k, w;

    cout << "输入顶点数: ";
    cin >> G->numVertexes;
    cout << "输入边集数: ";
    cin >> G->numEdges;

    cout << "输入顶点信息：" << endl;
    for (i = 0; i < G->numVertexes; i++) {
        cin >> G->vexs[i];
    }

    // 初始化边集二维数组
    for (i = 0; i < G->numVertexes; i++) {
        for (j = 0; j < G->numVertexes; j++) {
            if (i == j)
                G->arcs[i][j] = 0;
            else
                G->arcs[i][j] = GINFINITY;
        }
    }

    cout << "输入边信息" << endl;
    for (k = 0; k < G->numEdges; k++) {
        cout << "输入第" << k << "条边的上标、下标和权值: ";
        cin >> i >> j >> w;
        G->arcs[i][j] = w;
        G->arcs[j][i] = w;
    }
}

邻接表

邻接表（adjacency list）同样实现了顶点集和边集的分离，如下所示：

  1. 顶点集用一个一维数组存储（也可使用单链表存储），每个数据元素对象包含指向第一个邻接点的指针
  2. 每个顶点使用单链表存储邻接点信息，同时包含指向下一个邻接点的指针

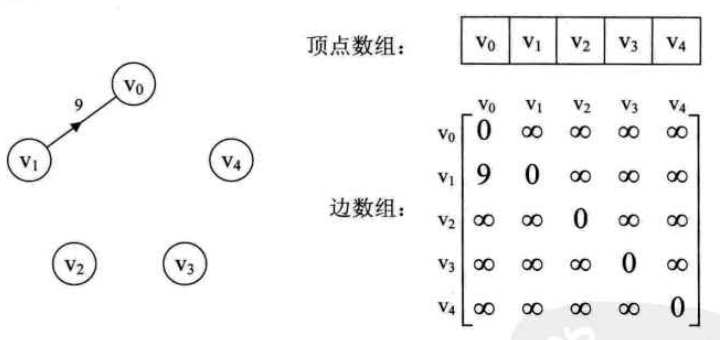
c++实现

顶点对象有两个域：data和firstedge。data存储顶点信息，firstedge指向第一个临界点

边对象有两个域：adjvex和next。adjvex存储该邻接点在顶点表中的下标，next指向下一个邻接点

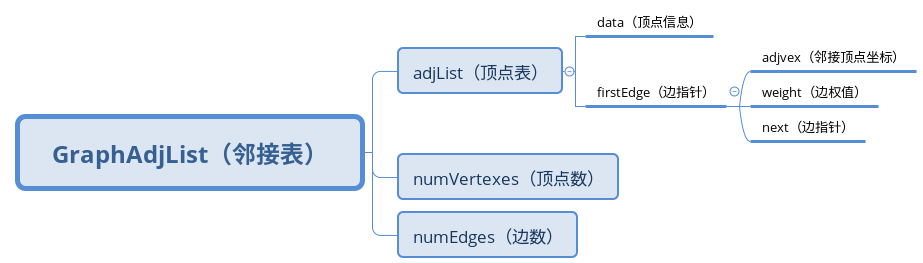
定义邻接表：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
// 边表结点
typedef struct EdgeNode {
    // 邻接点域，存储该顶点对应的坐标
    int adjvex;
    // 存储权值
    EdgeType weight;
    struct EdgeNode *next;
} EdgeNode;

// 顶点表结点
typedef struct VertexNode {
    VertexType data;
    EdgeNode *firstEdge;
} VertextNode;

// 邻接表
typedef struct {
    // 顶点集数组
    std::array<VertextNode, MAXVEX> adjList;
    // 顶点集和边集大小
    int numVertexes, numEdges;
} GraphAdjList;

创建邻接表：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
void Undigraph::CreateGraphAdjList(GraphAdjList *G) {
    int i, j, k, w;
    EdgeNode *e;

    cout << "输入顶点数: ";
    cin >> G->numVertexes;
    cout << "输入边集数: ";
    cin >> G->numEdges;

    cout << "输入顶点信息：" << endl;
    for (i = 0; i < G->numVertexes; i++) {
        cin >> G->adjList[i].data;
        G->adjList[i].firstEdge = nullptr;
    }

    cout << "输入边信息" << endl;
    for (k = 0; k < G->numEdges; k++) {
        cout << "输入第" << k << "条边的上标、下标和权值: ";
        cin >> i >> j >> w;
        // 申请内存空间
        e = (EdgeNode *) malloc(sizeof(EdgeNode));
        e->adjvex = j;
        e->weight = w;
        // 头插法
        e->next = G->adjList[i].firstEdge;
        G->adjList[i].firstEdge = e;

        // 无向图的边表对称
        e = (EdgeNode *) malloc(sizeof(EdgeNode));
        e->adjvex = i;
        e->weight = w;
        // 头插法
        e->next = G->adjList[j].firstEdge;
        G->adjList[j].firstEdge = e;
    }
}

小结

假定图有\(n\)个顶点和\(e\)条边，那么

  • 创建邻接矩阵的时间复杂度为\(O(n^{2}+e)\)，创建邻接表的时间复杂度为\(O(n+e)\)
  • 邻接矩阵的使用极大的浪费存储空间，但有利于数据查询、修改、增添和删除操作
  • 邻接表的使用有利于避免浪费存储空间，但是提高了数据查询、修改、增添和删除操作的复杂度

相关阅读

  • 《大话数据结构》第7章 图