学习路径如下:
图的基本定义 顶点/边/图的关系 图的存储结构 深度/广度优先遍历 (本文学习内容 )最小生成树 完整工程:zjZSTU/graph_algorithm
图的遍历 从图中某一顶点出发访遍图中其余顶点,且使每一个顶点仅被访问一次,这一过程称为图的遍历(traversing graph)
深度优先遍历 深度优先遍历(depth first search,DFS):
从图中某个顶点
深度优先 指的是每次选择当前访问顶点的邻接点集中未被访问过的点作为下一个访问的点创建一维数组visited保存已访问顶点 创建一维数组ordered保存访问次序 可使用递归方式进行深度优先遍历的实现 c++实现 分别实现邻接矩阵和邻接表的深度优先遍历,使用递归方式实现
邻接矩阵 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 bool visited[MAXVEX];int ordered[MAXVEX];int *Undigraph::DFSTraverse(MGraph G) { int i; for (i = 0 ; i < G.numVertexes; i++) { visited[i] = false ; } int index = 0 ; for (i = 0 ; i < G.numVertexes; i++) { if (!visited[i]) { DFS(G, i, &index ); } } return ordered; } void Undigraph::DFS(MGraph G, int up, int *index ) { int j; visited[up] = true ; ordered[*index ] = up; *index += 1 ; for (j = 0 ; j < G.numVertexes; j++) { if (up != j and G.arcs[up][j] != GINFINITY and !visited[j]) { DFS(G, j, index ); } } }
邻接表 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 int *Undigraph::DFSTraverse(GraphAdjList G) { int i; for (i = 0 ; i < G.numVertexes; i++) { visited[i] = false ; } int index = 0 ; for (i = 0 ; i < G.numVertexes; i++) { if (!visited[i]) { DFS(G, i, &index ); } } return ordered; } void Undigraph::DFS(GraphAdjList G, int up, int *index ) { visited[up] = true ; ordered[*index ] = up; *index += 1 ; EdgeNode *e = G.adjList[up].firstEdge; while (e != nullptr) { if (!visited[e->adjvex]) { DFS(G, e->adjvex, index ); } e = e->next ; } }
广度优先遍历 广度优先遍历(breadth first search,BFS):
从图中某个顶点
广度优先 指的是每次选择和当前访问顶点同属一层的未被访问过的点作为下一个访问点创建一维数组visited保存已访问顶点 创建一维数组ordered保存访问次序 可使用队列结构进行广度优先遍历的实现
c++实现 分别使用邻接矩阵和邻接表实现广度优先遍历,采用队列方式
邻接矩阵 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 bool visited[MAXVEX] ;int ordered[MAXVEX] ;int *Undigraph::BFSTraverse(MGraph G) { int i, j, k; int index = 0 ; std::queue<int > q; for (i = 0 ; i < G . visited[i ] = false ; } for (i = 0 ; i < G . if (!visited[i ] ) { visited[i ] = true ; ordered[index ] = i; index++; q.push(i); while (!q.empty() ) { k = q.front() ; q.pop() ; for (j = 0 ; j < G . if (k != j and G .[k ] [j ] != GINFINITY and !visited[j ] ) { visited[j ] = true ; ordered[index ] = j; index++; q.push(j); } } } } } return ordered; }
邻接表 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 int *Undigraph::BFSTraverse(GraphAdjList G) { int i, k; EdgeNode *e ; int index = 0 ; std::queue<int > q; for (i = 0 ; i < G.numVertexes; i++) { visited[i] = false; } for (i = 0 ; i < G.numVertexes; i++) { if (!visited[i]) { visited[i] = true; ordered [index] = i; index++; q.push(i); while (!q.empty()) { k = q.front(); q.pop(); e = G.adjList[k].firstEdge; while (e != nullptr) { if (!visited[e ->adjvex]) { visited[e ->adjvex] = true; ordered [index] = e ->adjvex; index++; q.push(e ->adjvex); } e = e ->next; } } } } return ordered ; }
小结 对于
如果使用邻接矩阵作为存储结构,需要遍历顶点集,每次遍历单个顶点的边集时同样需要遍历二维邻接矩阵的每行(或每列),所以时间复杂度为 如果使用邻接表作为存储结构,同样需要遍历顶点集,每次遍历单个顶点的边集时仅取决于边集的大小,极端情况下,仅需一个顶点就能遍历所有边集,所以时间复杂度为 所以对于稀疏图而言,使用邻接表的效率远远大于邻接矩阵
深度优先遍历和广度优先遍历的时间复杂度相同,使用过程中依据具体情况分析
深度优先更适合目标比较明确,以找到目标为主要目的的情况。有点像学习/开发过程后期,如果有明确研究目标,那就不断细分到想要的方向进行学习/研究 广度优先更适合在不断扩大遍历范围时找到相对最优解的情况。有点像学习/开发过程初期,先广泛的收集资料和数据,力图发现最好的学习/研究目标 相关阅读 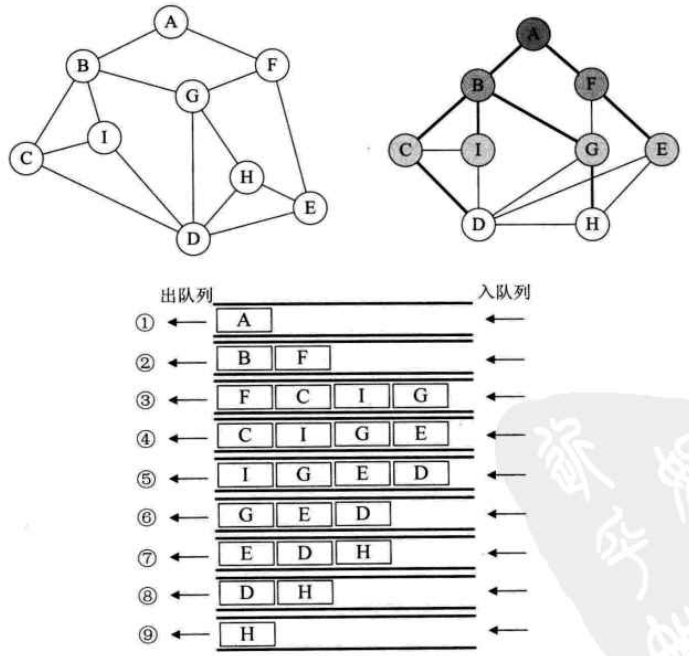
未找到相关的 Issues 进行评论
请联系 @zjykzj 初始化创建